|
exercice
1
|
cabine
d'ascenceur
|
|
Une cabine d'ascenseur de masse M=300 kg
transporte une charge de masse m=200kg. le cable
exerce sur la cabine une force F d'intensité
5900N. g=10ms-2. Il est alors possible
que:
la cabine descende avec une
accélération de -1,8
ms-2.
la cabine monte avec une
accélérationde 0,55
ms-2.
la cabine monte à vitesse constante
la cabine descende à vitesse
constante
la cabine soit immobile
|
|
|
corrigé
|
|
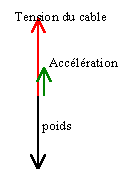
|
tan(a)=1,16 /2
a=30°
|
Suivant un axe
vertical dirigé vers le haut la seconde loi
de Newton s'écrit:
-(M+m)g+F=(M+m)a
a=(-5000+5900)/
500=1,8
ms-2.
montée avec
a=1,8ms-2
.descente avec a=
-1,8ms-2
|
|
|
|
exercice
2
|
mouvement
sur un plan horizontal
|
|
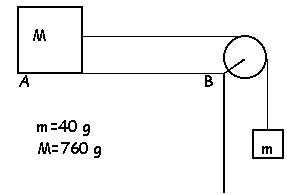
les frottements sont négligeables.
g=10 m
s-2.
|
temps(s)
|
0,6
|
1
|
1,8
|
|
position (cm)
|
17,6
|
39,6
|
110
|
|
vitesse (ms-1)
|
0,45
|
0,65
|
1,05
|
|
Ec de la masse M
(millijoule)
|
77
|
161
|
419
|
(répondre vrai
ou faux)
- l'accélération
est constante et sa valeur est 0,4 m
s-2.
- le mouvement est
uniformément
accéléré.
- la vitesse à l'
instant t=0 est nulle.
- la tension du fil est
0,4 N.
|
|
|
|
corrigé
|
|
|
|
|
faux
la valeur de l'accélération est 0,5 m
s-2.
|
DV
|
0,2
|
0,4
|
|
Dt
|
0,4
|
0,8
|
|
a
|
0,2/0,4=0,5
|
0,4/0,8=0,5
|
vrai
le mouvement est rectiligne et la valeur de
l'accélérarion est constante.
faux
la vitesse augmente de 0,5 m s-1
à chaque seconde.
à t=0 la vitesse
initiale est donc:
0,65-0,5=0,15
m
s-1.
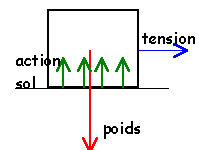
faux
seule la tension effectue un travail
mécanique, les autres forces sont
perpendiculaires à la vitesse. Entre les
instants t= 0,6 et t=1,8 s :
variation d'énergie
cinétique de M:
0,342 J
travail de la tension au
cours du déplacement 1,1-0,176=0,924
m
th
de l'énergie cinétique
tension*0,924=0,342
T=0,37
N
|
|
|
|
exercice
3
|
glissière
circulaire -chute- vitesse-
accélération
|
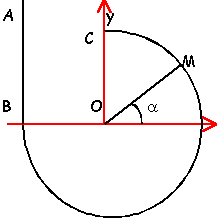
Le mobile de masse m
est laché de A sans vitesse. Il se
déplace dans une glissière ABMC, sans
frottements. Au dela de C, il n'est soumis
qu'à son poids
AB=h=1 m ; OB=r=50 cm;
g=10 ms-2.
- Quelle est la vitesse du mobile en C en
ms-1 et km h-1.
- Donner l'équation de la trajectoire
du mobile au dela de C
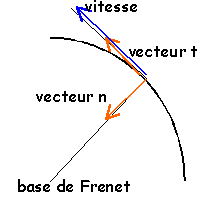
- Exprimer l'accélération du
mobile en M en fonction de h, g, r et
a.
|
|
|
|
|
corrigé
|
|
|
|
|
th de l'énergie cinétique
entre A et C (l'origine des
altitudes est celle du point O
) ou bien on
écrit que l'énergie mécanique
se conserve.
l'altitude de C doit
être inférieure à celle de A,
sinon C n'est pas atteint
(on part sans
vitesse de A)
Energie mécanique
en A = énergie potentielle = mgh
Energie mécanique
en C = 0,5 mV²C + mg R
V²C
=2g(h-r) = 2*10(1-0,5)= 10
VC=3,16
ms-1=3,16*3,6 km h-1
au dela de C,
chute libre, le solide n'est soumis qu'à son
poids.
expression de
la vitesse en M :
conservation de
l'énergie mécanique entre A et
M:
mgh = 0,5
mV²M + mg r sin(a)
V²M
=2g(h-r sin(a))
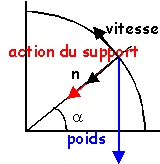
accélération
normale du mobile en M
aN
=V²M/rayon
=
2g(h/r-sin(a))
accélération
normale du mobile en M
écrire la seconde
loi de newton suivant un axe colinéaire
à la vitesse et de même sens
aT=
-gcos(a)
|
dans le repère
proposé
origine des temps: le
passage en C
accélération
(0; -10)
vitesse en
C (-3,16 ;
0)
position
OC (0; 0,5)
vitesse à
la date t
(
-3,16;
-10
t
)
position
à la date
t-3,x=-3,16t
y=-5t²+0,5
trajectoire
y= -5/3,16²
x²+0,5
|
|
|
|
exercice
4
|
relais
4 x 400
|
|
Un coureur X arrive avec un mouvement uniforme
v=7,5 ms-1. A 10 m devant lui, le
coureur Y s'élance d'un mouvement
uniformèment accéléré
a=2 ms-2.
- Quel temps s'écoule entre le moment
où Y démarre et le passage du
témoin.
- Pendant cette durée quelles sont les
distances parcourues par X et Y.
Tous les coureurs ont une
accélération de 2 ms-2
jusqu'à atteindre une vitesse v= 7,5
ms-1 qu'il conserve jusqu'au passage du
témoin. Les passages du témoin se
font tous les 400 m. Quelle est la durée de
la course ?
|
|
|
|
corrigé
|
|
|
|
|
origine des temps:
t=0 au démarrage de
Y
origine des abscisses:
position de Y à t=0
équations
horaires:
coureur
X:
x=7,5t-10
coureur
Y:
x=t²
tant que la vitesse est inférieure à
7,5 ms-2.
passage du témoin : les deux
coureurs se rejoignent
7,5t-10
=
t²
la résolution
donne
t=1,73 s
la seconde solution t=5,77
s :si X continue
à courir à la même vitesse , il
va rattraper Y
distance
parcurue par X en 1 ,73 s
à la vitesse de 7,5
ms-1, en 1,73 s X parcourt une distance
de :1,73*7,5=
13 m
le premier
coureur démarre avec une vitesse
nulle:
mouvement
uniformément accéléré
jusqu' à atteindre la vitesse de 7,5
ms-1 puis mouvement uniforme
x=t² donc v= 2t ;
t=7,5/2=
3,75 s durée du
mvt accéléré.
il a
parcouru:
x=3,75²=
14,06 m
il lui reste a parcourir
400-14,06 = 385,94 m à la vitesse de 7,5
ms-1.
La durée de ce
mvt est
385,94/7,5=51,46
s soit au total la
course du premier
dure:
55,2 s.
au passage du
témoin quelle est la vitesse du second
?
3 m parcourus:
3=0,5
*2*t² ;
t=1,732 s
;
v=2t=3,46
ms-1
il lui reste à
parcourir 400 m avant de rattraper le 3
ème.
mvt uniformèment
accéléré jusqu' à
atteindre la vitesse de 7,5 ms-1 puis
mouvement uniforme
on ne change pas les
origines définies ci dessus.
x=0,5*2*(t-55,2)²+3,46
(t-55,2) +400
v=2((t-55,2)+3,46
=7,5
d'où
t=55,2+2,02=57,2 s
durée de
l'accélération 2,02 s
la distance parcourue
est:
x-400=2,02²+3,46*2,02=11,06
m
il lui reste à
parcourir
400-11,06=388,94 m
à la
vitesse de 7,5
ms-1
durée =51,85
s
durée de la course
du second (et du 3
ème):51,85+2,02=53,87s
par contre le dernier
parcourt 385,94 m
à la vitesse
de 7,5 ms-1
durée
51,46s
total:
216,4s
|
|
|
|
exercice
5
|
rotation
d'un ressort
|
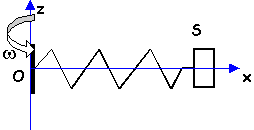
Le solide S de masse m=0,5 kg peut glisser
sans frottements le long de la tige Ox
(O
fixe). On fait tourner
l'ensemble autour de l'axe Oz à vitesse
angulaire w
=5 rad s-1 constante.
raideur k=100N
m-1. g=10 ms-2. longueur
à vide du ressort l0=1
m.
- Quel est l'allongement du ressort ?
- même question le ressort est
incliné d'un angle a
=30° sur l'horizontale.
- Dans ce dernier cas déterminer la
tension T du ressort.
|
|
|
|
|
corrigé
|
|
|
|
|
La somme des forces
appliquées au solide S est égale au
produit de sa masse par
l'accélération.
Projeter cette
relation sur un axe horizontal à
gauche.
k(L-L0)=mw²
L
(k- mw²)
L =
kL0
L=
100/(100-0,5*5²)=1,143
m
allongement
0,143 m
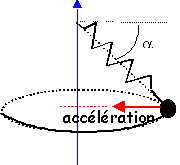
L'accélération est
centripète dirigée suivant l'axe n ;
le solide décrit un
cercle de
rayon
Lcos(a)
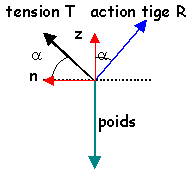
Même méthode
en projection sur T
T-mgsin(a)=mw²Lcos2a....T=k(L-L0)
L=( mgsin(a)+kL0)
/ (k-mw²cos2a)=1,131 m
d'où la tension
T=100(1,131-1)=13,1
N
|
|
|
|
|
exercice
6
|
vitesse
- accélération -
position
|
|
Soit la distribution de charges (microcoulombs)
ci contre ;AB=d= 0,2 m ;
Les deux charges
placées en A et B sont fixes; par contre la
charge placée en C est mobile sur la droite
AB.
Quelle est la position d'équilibre
de la charge placée en C, si elle existe
?On étudie le
mouvement d'un petit mobile sur un axe Ox. Son
accélération est constante de valeur
a=6 m s-2. Son abscisse initiale est
x=-2 m; sa vitesse initiale est -3
ms-1.
- A quelle date et à quelle abscisse,
le mobile s'arrète il puis change de sens
de parcours.
Un objet décrit une
trajectoire rectiligne; sa vitesse initiale est
nulle et les deux premières secondes, son
accélération valant 2 m
s-2. Les deux secondes suivantes son
accélération est nulle.
Quelle est la
distance parcourue durant ces 4 secondes
?
|
|
|
|
corrigé
|
|
|
|
|
La vitesse est une
primitive de l'accélération
v=at+v0
.....
v=6t-3
le mobile s'arrète
si la vitesse s'annule ;
t=0,5 s
puis il change de sens de
parcours (mvt uniformément
accéléré )
La position est une
primitive de la vitesse
x=0,5
at²+v0t+x0
.....
x=3t²-3t -2
abscisse à t=0,5 s
: 3*0,5²-3*0,5-2=
-2,75
origines de temps et des distances :le
départ
|
intervalle
|
position
|
vitesse
|
accélération
|
|
|
[0;2]
|
x=t²
|
v=2t
|
a=2
|
x(t=2)=4
m
|
v(t=2)=4
ms-1
|
|
[2;4]
|
x=4(t-2)
|
v=4 ms-1
|
a=0
|
x(t=4)=8
m
|
|
total : 12 m parcourus
|
|
|
exercice
7
|
|
Un solide de masse M=2kg, est
treuillé sur un plan incliné
d'un angle a
sur l'horizontal. frottements
négligé; départ sans
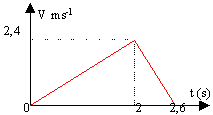
vitesse. Le cable casse à t=2 s .
Le graphe ci contre représente la
vitesse en fonction du temps lors de la
montée.
- Déterminer les
accélérations et
a.
- Quelle est la distance parcourue
lors de la montée ?
- déterminer la tension du
cable.
|
|
|
corrigé
|
|
|
les coefficients directeurs des
droites donnent les
accélérations(ms-2)
a1=
1,2 ;
a2
= -4 (cable
cassé et fin de la montée
)
a2=-gsin(a)
d'où
a
=
24°
axe
parallèle au plan vers le
haut
origines des
dates et des distances : bas du plan. Les
équations horaires sont
:
t < 2
:
d1=0,6 t²=
2,4
m
t > 2 :
d2=
-2(t-2)²+2,4(t-2) +
d1
d2=
-2*0,6²+2,4*0,6+2,4 =
3,12
m
|
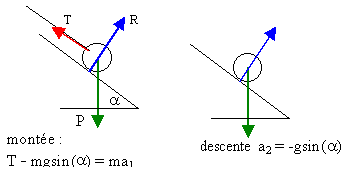
T=m(a1+gsin(a))
T=2(1,2+4)=
10,4
N.
|
|
|
|