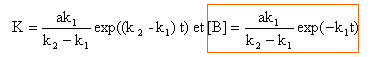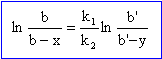réactions simples opposées

réactions simples successives

réactions simples parallèles jumelles

principe de Bodenstein

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

A--> B constante de vitesse k₁.

et B--> A constante de vitesse k₂.

à l'instant initial t=0 : [A]₀ =a ; [B]₀ =0

	A	B
initial	a	0
en cours	a-x	x

vitesse de la réaction totale :

v = d[B] /dt = k₁[A] -k₂[B]

dx/dt = k₁(a-x) -k₂x

dx/dt + (k₁+ k₂) x = k₁a (1).

solution générale de dx/dt + (k₁+ k₂) x =0

x = Cte exp (-((k₁+ k₂) t )

solution particulière de (1) : x = k₁a / (k₁+ k₂)

solution générale de (1) :

x = Cte exp (-((k₁+ k₂) t ) + k₁a / (k₁+ k₂)

0 = Cte + k₁a / (k₁+ k₂)

solution :

A--> B constante de vitesse k₁.

et B--> C constante de vitesse k₂.

à l'instant initial t=0 : [A]₀ =a ; [B]₀ =[C]₀ =0

vitesse de disparition de [A] :

v = -d[A] /dt = k₁[A]

[A] = Cte exp(-k₁t) avec à t = 0 : a = Cte

[A] = a exp(-k₁t).

v = d[B] /dt = k₁[A] - k₂[B] = k₁ a exp(-k₁t)- k₂[B]

d[B] /dt + k₂[B] =k₁ a exp(-k₁t) (1)

solution générale de d[B] /dt + k₂[B] =0

[B] = Cte exp(-k₂t) (2)

solution particulière de (1) :

méthode de la variation de la constante

dériver (2) : d[B]/dt = K' exp(-k₂t) -Kk₂exp(-k₂t)

repport dans (1)

K' exp(-k₂t) -Kk₂exp(-k₂t) + k₂K exp(-k₂t) = k₁ a exp(-k₁t)

K' exp(-k₂t) = k₁ a exp(-k₁t)

K' = k₁ a exp((-k₁+ k₂) t)

[B] = Cte exp(-k₂t) + ak₁ / ((-k₁+ k₂) exp(-k₁t)

.la constante d'intégration est déterminée d'après les conditions initiales:

0 = Cte + k₁a / (-k₁+ k₂)

solution :

A+ B --> C constante de vitesse k₁.

et A+ B --> D constante de vitesse k₂.

à l'instant initial t=0 : [A]₀ =a ; [B]₀ = b ; [C]₀ =[D]₀ =0

écrire les lois de vitesse :

v₁ = d[C] /dt = k₁[A][B]

v₂ = d[D] /dt = k₂[A][B]

d[C] /d[D] = k₁ / k₂

les concentrations de C et de D sont toujours dans un rapport constant dans le temps.

A+ B --> C constante de vitesse k₁, ordre 1 par rapport à B

et A+ B' --> D constante de vitesse k₂, ordre 1 par rapport à B'

l'ordre partiel par rapport à A est le même dans les deux réactions.

à l'instant initial t=0 : [A]₀ =a ; [B]₀ = b ; [B']₀ = b' ; [C]₀ =[D]₀ =0

à l'instant t : [C] =[x ; D] =y

Etablir une relation entre x et y

	A	B	B'	C	D
initial	a	b	b'	0	0
en cours	a-x-y	b-x	b'-y	x	y

écrire les lois de vitesse :

v₁ = d[C] /dt = k₁[A]^a[B]

v₂ = d[D] /dt = k₂[A]^a[B']

v₁ = dx/dt = k₁(a-x-y)^a(b-x)

v₂ = dy/dt = k₂(a-x-y)^a(b'-y)

rapport de ces deux dernières équations :

dx/dy = k₁(b-x) / ( k₂(b'-y))

dx /(b-x) = k₁ / k₂ dy / (b'-y)

intégrer :

-ln(b-x) = - k₁ / k₂ ln(b'-y) + Cte

les conditions initiales permetent de déterminer la constante.

-ln(b) = - k₁ / k₂ ln(b') + Cte

Cte = -ln(b) + k₁ / k₂ ln(b')

Les intermédiaires réactionnels restent en quantité pratiquement constante et très faible.

d[intermédiaire] / dt =0

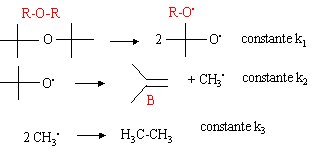
Déterminer la vitesse de la réaction dont le mécanisme est le suivant :

la réaction globale est : R-O-R --> 2 B + H₃C-CH₃.

v = ½ d[B] / dt

et d[B] / dt = k₂[R-O^.]

le principe de Bodenstein permet d'écrire : d[R-O^.] / dt =0

2k₁ [R-O-R] - k₂[R-O^.] =0

[R-O^.] = 2k₁ / k₂ [R-O-R]

v = ½ k₂ 2k₁ / k₂ [R-O-R] = k₁ [R-O-R].