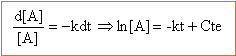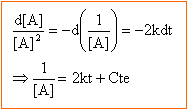Aurélie déc 2001


écrire la loi de vitesse et l'intégrer

exemple 1 ; exemple 2 ; exemple 3 ; exemple 4

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

 

réaction simple d'ordre 0 :
réaction simple d'ordre 1 :
réaction simple d'ordre 2 :
A--> B

d'une part : v = k [A]0= k

d'autre part : v = - d[A] / dt

d[A] = -k dt

par intégration : [A] = -kt + Cte

à t = 0 : [A]0 = Cte

[A] - [A]0 = -kt.
A--> B

d'une part : v = k [A]

d'autre part : v = - d[A] / dt

à t = 0 : [A]0 = Cte

ln ([A] /[A]0 )= -kt.
2A--> B

d'une part : v = k [A]2

d'autre part : v = - ½ d[A] / dt

1 /[A] - 1 /[A]0 = 2kt.
temps de demi réaction : à t = t½ , [A] = ½ [A]0
d'où : ½ [A]0 -[A]0 = -k t½.

t½ = [A]0 / (2k).
d'où : ln 2 = k t½.

t½ = ln 2 / k = Constante
d'où : 1 / [A]0 = 2k t½.

t½ = 1 / (2k[A]0).

Soit une réaction du type : A + B --> C. Trois expériences conduisent aux résultats suivants :
exp 1
exp 2
exp 3
103[A] mol /L
2
6,1
8,1
103[B] mol /L
2
2
6
103d[A] / dt mol /L/ s
0,032
0,29
1,5
En déduire les ordres partiels par rapport aux réactifs ?
La vitesse s'écrit : v = k [A]a [B]b

d'après les expériences 1 et 2 :

la concentration de A triple alors que celle de B reste constante.

dégénérescence de l'ordre : v = k1[A]a avec k1 = k[B]b

la vitesse est multipliée par 9 (0,29 = 9 * 0,032 ) alors que la concentration de A triple : a = 2.

d'après les expériences 1 et 3 :

la concentration de A quadruple en conséquence la vitesse sera multipliée par 16

la concentration de B triple alors que la vitesse est multipliée par 47 environ 16*3 : b = 1.

On considére la réaction : 2 NO2 -->O2 + 2 NO
t(min)
10
20
30
50
100
[NO2] mmol
0,91
0,84
0,78
0,68
0,52
Déterminer la constante de vitesse et l'ordre de la réaction.
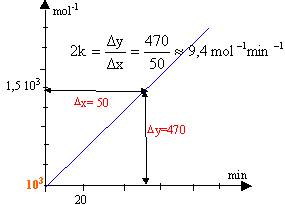
faire l'hypothèse : v = k [NO2]²

la loi de vitesse s'écrit : 1/[NO2] =1 /[NO2]0 + k t

tracer le graphe de la fonction 1/[NO2] = f (t)

d'où k = 9,4 / 2 = 4,7 mol-1 min -1= 4,7 /60 = 0,156 mol-1 s-1.

le graphe est une droite, l'hypothèse est bonne.

on déduit du graphe : 1 /[NO2]0 =1000 soit [NO2]0 = 10-3 mol.
On considére la réaction : 2 NO2 -->O2 + 2 NO
t½ (min)
35,6
21,4
10,6
0,53
[NO2]0 mmol
3
5
10
200
Déterminer la constante de vitesse et l'ordre de la réaction.faire l'hypothèse : v = k [NO2]²
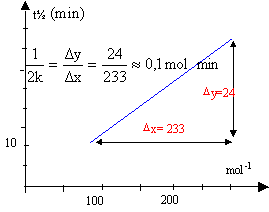
dans l'hypothèse d'un ordre deux : t½ = 1 / (2k[NO2]0)

tracer le graphe de la fonction t½ = f (1/[NO2]0)

d'où k = 5 mol-1 min -1.

le graphe étant une droite l'hypothèse est vérifiée.
On considère la réaction : (CH3)2CBr + H2O --> (CH3)3COH + H+ + Br-.
T(K)
280
286
290
298
104 k(s)
1,33
2,72
4,31
10,3
Déterminer l'énergie d'activation de la réaction.
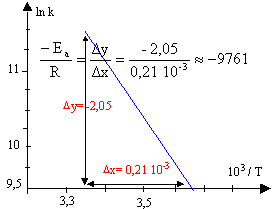
loi d'Arrhénius :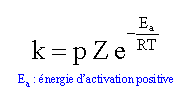

ln k = ln (pZ) -Ea / (RT)

tracer le graphe de la fonction : ln k = f(1/T)

Ea = 9761 *8,31 = 81,1 kJ/mol.

On introduit 10 -2 mole de soude et 10 -2 mole d' un ester soluble dans 1 litre d' eau à 27° C.

  1. Sachant que la réaction est d' ordre 2 et qu' au bout de 2 heures , les 3/4 de l' ester sont saponifiés , calculer la constante de vitesse et le temps de demi- réaction.
  2. La vitesse de la réaction est multipliée par 4 lorsque la température passe de 27 à 127° C. Calculer le temps de demi- réaction à 127° c ainsi que l' énergie d' activation de la réaction.
R-COOR1 + HO- = R-COO- + R1-OH
R-COOR1
HO-
R-COO-
R1-OH
initial
0,01 mol
0,01 mol
0
0
en cours
0,01-x
0,01-x
x
x
vitesse = k [ester][HO-]

dx/ dt = k(0,01-x)² soit dx / (0,01-x)² = kdt

par intégration kt = 1/(0,01-x) + Cte

à t=0, x=0 d'où Cte = -1/0,01

kt = 1/(0,01-x) -1/0,01

au bout de 2 heures : t= 2 ; 0,01-x = 0,01*0,25 =2,5 10 -3 mol

k= ½(400-100 ) = 150 mol L-1heure -1.

à t½ la moitié de l'ester a réagi soit x = 0,005 mol

t½ = 1 / (ka) avec a = 0,01 mol

t½ =0,66 heure = 40 minutes.

k= A exp ( -E/ (RT)

ou ln k = ln A -E/(RT)

ln k1= ln A-E/(300R)

ln k2 =ln (4k1)= ln A - E/(400R)

ln 4 + ln k1 = lnA-E/(400 R)

ln 4 +lnA-E/(300R) = lnA-E/(400 R)

ln 4= E/ R( 1/300 -1/400) = 10-4 E

E = 1,4 10 4 J .

à 127°C, la constante de vitesse quadruple donc t½ est divisé par 4 .

dans le cas où les quantités de matière initiales des réactifs sont différentes

a mol d'ester et b mol d'ion hydroxyde ( en excès)

dx/dt = k (a-x)(b-x)

dx / ((a-x)(b-x)) = kdt

1/(b-a)[dx/(a-x) - dx/(b-x)}=kdt

par intégration : 1/(b-a) ln[(b-x)/(a-x)]+Cte = kt

condition initiale : à t=0 , x=0 d'où la constante d'intégration Cte = - 1/(b-a) ln(a/b)

1/(b-a) ln[a(b-x)/((a-x)b)] = kt
Etude cinétique de la formation du complexe Cr III - EDTA par spectrophotométrie :

 

Toutes les études sont faites à un pH, à un volume et à une température que l’on peut considérer comme constants.

Dans un souci de simplification, on écrira l'équation de la réaction : Cr3+ + EDTA --> CrIII-EDTA

où EDTA désigne toutes les formes acido-basiques de l’EDTA non complexé et CrIII-EDTA désigne le complexe que l’on notera par la suite X.

La réaction est totale, elle est d’ordre partiel 1 par rapport aux ions Cr3+ et d’ordre partiel 1 par rapport à l’EDTA.

On suit le déroulement de la réaction par la mesure de l'absorbance A d’un échantillon de la solution prélevé à différentes dates t, à la longueur d’onde l = 540 nm.

A cette longueur d’onde, seuls Cr3+ et le complexe X absorbent. On notera e1 le coefficient d’absorbance molaire de Cr3+ et e1 le coefficient d’absorbance molaire de X.

On mélange 76,0 mL de solution d’EDTA à 0,100 mol.L-1 amenée préalablement à pH = 5,1 avec 4,0 mL d’une solution d’ions Cr3+ à 0,060 mol.L-1.

Les résultats sont :
t(min)
0
15
20
25
30
35
40
infini
A
0,033
0,1
0,12
0,14
0,16
0,,175
0,19
0,62

  1. Donner l’expression de la vitesse de la réaction en fonction d'une constante k et des concentrations molaires : [EDTA] et [Cr3+].
  2. Calculer les concentrations molaires initiales [EDTA]0 et [Cr3+]0 ; les comparer et en déduire une approximation qui simplifie la loi de vitesse.
  3. En déduire la loi cinétique intégrée, c’est à dire une relation entre [Cr3+]0, [Cr3+], kobs et t, en posant kobs = k[EDTA]0
  4. Exprimer A0, At et Ainf (respectivement absorbance à t = 0, absorbance à la date t et absorbance au bout d’un temps infini) en utilisant la loi de Beer-Lambert : on notera L la longueur de la cuve utilisée pour les mesures d’absorbance.
  5. Exprimer Ainf - A0, puis Ainf - At et montrer que ln (Ainf - A0)/(Ainf - At) = kobs.t
  6. Vérifier que les résultats expérimentaux confirment l’ordre 1 par rapport à Cr3+. Déterminer la valeur de kobs.
corrigé
v=k[Cr3+][EDTA]

concentration (mol/L) = Qté de matière (mol)/ volume de la solution (L)

Qté de matière (mol) = concentration (mol/L) * volume (L)

[Cr3+]0= C0=0,06*4/80=0,003 mol/L

[EDTA]0=0,1*76/80=0,095 mol/L en grand excès, donc a peu près constante

donc v = kobs [Cr3+] ;


Cr3+
+ EDTA
= X
initial
0,06*4 10-3 = 2,4 10-4 mol
0,1*0,076 = 7,6 10-3 mol
0
en cours d'évolution
2,4 10-4 -x mol

[Cr3+]t = (2,4 10-4 -x)/0,08

=[Cr3+]0- 12,5 x

=[Cr3+]0-[X]
7,6 10-3 -x
x

[X]=x/0,08 = 12,5 x
fin
2,4 10-4 -xfin=0

soit xfin=2,4 10-4 mol
7,6 10-3 -2,4 10-4

=7,36 10-3 mol
xfin=2,4 10-4 mol



[X]fin =2,4 10-4/0,08

= 0,03mol/L = [Cr3+]0
dx/dt = - kobs [Cr3+]= - kobs([Cr3+]0- 12,5 x)

dx / ([Cr3+]0- 12,5 x) = - kobs dt

par intégration : ln ([Cr3+]/Co)= -kobs t

ln ([Cr3+]0- 12,5 x) = -kobs t + Cte.

à t=0 , x= 0 d'où la constante : Cte = ln ([Cr3+]0)

ln ([Cr3+]0- 12,5 x) = -kobs t + ln ([Cr3+]0)

ln ([Cr3+]0- 12,5 x) - ln ([Cr3+]0) = -kobs t

ln (([Cr3+]0- 12,5 x)/[Cr3+]0) = -kobs t

ln (([Cr3+]/[Cr3+]0) = -kobs t .

loi de Beer-Lambert : A0=e1 L [Cr3+]0

Ainf = e2 [X]inf L avec [X]inf = [Cr3+]0 soit Ainf = e2 L [Cr3+]0

Ainf-A0= [Cr3+]0 L(e2-e1)

At= e1 [Cr3+]L+e2[X]L

Ainf -At =e2 L [Cr3+]0 - e1 [Cr3+]L+e2[X]L = e2 L([Cr3+]0- [X])-e1 [Cr3+]L

Or[Cr3+]0- [X]=[Cr3+]t

Ainf -At =e2 L[Cr3+]t-e1 [Cr3+]tL = [Cr3+]t(e2-e1)L

(Ainf - A0)/(Ainf - At) =[Cr3+]0 L(e2-e1) / ( [Cr3+]t(e2-e1)L )=[Cr3+]0/ [Cr3+]t

ln((Ainf - A0)/(Ainf - At))= ln ([Cr3+]0/ [Cr3+]t)= kobs t

(Ainf - A0) = 0,587.

t(min)
0
15
20
25
30
35
40
infini
A
0,033
0,1
0,12
0,14
0,16
0,175
0,19
0,62
(Ainf - At)
0,587
0,52
0,5
0,48
0,46
0,445
0,43
0
(Ainf - A0)/(Ainf - At)
1
1,129
1,174
1,23
1,28
1,32
1,365


ln((Ainf - A0)/(Ainf - At))
0
0,121
0,16
0,201
0,243
0,277
0,311


kobs min-1.


8,07 10-3
8 10-3
8,04 10-3
8,12 10-3
7,91 10-3
7,78 10-3


valeur moyenne de kobs=8 10-3min-1.

écart relatif = (8,12-7,78)/8 = 0,04 ( 4%)

kobs est constant à 4 % près et en conséquence les résultats expérimentaux confirment l’ordre 1 par rapport à Cr3+.



retour - menu