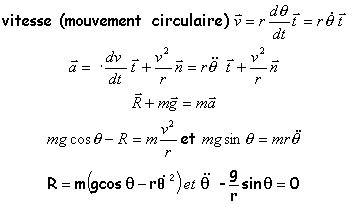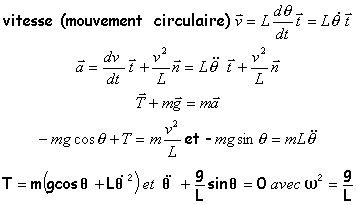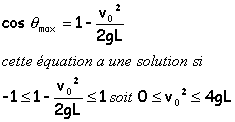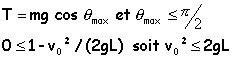|
|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
1 réaction du support |
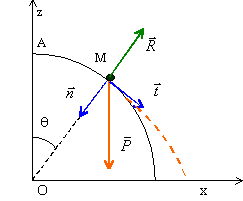
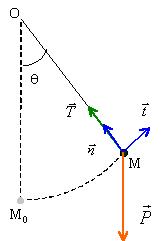
Les frottements sont négligés. Exprimer dans le repère de Frenet l'accélération de la bille. Ecrire l'équation différentielle du mouvement en fonction de q et de ses dérivées. Exprimer la réaction du support. corrigé |
|
|
|
projection de la relation fondamentale de la dynamique du point dans le repère de Frenet.
|
|
|
vitesse de la bille |
Exprimer les énergies potentielle, cinétique et mécanique en fonction de q et q'. En déduire la vitesse de la bille à chaque instant
corrigé |
|
|
|
Energie cinétique : 0,5 mv²= 0,5 mr²q'² Energie potentielle de pesanteur (origine en O) : mgz = mg r cos q. Energie mécanique : E= 0,5 mr²q'² + mg r cos q. En absence de frottements, l'énergie mécanique se conserve. Sa valeur initiale est E = mgr mgr = 0,5 mr²q'² + mg r cos q. gr = 0,5 r²q'² + g r cos q r²q'²=
v²
= 2gr(1-cos
q)
|
|
|
la bille quitte le support |
Exprimer la réaction du support en fonction de m, g, q. Pour quelle valeur de q, la bille quitte -t-elle le support ? Quelle est alors sa vitesse ? corrigé |
|
|
|
R= mg ( 3 cosq -2). La bille reste en contact tant que la réaction du support est positive ou nulle. 3 cosq -2 > 0 ou cos q >2/3 soit q<48° La vitesse de la bille vaut alors : v² = 2gr(1-cos q) = 2gr(1-2/3) = 2gr / 3 |
|
|
pendule simple équation horaire période |
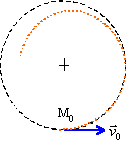
La bille est lancée de la position d'équilibre stable M0 avec une vitesse v0 horizontale. Ecrire l'équation différentielle du mouvement (cas des amplitudes faibles). Donner l'équation horaire et exprimer la période en fonction de L et g ( L = longueur du pendule)
corrigé |
|
|
|
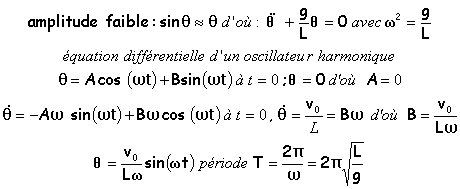
|
|
|
aspect énergétique |
Montrer que par dérivation par rapport au temps on retrouve l'équation différentielle du mouvement. corrigé |
|
|
|
Energie potentielle de pesanteur (origine en M0et axe vertical ascendant) : mgz = mg L(1- cos q). Energie mécanique : E= 0,5 mL²q'² + mg L(1- cos q). En absence de frottements, l'énergie mécanique se conserve. Sa valeur initiale est E = 0,5mv0² 0,5mv0² = 0,5 mL²q'² + mg L(1- cos q). 0,5v0² = 0,5 L²q'² + g L(1- cos q). L²q'²= v² = v0² - 2gL(1-cos q) En dérivant cette expression par rapport au temps : L² 2q' q" = 2gL q' (-sinq) Lq" + gsinq =0 |
|
|
différents types de mouvement |
corrigé |
|
|
|
v² = v0² - 2gL(1-cos qmax) = 0
Le fil doit d'autre part rester tendu : T positive ou nulle T= mg cos qmax + mLq'²
Si v0² est supérieur à 4gL il n'y a pas de mouvement oscillatoire autour de M0. Le fil doit d'autre part rester tendu lorsque q = p. v²(q = p) = v0²-4gL T(q = p) = mg cos p + mv²(q = p) / L positive ou nulle -mg + m(v0²-4gL)> 0 si v0²> 5gL mouvement circulaire si 2gL > v0² > 5gL
|