En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||
|
||||||||
|
On laisse tomber un objet de masse m = 1 kg du haut d'une tour de hauteur h = 50 m avec une vitesse initiale v0 = 600 m/min. g = 10 m s-2 ; 1100½ =33 ; 1000½=32. La vitesse de cet objet arrivé au sol est de 60 m/s. Faux. L'énergie mécanique initiale est sous forme d'énergie cinétique et d'énergie potentielle de pesanteur. L'origine de cette énergie est choisie au sol. EM= mgh + ½mv02. L'énergie mécanique juste avant l'arrivée au sol est sous forme cinétique : EM= ½mv2. L'énergie mécanique se conserve : ½mv2 = mgh + ½mv02 avec v0 = 600/60 = 10 m/s v2 = 2gh + v02 ; v = [2gh + v02 ]½ =[20*50+ 102 ]½ =1100½ =33m/s. L'énergie cinétique est 512 J. Faux. ½mv2 = 0,5*1100 = 550 J. On ne néglige plus les frottements de l'air que l'on assimile à une force de frottements constante de 1 N. La vitesse de cet objet arrivé au sol est de 50 m/s. Faux. Travail résistant des frottements lors de la chute : - f h = -1*50 = -50 J Travail moteur du poids lors de la chute : mgh = 1*10*50 = 500 J. Somme des travaux : 450 J. La variation de l'énergie cinétique est égale à la somme des travaux des forces : ½mv2 - ½mv02 = 450 ; v2 = v02 +900 = 100+900 = 1000 ; v = 1000½ = 32 m/s. L'énergie cinétique est 400 J. Faux. ½mv2 = 0,5*1000 = 500 J.
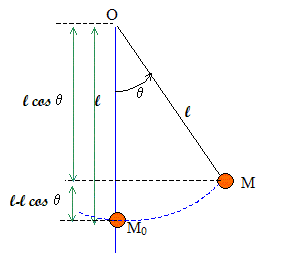
On considère un pendule simple
constitué d'une masse m ponctuelle
accrochée au bout d'une tige rigide de masse
négligeable et de longueur L. Cette barre
est articulée autour d'un point O fixe et
peut se mouvoir dans le plan vertical. On
repère la position du pendule par l'angle
q qu'il fait avec la
verticale. L'origine de l'énergie
potentielle est prise lorsque q
=0. Dans l'état initial le pendule est
lancé avec les conditions suivantes : q 0=0 ;
[dq/dt]0 =a(g/L)½
; a est constant et les
frottements sont négligeables.
Pistolet. Un pistolet tire un projectile en l'air de sorte su'il attaigne une hauteur de 20 m. Le même pistolet tire une seconde fois avec le ressort comprimé moitié moins que la première fois. On négligera les frottements. La hauteur atteinte lors du second tir est 10 m. Faux. L'énergie potentielle élastique du ressort ½kx2 est convertie en énergie cinétique ½mv2 puis en énergie potentielle de pesanteur mgh. L'énergie mécanique du système { ressort projectile } se conserve : ½kx2 = mgh Si x est divisé par deux, alors h est divisé par 4 : la hauteur atteinte est seulement de 5 m. L'énergie potentielle élastique du ressort est totalement convertie en énergie potentielle de pesanteur lors du tir. Faux. L'énergie potentielle élastique se retrouve sous forme potentielle de pesanteur et sous forme cinétique. Au point le plus haut l'énergie cinétique étant nulle, l'énergie potentielle élastique est sous forme potentielle de pesanteur. Un travail moteur effectué sur un objet dont on néglige l'énergie potentielle gravitationnelle, a une énergie cinétique qui ne varie pas. On peut conclure qu'il subit une force de frottement. Vrai. On peut conclure que cette situation est impossible. Faux. Soit un objet se déplaçant sur un plan horizontal : l'énergie potentielle de pesanteur est constante et peut être choisie comme nulle. Si l'énergie cinétique ne varie pas, la valeur de la vitesse est constante : le mouvement est rectiligne uniforme. Le travail moteur est donc compensé par un travail résistant.
On s'intéresse à l'énergie d'une masse m soumise à la force de rappel d'un ressort de constante de raideur k. Cet oscillateur s'amortit au cours du temps sous l'effet d'une force de frottement de valeu f= b v avec b coefficient de frottement dynamique et v la vitesse. On donne l'équation de mouvement de cet oscillateur amorti x" + b/m x' +k/m x=0. On pose w02 = k/m et Q= m/b w0. L'énergie s'écrit E = E0 exp(-b/m t) avec E0, énergie mécanique à t=0. On pourra faire l'approximation e-x~ 1-x ; ln3 ~1 ; ln(2/3)~0,4. La fraction de l'énergie perdue pendant une période du mouvement est DE/E = -2pb/(mw0). Vrai. On note la période T =2p/w0 ; E(T) = E0 exp(-bT/m) ; E(2T) = E0 exp(-2bT/m). DE/E = [ E(2T)- E(T) ]/E(T) = exp(-2bT/m) / exp(-bT/m) -1 = exp(-bT/m) -1 Si bT/m est petit : exp(-bT/m)~ 1-bT/m ; exp(-bT/m) -1 ~ -bT/m. [k/m]½ a la dimension d'une période. Faux. w0 = [k/m]½ ; w0 a la dimension d'une pulsation en rad/ seconde. On prend w0 = 10 ; Q=400. L'équation du mouvement de cet oscillateur est : x(t)=A exp(-bt/m) cos (w0t). ( A = constante) Vrai. On pose l= ½b/m ; x(t)=A exp(-lt) cos (w0t). x' = -A exp(-lt) [l cos (w0t) +w0sin (w0t)] x" =l A exp(-lt)[l cos (w0t) +w0sin (w0t)] -A exp(-lt) [-l w0 sin (w0t) +w02cos (w0t)] x" =A exp(-lt) [(l2 -w02)cos (w0t)+2lw0sin (w0t)] Repport dans l'équation différentielle : x" +2l x' +w02 x=0 [ (l2 -w02)cos (w0t) +2l2cos (w0t)-2lw0sin (w0t) + w02 cos (w0t)=0 2l2cos (w0t) =0 : b/m = w0 /Q = 10/400 = 1/40 ; l= ½b/m =1/80 et l2 = 1/802~0 donc égalité vérifiée quel que soit le temps. L'amplitude des oscillations est réduite de 2/3 au bout de 100 s. Faux. b/m = w0 /Q = 10/400 = 1/40 ; x(100) =A exp(-100/40) cos(1000)=0,082*0,56 A =0,046 A.
Une gouttelette de pluie de forme sphérique de rayon 5 mm tombe de la base d’un cumulonimbus situé à une altitude de 4,5 km. On prendra comme origine des temps l’instant où la goutte quitte la base du nuage, comme origine de l’espace l’endroit où la goutte quitte le nuage et l’on négligera les frottements rencontrés lors de cette chute. g~ 10 m/s2 ; p~ 3 ; rair = 1 kg m-3 ; reau = 1000 kg m-3. L’équation horaire du mouvement de la gouttelette est y(t) = -½gt2. Faux. L'axe étant orienté suivant la verticale descendante y(t) = +½gt2. Le calcul ainsi fait à l’aide de ce modèle prévoit que la goutte atteint le sol avec une vitesse de 100 m/s. Faux. durée de la chute : t=(2y/g)½ =(9000/10)½ = 30 s. v(t) = gt =10*30 = 300 m/s. Un meilleur modèle devrait tenir compte des forces de frottements exercées par l’air sur la goutte ainsi que de la poussée d’Archimède. La poussée d’Archimède qui s’exerce sur la goutte est environ : 5 10-7 N. Faux. Valeur de la poussée : F = rair V g avec V = 4/3pR3 ~4*(5 10-3)3~ 5 10-7 m3 ; F~ 1*5 10-7 *10 = 5 10-6 N. La masse de la goutte est m=5 mg. Faux. m =reau V ~5 10-7 *1000 ~5 10-4 g soit 0,5 mg. |
||||||||
|
|
||||||||
|
|