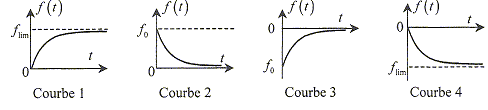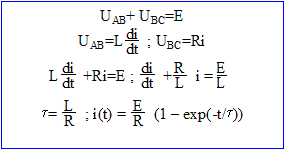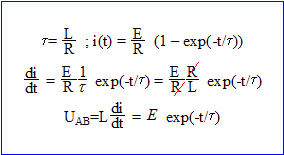Concours Esiee : 4 années de QCM dipôle RLC En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

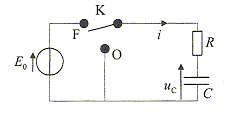
Le circuit RC est alimenté par un générateur de tension constante E0. Lors de la charge du condensateur : A- Le courant i à l'allure de la courbe 1. faux ; courbe 2 B- La tension uc à l'allure de la courbe 2. faux ; courbe 1 C- A la fin de charge le condensateur a emmagasiné l'énergie ½CE²0. vrai Lors de la décharge du condensateur ( position O de l'interrupteur) D- Le courant i à l'allure de la courbe 3. vrai discontinuité de l'intensité E- La tension uc à l'allure de la courbe 4. faux continuité de la tension uC.   Un circuit LC est parcouru par un courant i(t)= 0,005 sin ( 1000t) exprimé en ampère. L= 0,1 H. On note q(t) la charge du condensateur à l'instant t. A- La fréquence du courant est 1000 Hz. faux pulsation w =1000 = 2p f B- C= 10 mF. vrai période au carré T² = 4 p² ( LC) soit C = T² / (4 p² L) avec T= 2p/1000 ; C= 10-6 / L = 10-5 F C- |q(0)|=5 10-6 C.vrai i(t) = dq(t) /dt donc la charge est une primitve de l'intensité : q(t) =-0,005/1000 cos(1000t) ; q(0) = - 5 10-6 C ; |q(0)|= 5 10-6 C. D- u(t) = 0,5 cos (1000t) vrai u(t) = q(t) / C = 5 10-6 cos(1000t) /10-5 =0,5 cos(1000t) E- q(t) = 5 10-6[1-cos(1000t)] faux   Un dipôle RLC série est soumis à une tension sinusoïdale e(t) et parcouru par un courant i(t). C= 5 10-6 F. A- R= 250 W vrai ; R= 5/ 2 10-2= 250 ohms. B- L=20 mH vrai période T= 2 10-3 s (lecture fraphe) ; T²= 4 p² ( LC) soit L = T² / (4 p² C) = 4 10-6 /(40 *5 10-6) = 0,02 H C- Le circuit est à la résonance vrai i(t) et e(t) sont en phase. D- La puissance moyenne du circuit sur une période vaut 100 mW. faux intensité efficace =Ieff = 2 10-2 / 2½ ; tension efficace =Ueff = 5 / 2½ ; puissance consommée IeffUeff = 0,05 W = 50 mW E- La puissance dissipée par effet joule est nulle. 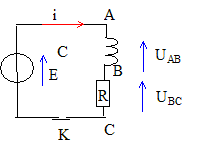faux RI²eff     Web www.chimix.com La bobine est supposée parfaite. A t=0 on ferme l'interrupteur K.   1. La constante de temps vaut-elle t = 1/(RL) ? faux 2. La constante de temps vaut-elle t = R/L ? faux 3. La tension aux bornes de la bobine vaut-elle UAB=E exp(-t/t)) ? vrai 4. L'intensité i(t) est-elle de la forme i(t) = I max(1-exp(-t/t)) ? exact 5. Au bout d'un temps très long, l'intensité du courant tend-elle vers E/R ? 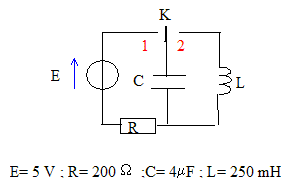exact En régime la bobine alimentée par une tension continue, se comporte comme un résistor ( ici r voisin zéro) A la date t=0 le condensateur est déchargé. De t=0 à t1 l'interrupteur est en position 1. Peu avant t1, on considère que le courant circulant dans le circuit RC n'évolue plus. A l'instant t2, l'interrupteur est en position 2. 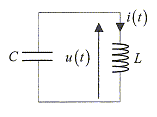1. L'énergie stockée dans le condensateur à t=t1 vaut-elle 0,05 mJ ? vrai Dés que le condensateur est chargé, l'intensité du courant dans le circuit RC reste nulle. La tension aux bornes du condensateur est E= 5 V. Energie stockée dans le condensateur : ½CE² =0,5 * 4 10-6 *25 = 5 10-5 J = 0,05 mJ. 2. L'énergie dissipée par effet joule vaut-elle 0,05 mJ ? vrai énergie fournie par le générateur entre les dates t=0 et t=t1 : EQ = , avec Q= CE charge finale de l'une des armatures du condensateur Or ½CE²= 0,05 mJ est stockée par le condensateur ; ½CE²= 0,05 mJ est dissipée dans la résistance. 3. A partir de t2, un courant périodique de période "2p" ms s'établit-il dans le circuit LC ? vrai période du dipole (LC) : 4. A partir de t1, l'énergie stockée dans la bobine L est-elle une fonction périodique de période "2p" ms ? faux énergie stockée dans la bobine : ½Li² i(t) est une fonction périodique de période "2 p" Le carré de l'intensité i²(t) est une fonction périodique de période "p". 5. A partir de t1, l'énergie totale du circuit LC est-elle constamment égale à 0,1 mJ ? faux L'énergie totale du circuit LC est égale à l'énergie initialement stockée par le soit 0,05 mJ. 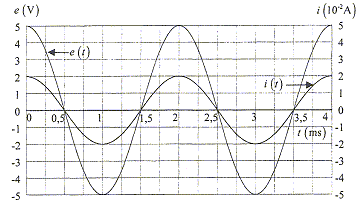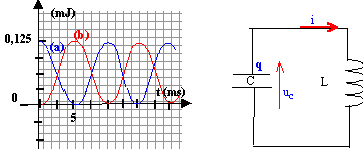Les courbes ci-dessous représentent les évolutions en fonction du temps de l'énergie du condensateur C, initialement chargé, et de l'énergie de la bobine supposée parfaite d'inductance L. Le courant i est sinusoïdal avec une amplitude de 50 mA. a) L'énergie totale du circuit vaut 0,25 mJ b) L= 0,1 H c) C= 1mF La fréquence du courant i est : d) 50 Hz e) 100 Hz L'énergie totale du circuit vaut 0,125 mJ a) faux. Quand la bobine stocke toute l'énergie : 0,125 10-3 = ½LI²m soit L= 0,25 10-3 /I²m= 0,25 10-3 /0,052 =0,1 H b)vrai. période des courbes ci-dessus : 10 ms = 0,01 s ; période de l'oscillateur LC= 0,02 s ; fréquence 1/0,02 = 50 Hz d) vrai ; e) faux. 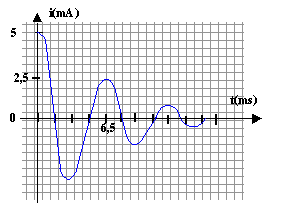T= 2p(LC)½ soit C= T²/(4p²L)= 0,02²/(4*3,14²*0,1) = 10-4 F c) faux. La courbe ci-dessous représente l'évolution du courant i(t) circulant dans un circuit RLC série pendant une durée de 20 ms. On donne C= 10 mF et p²=10. a) La pseudo-période T est légèrement supérieure à la période propre du circuit b) T est de l'ordre de 2p 10-3 s. c) L est de l'ordre de 0,1 H d) R<200 W e) R>200 W a) b) vrais T= 2p(LC)½ soit L= T²/(4p²C)= 10-6/10-5 = 0,1 H c) vrai. L'amortissement est d'autant plus grand que la résistance R est grande. d) faux ; e) vrai

retour -menu