Lentilles minces. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

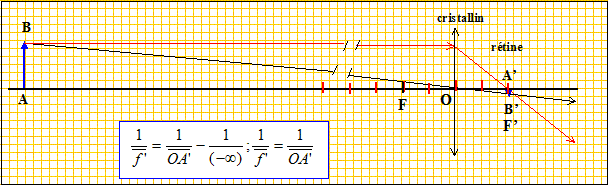
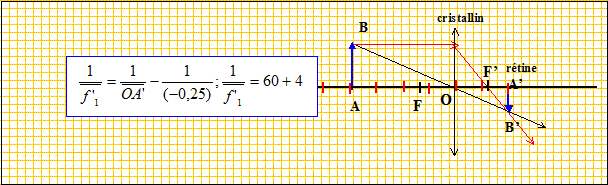
L'oeil. Texte : Le cristallin joue le rôle de lentille convergente. La rétine joue le rôle d'écran. Un oeil normal voit nettement un objet situé entre 25 cm et l'infini. Lors d'une observation sans fatigue ( objet à l'infini ), la vergence de l'oeil est C=60 d.  Les distances algébriques sont écrites en gras et en bleu. Analyse : Question relative à l'observation sans fatigue. Observation d'un objet à l'infini : 60 = 1/OA' ; OA' = 1/60 = 1,67 10-2 m = 1,67 cm. La distance cristallin -rétine est constante et vaut 1/60 = 1,67 10-2 m. Question relative à l'observation à 25 cm. La distance focale du cristallin diminue ; l'image nette se forme sur la rétine.   C1 = 64 d.   Projecteur diapositive. Texte : matériel : lentille convergente f'= 25 cm ; écran vertical situé à 5,0 m de la lentille; diapositive carrée de côté 3 cm. L'axe optique de la lentille est perpendiculaire à l'écran et au plan de la diapositive. Analyse : Question relative à la dimension de l'image sur l'écran. dimensions de la diapositive : carré de 3*19 = 57 cm de coté.       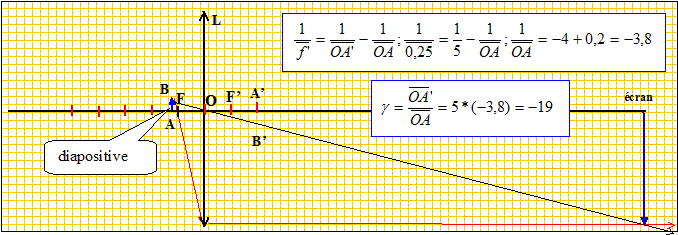Web www.chimix.com projecteur diapositive. Texte : l'objectif d'un projecteur de diapositives peut être assimilé à une lentille mince convergente. La diapositive étant disposée à 5 cm de l'objectif, on obtient une image nette lorsque l'écran est placé à 3,5 m de l'objectif. Analyse : Question relative à la distance focale f'. vergence C= C= 1/OA'- 1/OA = 1/3,5 - 1/(-0,05) = 20,286 distance focale = inverse de la vergence = 1/20,286 = 0,0492 m = 4,9 cm. Objet à l'infini. 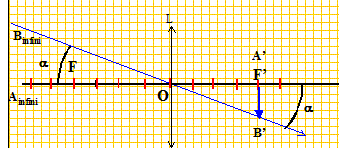Texte : la vergence d'une lentille est C=20 d. Un objet vertical AB,situé à l'infini est vu sous un angle a=3° depuis le point O, centre optique de la lentille. Analyse : Question relative à la hauteur de l'imageA'B'.   L'objet étant à l'infini, son image se trouve dans le plan focal image. exprimé 3 degrés en radians : a=3*3,14 / 180 = 5,23 10-2 rad. tan a = A'B' / OF' vosin de a radian pour les angles petits. hauteur de l'image (m) = a (radian)* distance focale(m) distance focale (m) = inverse de la vergence en dioptries = 1/20 = 0,05 m hauteur image = 5,23 10-2 *0,05 = 2,6 10-3 m = 2,6 mm. 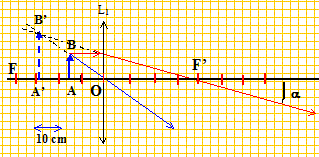Objet à l'infini. Texte : Objet : AB = 5 cm, perpendiculaire à l'axe optique d'une lentille convergente, situé 60 cm à gauche de la lentille. Image réelle, renversée, deux fois plus grande que l'objet. Analyse : Question relative au grandissement transversal g. L'image étant renversée, le grandissement est négatif. La taille de l'image étant deux fois celle de l'objet, le grandissement vaut : |g|=2 soit g = -2. Question relative à la distance focale image de la lentille. Les grandeurs algébriques sont écrites en gras et en bleu. g=-2 = OA'/OA d'où OA'=-2OA ; OA = -0,6 m ; OA'= 1,2m. Ecrire la formule de conjugaison : 1/f' = 1/OA'-1/OA. 1/f' = 1/1,2 -1/(-0,6) =2,50 ; f' = 1/2,5 ; f'= 0,40 m. On place l'objet 15 cm à gauche de la lentille. Question relative aux caractéristiques de l'image. La lentille fonctionne en loupe : l'image est virtuelle, droite, plus grande que l'objet. Ecrire la formule de conjugaison : 1/f' = 1/OA'-1/OA avec OA = -0,15 m. 1/OA'= 1/f'+1/OA = 2,5 +1/(-0,15) =-4,16 ; OA'= -0,24 m g= OA'/OA = -0,24 /(-0,15) = 1,6 ; A'B' = 1,6 AB =1,6*5 ; A'B' = 8 cm. On place un oeil au foyer image de la lentille. Question relative au diamètre apparent de l'image.  tan a = A'B' / (A'O+OF') = 8/(24+40)=0,125 ; a =7,1° = 0,124 rad.

retour -menu