. .
mécanique des fluides incompressibles sup .. ..
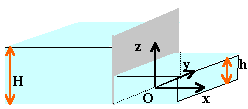
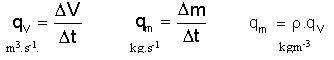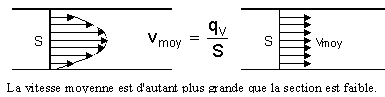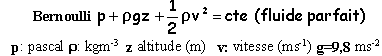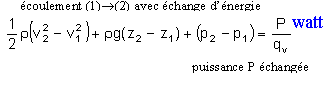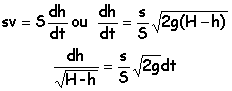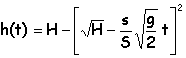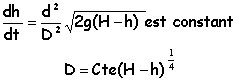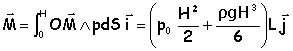révisions lycée (voir le Quiz)
cours 1	débit- vitesse- Bernoulli
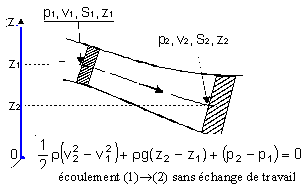
Parmi les fluides, on distingue les liquides (incompressibles) et les gaz (compressibles). 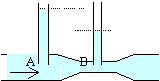débit volumique qV et débit massique qm : vitesse (ms-1)et débit (m3s-1) Le débit reste constant (liquide , gaz si température constante et vitesse faible) Bernoulli ( dans le cas de l'écoulement permanent d'un fluide parfait) P >0 si le fluide reçoit de l'énergie de la machine (pompe) P <0 si le fluide fournit de l'énergie à la machine (turbine)   applications Phénomène de Venturi Un conduit de section SA subit un étranglement en B où sa section est SB. La vitesse dufluide augmente dans l'étranglement, donc sa pression y diminue. Théorème de Torricelli réservoir muni d'un orifice de section s à sa base, s² <<S² (S section de la surface libre) la pression à la surface du liquide est égale à celle de sortie ( on néglige la variation de pression liée à l'atmosphère terrestre ) et le débit se conserve [sV2= SV1]. V2² = 2g z
cours 2	viscosité
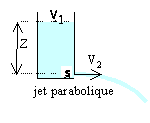
La viscosité h est due aux frottements ; ces derniers s'opposent au glissement des couches fluides les unes sur les autres. L'unité de viscosité dynamique est le Pascal seconde (Pa s) ou Poiseuille (Pl) . La viscosité des liquides diminue si la température augmente. pertes de charge Un fluide réel, en mouvement, subit des pertes d'énergie à cause des frottements sur les parois des canalisations. écoulements laminaire ou turbulent. 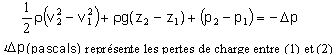Le nombre de Reynolds (sans unité) permet de déterminer si un écoulement est laminaire ou turbulent r : masse volumique du fluide (kgm-3) ; v : vitesse moyenne(ms-1), D : diamètre de la conduite (m) h = viscosité dynamique du fluide (Pa s) Re < 2000 écoulement laminaire Re > 3000 écoulement turbulent Bernoulli appliqué à un fluide réel avec pertes de charge débit si écoulement laminaire : loi de Poiseuille
cours 3	capillarité
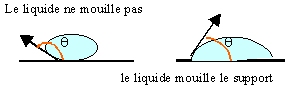
On retrouve cet angle à la surface libre d'un liquide près des bords du récipient ; il provoque la formation d'un ménisque dans les tubes. Les agents tensioactifs abaissent la valeur de la tension superficielle des liquides dans lesquels ils sont ajoutés pour les rendre mouillants, détergents, émulsifiants. Un tube capillaire est un tube de rayon intérieur faible. Plongé un tube capillaire, ouvert aux 2 extrémités, dans un liquide, provoque la montée du liquide mouillant ou la descente du liquide non mouillant d'une hauteur h.
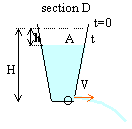exercice 1	vidange d'un réservoir, la clepsydre
Le récipient est à symétrie de révolution autour d'un axe vertical Quelle est la vitesse de l'eau sortant due l'orifice de section s? Quelle forme faut il donner au récipient pour que H-h soit une fonction affine du temps ? corrigé Th de Bernoulli entre la surface A et l'orifice de sortie O: le fluide est à la pression atmosphérique en A et en O. La vitesse en A est négligeable devant la vitesse V en O si S>>s rg(H-h)= 0,5 r V² d'où V²=2g(H-h) conservation du débit volumique entre un point de la surface et l'orifice dh/ dt étant la vitesse en A par intégration : forme du récipient
exercice 2	seringue
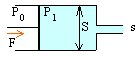
Le piston se déplace sans frottement ; le liquide est supposé parfait de masse volumique r. Exprimer le débit volumique a en fonction de la vitesse d'écoulement v dans l'aiguille et V dans le corps de la seringue Exprimer la force que l'opérateur doit exercer sur le piston en fonction du débit a et des données. corrigé conservation du débit volumique entre le corps de la seringue et l'aiguille vs=VS relation de Bernoulli entre ces mêmes points P1 + 0,5 rV² =P0 + 0,5 rv² P1 -P0 =0,5 r(V²-v²) Ecrire que le piston est à l'équilibre en régime permanent (pas d'accélération) F+P0 S-P1 S=0 F=(P1-P0)S
exercice 3 forces de pression sur la porte d'une écluse Une porte d'écluse de largeur L retient de l'eau liquide supposé incompressible de masse volumique r. Calculer à l'équilibre la résultante et le moment résultant (par rapport à O) des forces de pression s'exerçant sur cette porte. Montrer que ce torseur est équivalent à une force appliquée en un point C, appelé centre de pression que l'on déterminera. H=6 m ; h=2 m ; L=4 m ; corrigé forces de pression On note p0 la pression de l'air ambiant. pression dans le liquide à une altitude z à gauche : p = p0+ r g (H-z) à droite : p = p0+ r g (h-z) force pressante sur une surface de largeur L de hauteur dz située à l'altitude z liquide à gauche : p Ldz = (p0+ r g (H-z))Ldz dirigée à droite intégrer entre 0 et H liquide à droite : p Ldz = (p0+ r g (h-z))Ldz dirigée à gauche intégrer entre 0 et h force pressante due à l'air (partie droite) p0Ldz intégrer entre h et H résultante des forces de pression : F = 0,5 r g L (H²-h²) dirigée suivant Ox moment résultant par papport à O partie gauche partie droite On cherche à mettre ce moment sous la forme les vecteurs moment et force ayant les expressions ci dessus. applications numériques : F = 2,3 105 N et OC = 2,17 m retour - menu