Caractéristiques d'une bobine réelle d'après Mines 01. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .

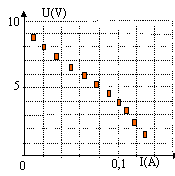
étude du générateur On se place en régime continu. En faisant débiter le générateur dans des résistances réglables, on obtient la figure ci-dessous : En précisant le domaine de validité en intensité, déduire de ces mesures un modèle linéaire du générateur: calculer la tension à vide, la résistance interne et le courant de court circuit. Ce générateur alimente un cicuit de résistance R ; calculer la valeur minimale de R assurant de ne pas sortir du domaine linéaire. corrigé si I <0,1 A la caractéristique du générateur est linéaire. 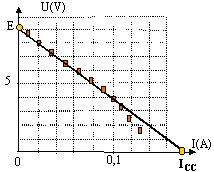L'ordonnée à l'origine donne la tension à vide E= 9 V ; l'intersection avec l'axe des abscisses donne le courant de court circuit ICC= 0,18 A. On en déduit la résistance interne r1 = E / ICC= 9 / 0,18 = 50 W. Le générateur fonctionne dans son domaine linéaire si l'intensité reste inférieure à 0,1 A. R doit être supérieure à Rmin: 0,1 ( Rmin+ r1) = 9 soit Rmin = 9/0,1 - r1 = 90-50 = 40 W.

étude rapide du bobinage Le grand nombre de spires du bobinage nécessite une grande longueur de fil, ce qui confère au dipole une résistance non négligeable. Un multimètre donne la valeur r = 7,9 W. Le fil de cuivre du bobinage présente une section de l'ordre de 1 mm2 et la conductivité du cuivre est s =6 107 Sm-1. En déduire une estimation de la longueur du fil. En réalité la longueur du fil est sensiblement inférieure à la valeur calculée : justifier. Les multimètres disponibles ne possédant pas de fonction inductancemètre, on détermine la valeur de l'inductance L en étudiant la résonance de courant dans un circuit RLC série. Le circuit RLC est alimenté par une tension sinusoïdale e(t)= E0cos(wt). - En utlisant les notations complexes, déterminer l'amplitude I0 de l'intensité du courant i(t) en fonction de E0, R, L, C,w. - A quelle pulsation le courant est-il en phase avec la tension d'alimentation ? La présence d'une résistanc r indissociable du dipôle d'inductance L modifie-t-elle cette propriètè ? Mise en pratique : On alimente le circuit série ( R, bobine r,L, condensateur C) à l'aide d'un GBF ; on visualise à l'oscilloscope la tension aux bornes du GBF et celle aux bornes de R On détermine expérimentalement la fréquence de résonance de l'intensité du courant et on en déduit par le calcul la valeur de L. - Faire le schéma du circuit et indiquer les branchements de l'oscilloscope. - Proposer une méthode permettant rapidement de déterminer la fréquence de résonance à l'aide de l'oscilloscope. - On repère la fréquence de résonance f = 774 Hz avec C= 470 nF ; déduire la valeur de L. corrigé résistance d'un conducteur cylindrique : R = L / (s s) : avec L: longueur (m) et s section (m²) L= Rs s = 7,9*6107*10-6= 474 m. si la longueur réelle est plus faible, alors le cuivre utilisé est impur : les impuretés diminuent la conductivité du matériau. impédance complexe du dipôle RLC série : Z = (R+r) + j(Lw-1/(Cw)) module de l'impédance : Z= [(R+r)² + (Lw-1/(Cw))²]½. module du courant : I0=E0 / Z = E0 / [(R+r)² + (Lw-1/(Cw))²]½. I0 est maximale à la résonance : I0 max = E0/(R+r) ; la pulsation propre vaut w 0 = (LC)-½. A la résonance d'intensité, la tension d'alimentation et l'intensité sont en phase ( l'impédance Z est réelle égale à la somme des résistances du circuit). Ce phénomène ne dépend pas de la résistance du circuit. 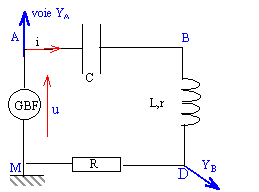Pour visualiser simultanément la tension d'alimentation délivrée par le GBF et l'intensité ( tension aux bornes de R au facteur R près) il faut que ces deux composants aient un point électrique commun relié à la masse de l'oscilloscope. On fait varier la fréquence du GBF et on repère la fréquence pour laquelle les deux courbes sont en phase. inductance de la bobine : L= [w 02 C ]-1 avec w 02 = 4p²f ² = 4*3,14²*774² = 2,36 107 . L=1 / [2,36 107 *470 10-9 ]=9 10-2 H = 90 mH.

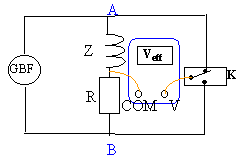
comportement électrocinétique de la bobine à basse frèquence On notera Z l'impédance complexe de la bobine et Z son module. On se propose de tester le modèle Z= r+jLw gràce au montage suivant : Le GBF est utilisé en mode sinusoïdal de fréquence f. Le bloc K est un interrupteur trois voies qui permet de mesurer soit la valeur efficace VA de la tension aux bornes de la bobine soit la valeur efficace VB de la tension aux bornes de R. Rappeler la définition de la valeur efficace de l'intensité d'un courant ou d'une tension variable ; Exprimer Z en fonction de R et des valeurs efficaces VA et VB. Quel est le rôle de R ? Supposons sue l'on dispose d'une série de valeurs[ f ; Z(f)]. Expliquer comment tester par une représentation graphiique la validité du modèle. On dispose des résultats de mesures :R= 500 W. f (Hz) 10 20 30 40 50 60 70 80 VA(mV) 99 146 203 253 317 365 432 492 VB(V) 5,4 5,3 5,3 5,3 5,4 5,4 5,4 5,4 - Déterminer r et L en expliquant la méthode utilisée; le modèle est-il bien validé ? - Les valeurs mesurées justifie-t-elle qu'on néglige souvent l'aspect résistif des dipôles inductifs de type bobine ? 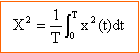corrigé Par définition, la valeur efficace X d'un signal alternatif x(t) de période T vaut : le multimètre posséde une impédance très supérieure à Z ou à R : Z= RVA/VB où R sert d'étalon ( de référence). Si le modèle est satisfaisant alors : Z² = r² +L²w²= r² +L²4p²f² calculer Z² à partir des mesures expérimentales puis tracer le graphe Z² en fonction de f ². 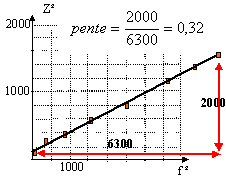f (Hz) 10 20 30 40 50 60 70 80 f ² 100 400 900 1600 2500 3600 4900 6400 Z² 84 182,7 356 568 894 1142 1600 2075 On obtient une droite de pente 0,32 ; 0,32 = L²4p² d'où L= 0,089 H.( en accord avec le calcul) r² = Z² - L²4p²f² = 2075-0,32*6400 = 32 soit r proche de 6 ohms. A basse fréquence le caractère résistif de la bobine est bien plus important que l'aspect inductif ; à 50 Hz : w = 2*3,14*50 = 314 rad/s; Lw= 0,089*314= 28, soit 4 fois supérieur à la résistance L'inductance L d'une bobine croît avec le carré de la longueur du fil tandis que la résistance augmente avec la longueur : l'aspect inductif l'emportera rapidement devant l'aspect résistif. retour - menu