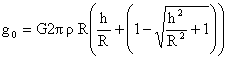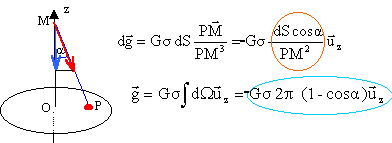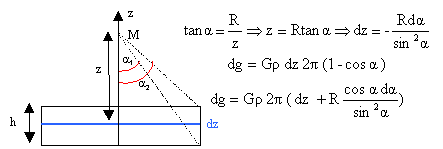Aurélie oct 2001
Une planète bien particulière

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

  1. On considère un disque de rayon R d'épaisseur négligeable, de masse surfacique s. Calculer le champ de gravitation r en un point M d'abscisse z0 de l'axe Oz du disque d'où l'on voit le disque sous l'angle a0.
  2. Le disque a maintenant une épaisseur h; on note r sa masse volumique. Montrer que le champ de gravitation g0 au voisinage de O, sur l'axe Oz est égal à :

    - si h / R = 10-3 calculer g0 à 1% près.
    - une planète de masse M= 6 1024 kg, est supposée avoir la forme d'un disque de rayon R, d'épaisseur h telle que h/R= 10-3, de masse volumique r= 5500 kg/m3. Le point O est au centre de la face nord. Calculer h, R et g0. Comparer g0 à la valeur 9,8 m/s2.
    - Comment évolue le champ de gravitation quant on s'éloigne de O , en se dirigeant vers le bord du disque. En déduire la position de repos des habitants de cette planète.

  3. On suppose que cette planète tourne autour de l'axe Oz avec une vitesse angulaire w, de période T=24h.
    - Comparer le champ de gravitation et l'accélération d'entraînement dans la zone équatoriale (bord du disque)
    - Dans quelle zone la position de repos vertical est-elle possible?
  4. tir au but : Dans le repère ci dessous, le gardien G a pour coordonnées (0; a); le ballon est au point B (0 ;-a). Le tireur communique au ballon une vitesse initiale v0 = 20m/s, dirigée vers O. On néglige les frottements de l'air et sur le sol. 2a=11 m.

    - Montrer que le mouvement du ballon est décrit par les équations : x" =w²+2wy' et y"=w²-2wx'
    - Déterminer les équations paramètriques du mouvement en posant w= x+ i y.
    - Simplifier les équations sachant que le temps de vol T du ballon jusqu'au but est tel que wT <<1.
    - Calculer le temps de transit T et l'abscisse X du point où la trajectoire du ballon coupe la ligne de but. Conclure.

corrigé
Le champ de gravitation est porté par l'axe Oz.

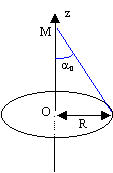
Tous les plans contenant un diamètre du disque et l'axe Oz sont des plans de symétrie pour la distribution de masse. Ils contiennent donc le vecteur champ de gravitation qui est par conséquent colinéaire à leur intersection c'est à dire Oz.

La contribution au champ crée en M par un petit élément de surface dS, de masse sdm, situé en P est :

Au voisinage de O, a =90° et g voisin de g0 = Gs2p , avec G constante de gravitation.

Ce calcul est identique au calcul du champ crée par un disque uniformément chargé en surface, en remplaçant 1 / 4pe0 par G

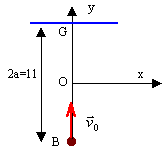
La contribution de l'épaisseur dz de masse rdS dz au champ crée en M est :

intégrer dz entre 0 et h

intégrer cosada / sin²a = - d (1/sina) entre a1 et a2

g = Gr 2p h - Gr 2p R ( 1/ sina2 - 1/ sina1 ).

avec sin a1 = R (R²+ z0²)-½ et sin a2 =R (R²+ (h+z0)²)-½

au voisinage de O, z0 =0 et g0 = Gr 2p h - Gr 2p R (1+ h²/R²)½ -1).

mettre Gr 2p R en facteur commun :

g0 = Gr 2p R[ h/R+1-(1+ h²/R²)½]

on peut négliger le terme h²/ R² du second ordre devant 1 si h/R vaut 10-3.

g0 voisin de Gr 2p h.

la masse de la planète est celle d'un cylindre de rayon R et de hauteur h

M= p R²rh avec R = 103 h, d'où M = p 106rh3

M= 106 *3.14*5500 h3 = 6 1024 kg

d'où h3 = 0,347 1015 et h = 70 km et R = 70000 km.

alors g0 = 6,67 10-11 *5500 *2*3,14*70 000 = 0,16 m/s².

valeur très inférieure à 9,8 m/s².

Quand on s'éloigne du centre O, le champ acquiert une composante radiale; il devient radial sur les bords du disque.

 

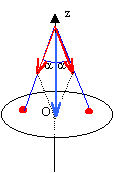
rotation de la planète :

Le champ de gravitation diminue lorsque l'on s'approche du bord du disque .

L'accélération d'entraînement est égale à w²R.

T= 24 *3600 = 86400 s; fréquence : 1/86400 = 1,157 10-5 Hz

w =2pf = 6,28 * 1,157 10-5 = 7,26 10-5 rad/s.

R= 70 000 km = 7 107 m

w²R = (7,26 10-5 )² * 7 107 = 0,37 m/s².

cette valeur est 2 fois plus grande que g0; les habitants sont satellisés.

La direction de repos est celle de la pesanteur, somme vectorielle de la force de gravitation et de la dorce d'entrainement.

La force de gravitation possède une composante axiale et une composante radiale centripète; la force d'entrainement est radiale centrifuge.

lorsque la force centrifuge compense la composante radiale de la force de gravitation, un habitant occupe une position de repos immobile.

tir au but :

Au voisinage de O le champ de gravitation est axial et uniforme. La force de gravitation et l'action du sol se neutralisent.

Il reste la force d'entrainement de composantes (mw²x ; mw²y)

et la force de Coriolis :

de composantes : 2mwy' et -2mwx'.

en projection sur le plan (O,x,y) le principe fondamental s'écrit :

x" = w² x +2wy' et y" =w²y-2wx'.

poser w = x + iy ; w'=x'+iy' et w"=x"+iy"

faire la somme x"+iy" en partant des deux équations ci dessus :

x"+iy" = w²(x+iy) +2w(y'-ix')

y'-ix' = -i²(y'-ix' )= -i(iy' = x') = -iw

w" = w² w -2 i ww'

w" +2 i ww' - w² w =0.

équation caractéristique associée : r² + 2 i w r -w² =0

r = - i w

solution de l'équation différentielle du second ordre

w= (A+ B t) exp (- i wt )

Les constantes A et B sont déterminées par les conditions initiales.

-ia = A (position initiale du ballon)

w' = [- i w(A+ B t) +B]exp (- i wt )

i v0 = - i wA+ B = wa +B ( vitesse initiale du ballon) --> B= i v0 -wa

A+Bt = -i a + i v0t -wat

w = (-i a + i v0t -wat) exp (- i wt ) = (-i a + i v0t -wat) [cos(wt ) -isin(wt ) ]

x = -wat cos(wt )+(a-v0t) sin(wt )

y =(-a+v0t) cos(wt )+ wat sin(wt )

si wt <<1 alors cos(wt ) voisin de 1 et sin(wt ) voisin de wt

x voisin de : -wat + (a-v0t)wt = -v0wt².

y voisin de : -a+v0t + w²at².

le temps de vol est T= 2a/v0 = 11 / 20 = 0,55 s

l'abscisse du ballon au niveau du but est : X = -20*7,26 10-5 *0,55² = -4 10-4 m

X est négligeable et le gardien ne doit pas bouger .

retour - menu