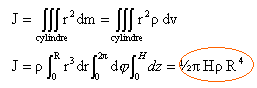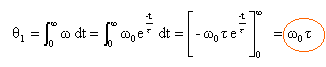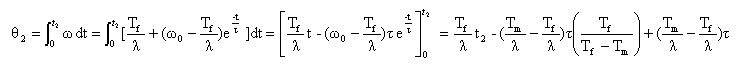Aurélie oct 2001
solide en rotation autour d'un axe fixe

 Capes physique appliquée 92

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

On considère un solide ayant la forme d'un cylindre droit, homogène ( de masse volumique r constante), de rayon R, de hauteur H, de masse m. Il est supposé constituer le rotor d'une machine tournante. On appelle J son moment d'inertie par rapport à son axe de symétrie D. Ce solide est mobile autour de son axe de symétrie D qui coïncide avec l'axe vertical fixe Oz d'un référentiel supposé galiléen.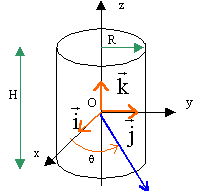

S'il est soumis à un couple de moment , celui ci sera supposé moteur lorsque T est positif, résistant dans le cas contraire. La rotation de ce cylindre par rapport à une position d'origine est repérée par l'angle q (t) . Elle est positive pour une rotation effectuée dans le sens direct. La vitesse de rotation du solide est donc donnée par la relation w (t) = dq(t) / dt = q'

  1. Etablir l'expression du moment d'inertie J de ce solide par rapport à son axe de symétrie D en fonction de m et R. Application numérique : R= 5 cm, H= 15,5 cm, J= 0,012 kgm². En déduire la masse volumique du matériau utilisé.
  2. Ce solide est soumis à un couple moteur constant de moment Tm et à un couple résistant, de type frottement fluide, ayant un moment de la forme Tr = -lw.
    - Etablir l'équation différentielle dont w (t) est solution.
    - Intégrer cette équation sachant qu'à l'intant t=0, la vitesse du rotor est nulle. On introduira la constante de temps t caractéristique de ce système et la vitesse angulaire limite w0 ( le nombre de tours/ minute correspondant est noté n0) théoriquement obtenue au bout d'un temps infini.
    - Tracer la courbe représentative des variation de w(t).
    - Vérifier que la tangente à l'origine coupe l'asymptote au point d'abscisse t = t.
    - application numérique : Tm = 3 N m ; n0= 1500 tr/min ; en déduire la valeur de la grandeur l, de la constante de temps t et de la puissance mécanique Pm exercée par le couple moteur en régime permanent.
  3. On suppose maintenant que ce rotor soumis au couple moteur constant de moment Tm et au couple de frottement fluide de moment Tr, tourne depuis très longtemps à la vitesse angulaire limite w0. A l'insatnt t=0 on annule brusquement le couple moteur précédent. Le solide n'est alors soumis qu'au couple résistant. Donner la nouvelle expression de w(t) . En déduire l'expression du nombre total N1 de tours effectués avant arrêt. Calculer N1.
  4. On suppose à nouveau que ce rotor soumis au couple moteur constant de moment Tm et au couple résistant de moment Tr tourne depuis très longtemps à vitesse angulaire constante w0. A l'instant t = 0 on annule brusquement le couple moteur et on applique un frein qui exerce un couple de moment Tf que l'on supposera constant ( et négatif).
    - Donner la nouvelle expression de w (t) .
    - En déduire le temps t2 que dure le mouvement ainsi que le nombre de tours N2 effectués avant arrêt.
    - application numérique Tf = -1 N m; calculer t2 et N2.
corrigé
Expression du moment d'inertie par rapport à un axe :

en coordonnées cylindriques, le volume élémentaire est dv = rdrdjdz

Exprimons la masse volumique en fonction de la masse et des dimensions du cylindre :

volume : pR²H ; masse m ; masse volumique r = m / ( pR²H)

repport dans l'expression de J : J= ½ pH m R4 / ( pR²H) = ½ mR².

application numérique :

m = 2J / R² = 2*0,012 / 0,05² = 9,6 kg

volume : 3,14 * 0,05² *0,155 = 1,216 10-3 m3.

masse volumique : 9,6 / 1,216 10-3 = 7889 kg /m3

c'est la masse volumique du fer.

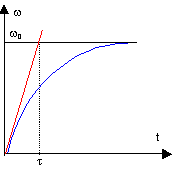
Le théorème du moment cinétique appliqué à un solide en rotation autour d'un axe fixe s'écrit :

J dw /dt = Tm-lw soit Jw' + lw = Tm.(1)

solution générale de l'équation différentielle sans second membre :

w =A exp ( - lt / J)

solution particulière de (1) : la vitesse limite est w 0 = Tm/ l.

solution générale de (1) : c =A exp ( - lt / J) + Tm/ l.

déterminer la constante sachant qu'à t=0 la vitesse angulaire est nulle

0 = A+Tm/ l d'où A = -Tm/ l

par suite : w (t)=Tm/ l[ 1- exp ( - lt / J) ] ; constante de temps t = J/ l .

la tangente à l'origine a pour coefficient directeur : (dw/dt) t=0 = w0 /t.

cette tangente coupe l'asymptote w =w0 à l'abscisse t = t.

application numérique :

w0 = 1500 /60 *2p = 157 rad/s.

l = 3 / 157 = 0,019 N m rad-1.

t = 0,012 / 0,019 = 0,631 s.

puissance mécanique ( en régime permanent ) du couple moteur : Pm = Tm w0 =  3*157 = 471 W.

courbe représentative des variations de w :

Le théorème du moment cinétique appliqué à un solide en rotation autour d'un axe fixe s'écrit :

J dw /dt = -lw soit Jw' + lw = 0

solution générale de l'équation différentielle :

w =A exp ( - lt / J)

déterminer la constante sachant qu'à t = 0, la vitesse angulaire est w0 =Tm/ l

A= Tm/ l. d'où w (t)=Tm/ l exp ( - lt / J)

avant arrêt le moteur effectue une rotation d'angle q 1 tel que:

nombre de tours avant arrêt : N1 = q 1 / (2p) = w0 t / (2p)

N1 = 157 * 0,631 / 6,28 = 15,7 tours.

Le théorème du moment cinétique appliqué à un solide en rotation autour d'un axe fixe s'écrit :

J dw /dt = Tf-lw soit Jw' + lw = Tf.(2)

solution générale de l'équation différentielle sans second membre :

w =A exp ( - lt / J)

solution particulière de (2) : w = Tf /l.

solution générale de (2) : w =A exp ( - lt / J)+ Tf /l. .

déterminer la constante sachant qu'à t = 0, la vitesse angulaire est w0 =Tm/ l

w0 = A+ Tf/ l. d'où A= w0 -Tf/ l.

w (t)=(w0 -Tf/ l) exp ( - lt / J)+ Tf /l .

à l'arrêt w = 0

0 =(w0 -Tf/ l) exp ( - t2 /t )+ Tf /l .

remplacer w0 par Tm/l et multiplier par l :

-Tf / (Tm-Tf ) = exp ( - t2 /t )

ln [Tf / (Tf-Tm ) ] = - t2 /t

t2 = t ln [(Tf-Tm ) / Tf ).

application numérique : t2 = 0,631 ln [(-1-3) / (-1)] = 0,631 ln 4 = 0,874 s.

nombre de tours effectués avant l'arrêt :

q 2 = (Tf t2 + t Tm ) / l.

N2 =q 2 / (2p)= (-1 *0,874 + 0,628 *3) / (0,019*6,28)= 8,46 tours.

retour - menu