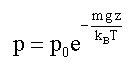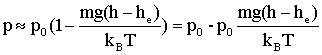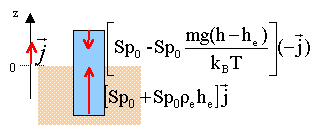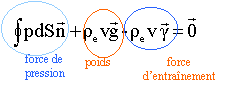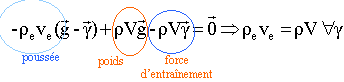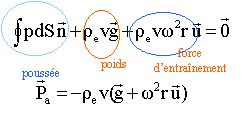|
référentiel non galiléen en translation référentiel non galiléen en rotation En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|
| .
. |
|
|
|
corrigé |
|
|
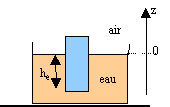
- la résultante des force de pression - l'opposée du poids du volume de liquide déplacé.
Le principe fondamental de l'hydrostatique donne la pression dans le plan z = - he : p(z= - he ) = p0 +re g he . La pression dans une atmosphère isotherme varie avec l'altitude selon la loi : (m : masse d'une molécule d'air)
sur la face supérieure du cylindre z = h-he. développement limité au premier ordre lorsque z est petit de l'exponentielle : e x voisin de 1+ x.
La poussée d'Archimède, résultante des forces de pression est alors : la résultante des forces de pression sur la face latérale du cylindre est nulle, il reste les forces de pression exercée par l'eau sur le fond de section S, par l'air sur le haut.
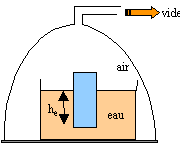
Pa = S[p0 +re g he ]+ S[p0 +p0 mg(h-he) / (kBT)] Pa = S[re g he + p0 mg(h-he) / (kBT)]. la loi des gaz parfaits s'écrit : PV= n RT M : masse molaire de l'air; ra : masse volumique de l'air avec n = m / M et m / V = ra ; d'où : P = ra RT / M = rakBT / m par suite la poussée s'écrit : Pa = S[re g he + ra g(h-he) ]. c'est à dire la somme des poids d'air et d'eau déplacés par le cylindre. Si on suppose la pression de l'air uniforme au voisinage du cylindre, cela revient à négliger la poussée d'Archimède due à l'air. La poussée d'Archimède n'existe qu'en présence d'un gradient de pression. A l'équilibre le poids du cylindre est opposée à la poussée. Si on fait le vide sous la cloche, la masse volumique de l'air décroît ; en conséquence la poussée d'Archimède due à l'air décroît. Pour maintenir l'équilibre la poussée due à l'eau doit augmenter et le cylindre va s'enfoncer.
|
|
|
référentiel non galiléen en translation : Le dispositif précédent est placé dans un ascenceur vertical uniformément accéléré vers le bas avec une accélération g
corrigé Dans le référentiel de l'ascenceur, en translation rectiligne par rapport à un référentiel terrestre, un petit volume v de liquide est en équilibre sous l'action : - de son poids ;- des forces de pression ;- de la force d'entrainement.
La poussée d'archimède est la résultante des forces de pression ; son module est égal au poids apparent du volume d'eau déplacé. Pa = rev (g - g ). La poussée due à l'air est négligée. L'équilibre du cylindre de volume total V, dans le repère de l'ascenceur s'écrit : ve est le volume du cylindre immergé.
Le cylindre reste en équilibre lorsque l'ascenceur se déplace.
|
|
|
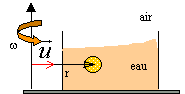
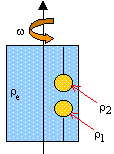
référentiel non galiléen en rotation : Le cristallisoir est fixé sur un plateau horizontal tournant autour d'un axe vertical avec une vitesse angulaire de rotation w constante. On désigne par r la distance du petit volume d'eau à l'axe de rotation.
corrigé Dans le référentiel de l'ascenceur, en rotation par rapport à un référentiel terrestre, un petit volume v de liquide est en équilibre sous l'action : - de son poids ;- des forces de pression ;- de la force d'entrainement. La force de Coriolis n'intervient pas à l'équilibre.
- la poussée d'Archimède centripète de module rev w2 r - la force d'entrainement centrifuge de module rv w2 r La
résultante radiale est : La sphère supérieure ( r2 >re) s'écarte de l'axe de rotation, alors que la sphère inférieure se rapproche de l'axe. L'effet est d'autant plus grand que les sphères sont plus éloignées de l'axe et que la vitesse de rotation est grande.
retour - menu |