Mathématiques,
suite, nombres complexes et fonctions
bac S Nlle Calédonie 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice 1. QCM ( 4 points).
Pour chacune des questions, une seule des quatre affirmations est
exacte. Aucune justification n’est demandée.
Une réponse exacte rapporte un point, une réponse fausse ou une absence
de réponse ne rapporte ni n’enlève aucun point.
1. Une variable aléatoire X suit la
loi normale de moyenne 100 et d’écart-type 36. On a alors, à 10−3 près
:
a. P(X < 81,2) ≈
0,542
b. P(X < 81,2) ≈
0,301. Vrai.
c. P(81,2 < X < 103,8) ≈0,542
P(X
< 81,2)
≈ 0,301 ; P(X
<
103,8) ≈ 0,542 ; P(81,2 < X < 103,8) ≈0,542 -0,301 ~0,241.
d. P(81,2 < X < 103,8) ≈0,301
2. Une variable aléatoire X suit la
loi normale de moyenne 50 et d’écart-type 2.
Une variable aléatoire N suit la loi normale centrée réduite. On a
alors :
a. P(X > 52) =(1−P(−2 < N < 2) ) / 2
b. P(X > 52) = 1−P(−2 < N < 2)
c. P(X > 52) =( 1−P(−1 < N < 1) ) / 2. Vrai.
d. P(X > 52) = 1−P(−1 < N < 1).
On pose N = (X-50) / 2 =
(52-50) / 2 = 1.
P(X >
52) =P(N > 1) = P(N < -1).
P(-1 < N < 1) =
1-P(N<-1)-P(N>1) = 1-2 P(N >1) ; P(N >1) = (1-P(-1 < N
<1) ) / 2.
3. Une variable aléatoire T suit une
loi exponentielle telle que P(T > 2) = 0,5.
Une valeur approchée à 10−2 près de la probabilité P(T>2)(T
> 5) est égale à :
a. 0,35. Vrai.
b. 0,54
c. 0,53
d. e / 2.
La loi exponentielle est
sans vieillissement : P(T>2)(T > 5) = P(T > 5-2) = P (T > 3).
P(T >3) < P(T
>2) donc P(T >3) < 0,5.
4. Une urne contient 5 boules bleues
et 3 boules grises indiscernables au toucher. On tire successivement de
manière indépendante 5 boules avec remise dans cette urne. On note
alors X la variable aléatoire comptant le nombre de boules grises
tirées.
On note E(X) l’espérance de X. On a alors :
a. E(X)= 3
b. E(X)= 3 / 8
c. P(X >1) ≈ 0,905
à 10−3 près. Vrai.
d. P(X >1) ≈ 0,095
à 10−3 près.
Probabilité de tirer une
boule grise : 3 / 8 =0,375 ; X suit la loi binomiale de
paramètres n = 5 et p = 0,375.
P(X > 1) = 1-P(X=0) = 1-C05 x0,3750
x(1-0,375)5 =1-(1-0,375)5
~0,905.
Exercice 2. Nombres
complexes (5 points).
Soient les deux nombres complexes :
z1 = 1−i et z2 = −8−8 x 3½i.
On pose : Z =z1 / z2.
1. Donner la forme
algébrique de Z.
2. Écrire z1
et z2 sous forme exponentielle.
3. Écrire Z sous
forme exponentielle puis sous forme trigonométrique.
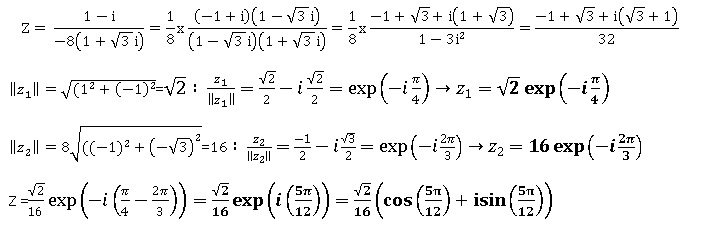
4. En déduire que
cos(5p/12)=(6½-2½)
/ 4.
On compare les parties réelles dans les deux écritures de Z :
2½ / 16 cos(5p/12) =(-1+3½) /
32 ; cos(5p/12) =(-1+3½) / (2 x2½) ;
puis multiplier numérateur et dénominateur par 2½.
5. On admet que : sin(5p/12)=(6½+2½)
/ 4.
• pour tous réels a et b, cosa cosb −sina sinb = cos(a +b).
Résoudre l’équation suivante dans l’ensemble des réels R :
(6½-2½) cos x- (6½+2½)
sin x = -2*3½.
(6½-2½)
/ 4 cos x- (6½+2½) / 4 sin x =
-3½/ 2
cos(5p/12) cos x -sin(5p/12) sin x = -3½/ 2
cos(5p/12
+x) = -3½/ 2=
cos (5 p / 6).
5p/12
+x = ±5
p / 6+
2kp.
x = ±5 p
/ 6 -5p/12
+ 2kp.
x = 5 p /12 + 2kp et x =
-5p/4 + 2kp avec k entier relatif.
|
|
.
.
|
|
|
Exercice
3 ( 5 points).
Pour chacune des affirmations proposées, indiquer si elle est VRAIE ou
FAUSSE et justifier cette réponse.
Une réponse non justifiée ne sera pas prise en compte.
1. Soit la suite (un)
définie pour tout entier naturel n par
u0 = 14
un+1 = 2un −5.
Soit la suite (tn) définie pour tout entier naturel n par
tn = un −5.
Affirmation
A : La suite (tn) est une suite géométrique. Vrai.
tn+1 =
un+1 -5 =
2un −10=2(un-5) =2 tn.
La suite (tn) est géométrique de raison q = 2 et de premier terme
t0=14-5 = 9.
Affirmation B
: Pour tout entier naturel n, un = 9×2n +5. Vrai.
Initialisation
: la propriété est vraie au rang zéro.
Hérédité :
la propriété est supposée vraie au rang p : up = 9×2p
+5.
up+1=
2(9x2p+5)-5=9x2p+1+5 .
Conclusion
: la propriété est vraie au rang zéro et héréditaire, elle est vraie
pour tout entier naturel.
2.
Soit une suite (vn).
Affirmation
C : Si, pour tout entier naturel n supérieur à 1,
−1−1 / n < vn
< 1+1 /
n
alors la suite (vn) converge.
Faux.
Soit une suite (vn) définie par vn = (-1)n
/ 2 ; vn vérifie bien
−1−1 / n < vn
< 1+1 /
n mais elle ne converge pas
3. Affirmation D
: Pour tout entier naturel n non nul, (8×1+3)+(8×2+3)+. . . +(8×n +3)
=n(4n +7). Vraie.
(8×1+3)+(8×2+3)+. .
. +(8×n +3) =8 (1 +2 +... +n)+ 3n =8 x 0,5 n (n+1) + 3n = 4 n(n+1)+3n =
n(4n+4+3) =n(4n+7).
4. Soit (wn) une suite
convergente.
Affirmation
E : Si, à partir d’un certain rang, tous les termes de la suite
(wn) sont strictement positifs,
alors la limite de la suite (wn) est aussi strictement
positive. Faux.
Soit la suite (wn) = 1 / n. Tous ses termes sont strictement
positifs ; la suite converge vers zéro.
|
|
|
|
Exercice 4 ( 6 points).
Soit R l’ensemble des nombres réels.
Partie A
Soit g la fonction définie et dérivable sur R telle que, pour tout réel
x,
g(x) = −2x3+x2−1.
1. a. Étudier les
variations de la fonction g.
b. Déterminer les
limites de la fonction g en −∞et en +∞.
g '(x) = -6x2 +2x = 2x(1-3x).
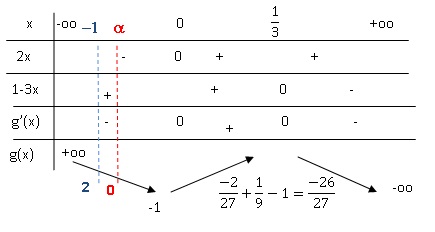
2. Démontrer que
l’équation g(x) = 0 admet une unique solution dans R, notée α, et que α
appartient à [−1 ; 0].
D'après le tableau de variation ci-dessus, l'équation g(x) = 0 admet
une seule solution sur R, que α appartient à [−1 ; 0].
3. En déduire le
signe de g sur R.} -oo ; a ], g est positive.
Si x appartient à ] -oo ; a [, g est positive.
Si x appartient à ] a ; +oo[, g est négaitive.
Partie B
Soit f la fonction définie et dérivable sur R telle que, pour tout réel
x,
f (x) =(1+x +x2 + x3)e−2x+1.
On note f ′ la fonction dérivée de la fonction f sur R.
1. Démontrer que
f(x) tend vers moins l'infini si x tend vers moins l'infini.
Quand x tend vers moins l'infini : e−2x+1 tend vers plus
l'infini ;
la limite du polynome est celle de son terme de plus haut degré :
(1+x +x2 + x3) tend vers moins l'infini.
Faire le produit des limites : f(x) tend vers moins l'infini.
2. a. Démontrer
que, pour tout x >1, 1 < x < x2 < x3.
Multiplier l'inégalité x >1 par x strictement positif : x2
> x ;
multiplier cette nouvelle inégalité par x strictement positif
: x3 > x2 ;
par
suite, pour tout x >1, 1 < x < x2 < x3.
b.
En déduire que, pour x > 1, 0 < f(x) < 4x3e−2x+1.
Pour tout x >1, 1 < x < x2 < x3,
donc 0 <1+x+x2 +4x3 < 4x3.
De plus e−2x+1 est toujours positif.
Donc 0 <(1+x +x2 + x3)e−2x+1< 4x3e−2x+1 soit
0 < f(x) < 4x3e−2x+1.
c.
On admet que, pour tout entier naturel n, la limite de xn e-x
est égale à zéro si x tend vers plus l'infini.
Vérifier que, pour tout réel x, 4x3e−2x+1=
½e
(2x)3e−2x puis montrer que 4x3e−2x+1 tend vers
zéro quand x tend vers plus l'infini.
4x3e−2x+1=4x3e−2x e =8 x3e−2x e /
2 =( 2x)3e−2x e /2 ;
on pose X = 2x ; X3 e-X tend vers zéro quand X
tend vers plus l'infini.
Par suite 4x3e−2x+1 tend vers
zéro quand x tend vers plus l'infini.
d. On note C la
courbe représentative de f dans un repère orthonormé.
En utilisant la question précédente, déterminer la limite de f en plus
l'infini et en donner une interprétation graphique.
Si x > 1, alors 0 < f(x) < 4x3e−2x+1.
De plus, 4x3e−2x+1 tend vers
zéro quand x tend vers plus l'infini.
D'après le théorème des gendarmes, f(x) tend vers zéro quand x tend
vers plus l'infini.
L'axe des abscisses est asymptote à la courbe C.
3. Démontrer que,
pour tout x de R, f ′(x) =(-2x3+x2-1)e-2x+1.
On pose u
=1+x +x2 + x3 et v = e−2x+1 ; u ' =
1+2x+3x2 ; v ' = -2 e-2x+1.
u'v +v'u = (1+2x+3x2 )e−2x+1 -2e−2x+1
(1+x +x2 + x3) = e−2x+1 (-1 +x2
-2 x3) = g(x )e−2x+1.
4.
À l’aide des résultats de la partie A, déterminer les variations de f
sur R.
e−2x+1
est toujours positif.
Si x appartient à ] -oo ; a [, g est positive : f '(x) est positive et
f est strictement croissante.
Si x appartient à ] a ; +oo[, g est négaitive : f '(x) est
négative et f est strictement décroissante.
|
|
|