Mathématiques,
suites, nombres complexes, fonctions, géométrie dans l'espace.
Bac S Antilles 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1.
On muni le plan complexe d'un repère orthonormé direct. On considère
l'équation (E) :
z 4 +2z 3 -z-2=0
ayant pour inconnue le nombre complexe z.
1. Donner une
solution entière de (E).
1 4+2 x1 3 -1-2 = 0 est vérifiée.z = 1.
2. Démontrer que
pour tout complexe z :
z4 +2z3 -z-2=(z2+z-2)(z2+z+1).
(z2+z-2)(z2+z+1)= z4
+z3+z2
+z3 +z2+z-2z2-2z-2
= z4 +2z3 -z-2.
3. Résoudre (E)
dans l'ensemble des nombres complexes.
z2+z-2=0 ;
discriminant D =12+4
x 2=9 ; racine carrée du discriminant : 3.
Solutions z1 = (-1+3) / 2 =1
et z2 =(-1-3)/2 = -2.
z2+z+1=0
; discriminant D
=12-4 =-3 =3i2 ; racine carrée du discriminant : 3½i.
Solutions z3 = (-1+3½i)
/ 2 et z4 =(-1-3½i)/2
.
4. Les solutions de
l'équation (E) sont les affixes de 4 points A, B, C, D du plan complexe
tes que ABCD est un quadrilatère non croisé.
Le quadrilatère est-il un losange ? Justifier.
Soient Les pointys :
A d'affixe 1, B d'affixe (-1+3½i) / 2,
C d'affixe -2 et D d'affixe (-1-3½i)
/ 2.
Les nombres complexes (-1+3½i)
/ 2 et (-1-3½i) / 2
sont conjugués ; donc la droite (BD) est perpendiculaire à l'axe des
réels.
Les nombres complexes 1 et -2 appartiennent à l'axe des réels ; donc la
droite (AC) est perpendiculaire à la droite (BD).
Les diagonales du quadrilatère ABCD sont perpendiculaires.
Affixe du milieu du segment [AC] : [(-1+3½i) / 2 +(-1-3½i) / 2] / 2 = -0,5.
Affixe du milieu du segment [BD] : (1-2) / 2 = -0,5.
Les diagonales du quadrilatère se coupent en leur milieu.
Le quadrilatère ABCD est donc un losange.
Exercice 2.
Dans une usine automobile, certaines pièces métalliques sont
recouvertes d’une fine couche
de nickel qui les protège contre la corrosion et l’usure. Le procédé
utilisé est un nickelage par
électrolyse.
On admet que la variable aléatoire X, qui à chaque pièce traitée
associe l’épaisseur de nickel
déposé, suit la loi normale d’espérance µ1 = 25 micromètres
(μm) et d’écart type σ1.
Une pièce est conforme si l’épaisseur de nickel déposé est comprise
entre 22,8 μm et 27,2 μm.
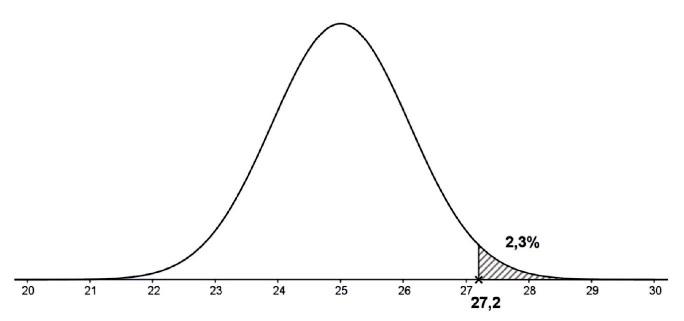
La fonction de densité de probabilité de X est représentée ci-dessous.
On a pu déterminer que P(X >27,2) = 0,023.
1. a. Déterminer la
probabilité qu’une pièce soit conforme.
P(22,8 < X < 27,2) = 1-0,023-0,023 =0,954.
b. Justifier que
1,1 est une valeur approchée de s1
à 10−1 près.
Le cours indique que lorsque X suit la loi normale d'espérance µ et
d'écart type s,
P(µ-2s1 < X < µ+2s1)=0,954.
22,8 = µ-2,2 ; 27,2 =µ+2,2.
2s1 =
2,2 ; s1 =
1,1.
c. Sachant qu’une pièce est
conforme, calculer la probabilité que l’épaisseur de
nickel déposé sur celle-ci soit inférieure à 24 μm. Arrondir à 10−3.
P(22,8 < X < 27,2)(X
<24)=[ P(X <24)
n ( 22,8 < X <27,1)] / P( 22,8 < X <27,1).
P(22,8 < X < 27,2)(X <24)= P(
22,8 < X < 24) / P(
22,8 < X <27,1).
P(22,8
< X < 27,2)(X
<24)=0,1589 / 0,954 = 0,167.
2.
Une équipe d’ingénieurs propose un autre procédé de nickelage, obtenu
par réaction chimique sans aucune source de courant. L’équipe affirme
que ce nouveau procédé permet théoriquement d’obtenir 98 % de pièces
conformes.
La variable aléatoire Y qui, à chaque pièce traitée avec ce nouveau
procédé, associe
l’épaisseur de nickel déposé suit la loi normale d’espérance µ2
= 25 μm et d’écart-type s2.
a. En admettant
l’affirmation ci-dessus, comparer s1 et s2.
L'espérance mathématique est identique ; Dans le second procédé, la
probabilité qu'une pièce soit conforme est 0,98, supérieure à celle du
premier procédé.
Donc s2
<s1.
b. Un contrôle
qualité évalue le nouveau procédé ; il révèle que sur 500 pièces
testées, 15 ne sont pas conformes. Au seuil de 95 %, peut-on rejeter
l’affirmation de l’équipe d’ingénieurs ?
n =500 > 30 ; p = 0,98 soit np
= 500 x0,98 = 490 >
5 ; q = 1-p = 0,02 soit nq = 500 x0,02 = 10 > 5.
Les conditions sont respectées pour définir un intervalle de
fluctuation asymptotique au seuil de 95 %.
1,96 x(pq / n)½ =1,96 x(0,98 x0,02 / 500)½ =
0,0123.
Intervalle de fluctuation : [0,98 -0,0123 ; 0,98 +0,0123 ] soit [0,968
; 0,992].
485 pièces sont conformes sur 500 ; la fréquence observées est :
485 / 500 = 0,97.
Cette valeur appartient à l'intervalle de fluctuation.
Au seuil de 95 %, on ne peut pas rejeter l'affirmation des ingénieurs.
|
| .
. |
....
.....
|
Exercice
3.
Soient f et g les fonctions définies sur l’ensemble R des nombres réels
par
f(x) = ex et g(x)= e−x.
On note Cf la courbe représentative de la fonction f et Cg
celle de la fonction g dans un
repère orthonormé du plan.
Pour tout réel a, on note M le point de Cf d’abscisse a et N
le point de Cg d’abscisse a.
La tangente en M à Cf coupe l’axe des abscisses en P, la
tangente en N à Cg coupe l’axe des
abscisses en Q.
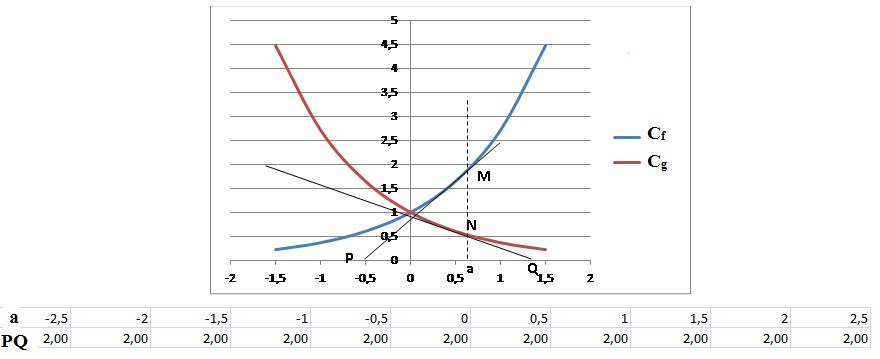
À l’aide d’un logiciel de géométrie dynamique, on a représenté la
situation pour différentes
valeurs de a et on a relevé dans un tableur la longueur du segment [PQ]
pour chacune de ces
valeurs de a.
1. Démontrer que la
tangente en M à Cf est perpendiculaire à la tangente en N à Cg.
Coefficient directeur de la tangente à Cf en M d'abscisse a
: f '(a) = ea.
Cette tangente passe en M ( a ; ea).
Equation de cette tangente : y = eax +b ; ea = a ea
+b ; b = ea(1-a) ; y = eax
+ea(1-a)
Coefficient directeur de la
tangente à Cg en N d'abscisse a : g '(a) = -ea.
Cette tangente passe en N ( a ; e-a).
Equation de cette tangente : y = -e-ax +b' ; e-a
= -a e-a +b' ; b' = e-a(1+a) ; y = -e-ax +e-a(1+a).

2.a.
Que peut-on conjecturer pour la longueur PQ ?
PQ = 2 = constante.
b. Démontrer cette
conjecture
yP=0 ; xP = a-1 ; yQ=0 ; xQ
= a+1 ;
PQ = |xQ -xP |= |a+1-(a-1)| =2. |
|
|
Exercice 4.
Dans tout l'exercice, n désigne un entier naturel strictement positif.
Le but de l’exercice est d’étudier l'équation
(En) : ln(x) /x =1 / n
ayant pour inconnue le nombre réel strictement positif x.
Partie A.
Soit f la fonction définie sur l’intervalle ]0 ; + ∞[ par
f(x) =ln(x) / x.
On admet que la fonction f est dérivable sur l’intervalle ]0
; + ∞[.
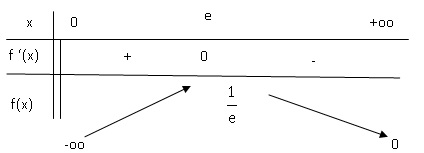
1. Étudier
les variations de la fonction f.
2.
Déterminer son maximum.
Calcul de la dérivéef
'(x). On pose u = ln(x) ; v = x ; u' = 1/x et v' = 1.
f '(x) =(u'v-v'u)/ v2 = (1-ln(x) / x2.
Le signe de f '(x) est celui de 1-ln(x).
f '(x) est positive si x < e; f(x) est strictement croissante sur ]0
; e[.
f '(x) est négative si x > e ; f(x) est strictement décroissante sur
]e ; +oo[.
f '(x) = 0 si x = e ; f(x) présente un maximum pour x = e ; ce maximum
vaut f(e) = 1 /e = e-1.
|
|
|
|
Partie B.
1. Montrer que,
pour n ≥ 3, l'équation f(x) = 1/n possède une unique solution sur
[1 ; e] notée an.
Sur l'intervalle [1 ; e], f(x) est continue ( car dérivable) ; de plus
f(x) est strictement croissante.
f(1) =0 < 1 / n ; f(e) = 1 /e~0,37 > 1/ n.
D'après le théorème des valeurs intermédiaires, l'équation f(x) = 1 / n
admet une solution unique sur [1 ; e].
2. D’après ce qui
précède, pour tout entier n ≥ 3, le nombre réel an est solution de
l’équation (En).
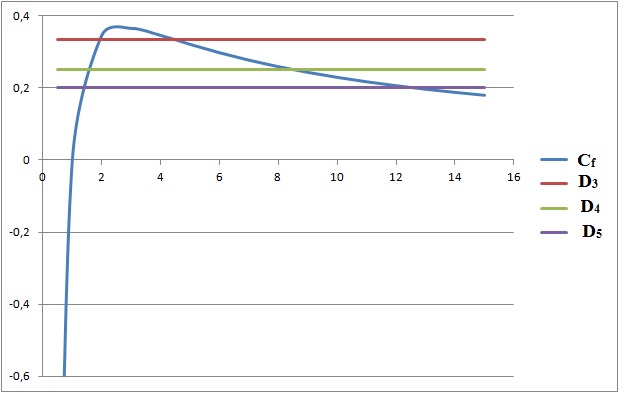
a. Sur le graphique
sont tracées les droites D3, D4 et D5
d’équations respectives
y = 1 /3 ; y = 1 / 4 et y = 1 / 5.
Conjecturer le sens de variation de la suite (an).
Sur le graphe, on lit a3
> a4
>a5.
La suite (an)
semble décroître.
b.
Comparer, pour tout entier n ≥ 3, f(an)
et f(an+1).
Déterminer le sens de variation de la suite (an).
f(an)
= 1 / n ; f(an+1)
= 1 / (n+1).
1 / (n+1) < 1 / n, donc f(an)
>f(an+1).
La fonction f est strictement croissante sur [1 ; e] par conséquence an)
>an+1.
La suite (an)
est par conséquent décroissante.
c.
En déduire que la suite (an)
converge.
Il n’est pas demandé de calculer sa limite.
La suite (an)
est décroissante et minorée par 1. Donc elle converge.
3. On admet que, pour tout entier n ≥ 3,
l’équation (En) possède une autre solution ßn
telle que
1 ≤ an
≤ e ≤ ßn .
a. On admet que la
suite (ßn) est croissante.
Établir que, pour tout entier naturel n supérieur ou égal à 3,
ßn ≥ nß3 / 3.
D'une part ln(ßn) / ßn = 1 /n ;
ln(ßn) =
ßn /n ;
d'autre part la suite (ßn) est
croissante.
En conséquence pour tout entier supérieur à 3 :
ßn > ß3,
par suite ln (ßn) >
ln(ß3), la fonction ln étant strictement croissante sur ]0 ;
+oo[.
Par suite ßn / n >
ß3 / 3 ; ßn
>
n ß3 / 3.
b.
En déduire la limite de la suite (ßn).
ß3 >0 ; la limite de n
ß3 / 3, quand n tend vers l'infini, est égale à l'infini.
Or ßn
>
n ß3 / 3 ; d'après le théorème de comparaison la
limite de ßn , quand n tend vers
l'infini, est égale à l'infini.
|
Exercice 5.
On note R l’ensemble des nombres réels.
L'espace est muni d'un repère orthonormé (O, i, j, k).
On considère les points A(−1; 2; 0), B(1; 2; 4) et C(−1; 1; 1).
1.a. Démontrer que
les points A, B et C ne sont pas alignés.
b. Calculer le
produit scalaire suivant.
c. En déduire la
mesure de l’angle BAC , arrondie au degré.
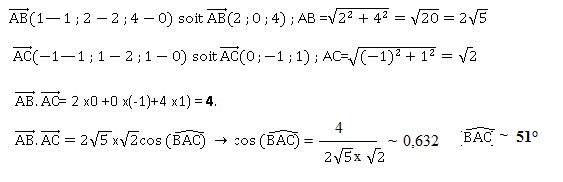
2. Soit n le
vecteur de coordonnées (2 ; -1 ; -1).
a. Démontrer que ce
vecteur est un vecteur normal au plan (ABC).
b. Déterminer une
équation cartésienne du plan (ABC).
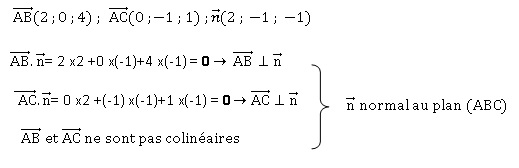
Equation cartsienne du plan (ABC) : 2x -y -z +d =0.
Les coordonnées du point A vérifient cette équation : 2(-1)-2-0+d=0
soit d = 4.
Par
suite : 2x -y -z +4 =0.
3. Soient p1 le plan
d'équation 3x + y − 2z + 3 = 0 et p2 le plan passant par O
et parallèle au plan d'équation x -2z + 6 = 0.
a. Démontrer que le
plan p2 a pour équation x=2z.
L'équation cartésienne du plan p2 est de la forme
x-2z+d=0.
Les coordonnées du point O(0 ; 0 ; 0) vérifient cette équation :
0-2x0+d = 0 soit d =0 ;
par suite : x-2z=0
ou x = 2z.
b. Démontrer que
les plans p1 et p2 sont sécants.
Un vecteur normal au plan p1 a pour coordonnées (3 ; 1 ; -2).
Un
vecteur normal au plan p2 a pour coordonnées (1 ; 0 ; -2).
Ces deux vecteurs ne sont pas colinéaires. Donc les
plans p1 et p2 sont sécants.
c. Soit la droite D dont un système
d'équations paramétriques est
x=2t ; y=-4t-3 ; z=t avec t réel.
Démontrer que D est l’intersection des plans p1 et p2.
Pour tout réel t : 3(2t)+(-4t-3)-2t+3=6t-6t-3+3=0 ; donc D est incluse
dans p1.
Pour
tout réel t : 2t -2t=0 ; donc D
est incluse dans p2.
Ces deux plans étant sécants suivant une droite, cette droite ne peut
être que la droite D.
4. Démontrer que la droite D coupe
le plan (ABC) en un point I dont on déterminera les coordonnées.
Il faut résoudre le système :
x=2t ; y=-4t-3
; z=t et 2x -y
-z +4 =0.
4t-(-4t-3)-t+4=0 ; 7t +7=0 ; t = -1.
Par suite x =-2 ; y =4-3 = 1 ; z = -1.
La droite D et le plan ABC n'ont qu'un seul point commun obtenu pour t
=-1.
Les coordonnées de ce point sont I(-2 ; 1 ; -1).
|
|