Mathématiques,
probabilités, fonction, géométrie, bac
S Polynésie 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice
1.
Une société fournit des abonnements internet et des
abonnements de téléphone mobile. Un client souscrit soit un abonnement
internet, soit un abonnement téléphone mobile, il ne cumule pas les
deux. Sur la ligne d'assistance téléphonique, le client doit d'abord
signaler s'il est client internet ou s'il est client mobile. puis son
appel est mis en attente de réponse par un opérateur.
A. Durée d'attente.
1. On s'interesse à
la durée d'attente d'un client internet lorsqu'il contact l'assistance
téléphonique avant de joindre un opérateur. Cette durée d'attente en
minute est modélisée par une varaible aléatoire D 1 qui suit
la loi exponentielle de paramètre 0,6.
a. Quelle est la
durée moyenne d'attente ?
1 / l = 1 /0,6 =
1,667 minutes ou 1 min 40 s.
b. Calculer la
probabilité que la durée d'attente soit inférieure à 5 minutes.
P(D 1 <
5) = 1-exp(-0,6 x5) = 0,950.
2. On s'intéresse à
la durée d'attente d'un client mobile lorsqu'il contact l'assisatnce
avant de joindre un opérateur. Cette durée est modélisée par une
variable aléatoire D 2 qui suit une loi exponentielle de
paramètre l >0.
a. Sachant que P(D 2
< 4)
=0,798, déterminer l.
1-exp(-4 l) = 0,798
; exp(-4 l) =
1-0,798 = 0,202.
-4 l = ln(0,202) ; l ~ 0,4.
b. En prenant l =
0,4, peut-on considérer que moins de 10 % des clients mobiles choisis
au hasard attendent plus de 5 minutes avant de joindre un opérateur.
P(D 2 >
5 ) =exp(-0,4 x5) = 0,1353 ( 13,5 %).
13,5 % des
clients mobiles choisis au hasard attendent plus de 5 minutes avant de
joindre un opérateur.
B. Obtention d'un opérateur.
Si la durée d'attente avant l'obtention d'un opérateur dépasse 5
minutes, l'appel prend automatiquement fin. Sinon, l'appelant obtient
un opérateur.
On choisit au hasard un client qui appelle la ligne d'assistance. On
admet que la probabilité que l'appel émane d'un client internet est
0,7.
Si l'appel émane d'un client internet alors la probabilité d'obtenir un
opérateur est égale à 0,95.
Si l'appel
émane d'un client mobile alors la probabilité d'obtenir un opérateur
est égale à 0,87.
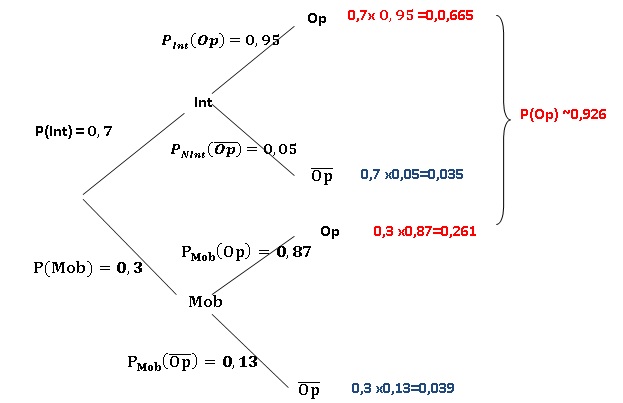
1. Déterminer la
probabilité qu'un client joigne un opérateur.
b. Un client se
plaint que son appel a pris fin au bout de 5 minutes d'attente sans
avoir obtenu d'opérateur. Est-il plus probable que se soit un client
internet ou un client mobile ?
Probabilité que l'appel prenne fin au bout de 5 minutes d'attente pour
un client :
- internet : 0,035
- mobile 0,039.
Il est probable que ce soit un client mobile.
C. Enquète de
satisfaction.
La société annonce un taux de satisfaction de 85 % pour ces clients
ayant appelé et obtenu un opérateur. Une association de consommateurs
souhaite vérifier ce taux et interroge 1303 clients. parmi celles-ci
1150 se disent satisfaites. Que pensez-vous du taux de satsifaction
annoncé par la société ?
n =1303 >30 ; p =
0,85 soit np = 1303 x0,85=1107,55 > 5.
nq = n(1-p) = 1303 x0,15 = 195,45 >5.
Au seuil de confiance de 95%, on détermine un
intervalle de fluctuation asymptotique :
1,96 (pq / n)½ = 1,96 x(0,85 x0,15 /1303)½
=0,0194.
[0,85-0,0194 ; 0,85+0,0194 ] soit [0,830 ; 0,869].
La fréquence observée est égale à 1150 /1303 ~0,883, n'appartient pas à
l'intervalle de fluctuation.
Le taux de satisfaction annoncé est trop faible, au risque de 5 %.
|
| .
. |
....
.....
|
Exercice 2 .
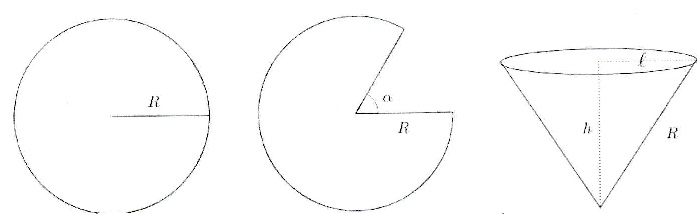
Dans un disque en carton de rayon R
on découpe un secteur angulaire correspondant à un angle a. On supperpose les bords
du disque afin d'obtenir un cône de révolution. On souhaite choisir a afin d'avoir un cône de
volume maximal.
1. On choisit R = 20 cm.
a. Montrer que le volume du cône en
fonction de sa hauteur h est V(h) = p /3 (400-h2)h.
Volume d'un cône : V = 1 / 3 surface de base fois hauteur.
Surface de base : p(R2-h2)
= p(400 -h2).
Par suite V(h) = p /3 (400-h2)h.
b. Justifier qu'il existe une valeur
de h qui rend le volume du cône maximum. Donner cette valeur.
V '(h) = p /3 (400-3h2).
V '(h) = 0 pour h = 20 / 3½.
Si h < 20 / 3½ , la
dérivée V '(h) est positive et V(h) est croissante.
Si h > 20 / 3½
, la dérivée V '(h) est négative et V(h) est décroissante.
Il s'agit donc d'un maximum.
c. Comment découper le disque pour
avoir un volume maximum ? Donner un arrondi de a au degré près.
On note r le rayon de la base du cône ; r = (R2-h2)½
;
l = 2p r = (2p-a)R ; a = 2p (1-r / R).
Le
volume est maximal si h2 = 400 / 3 ; r = (R2-400 /3)½
;
Or R = 20 cm ; r = (202-400 /3)½
= 20 x2½ / 3½~16,33 cm.
a = 2p (1-r / R)~2p (1-16,33 / 20)~0,367 p radian ou 66°.
b. L'angle a dépend-il du rayon R du
disque en carton ?
Non : a = 2p (1-r / R) avec r = (R2-h2)½
et h2=R2/3.
r = (R2-R2/3)½
= (2R2/3)½
=R x(2 / 3)½ ; r / R = (2 / 3)½
;
a = 2p (1- (2 / 3)½).
Exercice 3.
L'objectif est de déterminer une mesure de l'angle entre deux liaisons
carbone-hydrogène dans la molécule de méthane.
Un tétraèdre régulier est un polyèdre dont las quatre faces sont des
triangles équilatéraux.
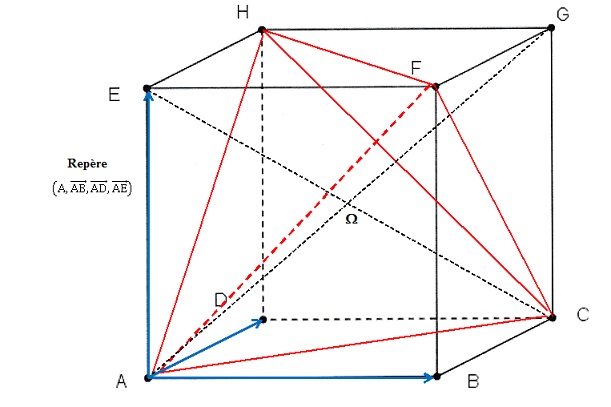
1. Justifier que
l'on peut inscrire ce tétraèdre dans un cube ABCDEFGH en positionnant 2
atomes d'hydrogène sur les sommets A et C du cube et les deux autres
atomes d'hydrogène sur deux autres sommets du cube. Représenter la
molécule dans le cube donné.
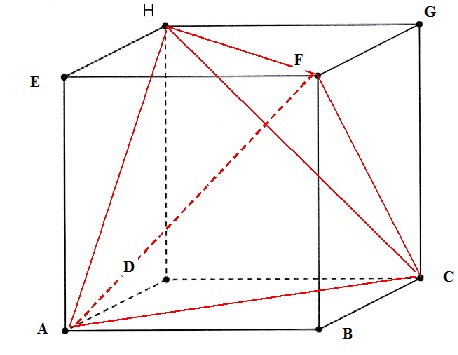
Tous les segments rouges ont même mesure celle de la diagonale d'un
carré.
Les triangles ACH, CHF, AFH et ACF sont équilatéraux.
|
|
|
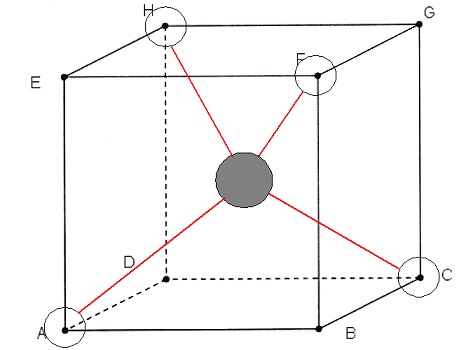
On travaillera dans
le repère indiqué ci-dessous.
2. Démontrer que l'atome de carbone
est au centre W
du cube.
Toutes les distances carbone-hydrogène sont égales.
Le centre du cube est à égale distance des sommets du cube.
W( 0,5
; 0,5 ; 0,5).
3. Déterminer
l'arrondi au dixième de degré de la mesure de l'angle que forment entre
elles les liaisons carbone-hydrogène.
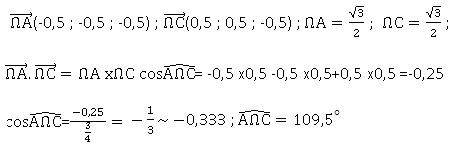
|
|
|
|
Exercice4.
On
s'intéresse à la chute d'une goutte d'eau qui se détache d'un nuage
sans vitesse initiale.
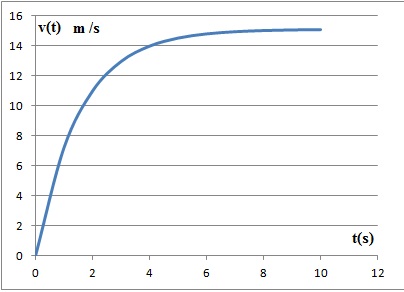
Un modèle simplifié donne la vitesse verticale de chute ( en m /s) en
fonction du temps.
v(t) = 9,81 m / k (1-exp(-kt /m)).
m : masse de la goutte en mg ; k >0 coefficient lié au frottement de
l'air.
A. Cas général.
1. Déterminer les
variations de la vitesse de la goutte.
v '(t) = 9,81 m /k (-k /m)(-exp(-kt /m)) =9,81exp(-kt /m).
La dérivée étant strictement positive sur [0 ; +oo[, la vitesse est
strictement croissante.
2. La goutte
ralentit-elle au cours de sa chute ?
Non, la vitesse initiale est nulle ; la vitesse limite vaut 9,81 m /k
et v(t) est strictement croissante.
3. Montrer que la
vitesse limite de chute est Vlim = 9,81 m / k.
Quand t tend vers l'infini, kt / m étant positif, le terme en
exponentielle tend vers zéro.
Par suite la vitesse tend vers 9,81 m / k.
4. Un scientifique
affirme qu'au bout d'une durée de chute égale à 5m /k, la vitesse de la
goutte dépasse 99 % de sa vitesse limite. Cette affirmation est-elle
correcte ?
exp(-k / m x 5m / k) = exp(--5) ; v(5m /k) = 9,81 m /k (1-e-5)
~0,993 x9,81 m /k ~0,993 Vlimite.
L'affirmation est correcte.
|
B. On prend m =6 et
k =3,9.
A un instant donné v(t) = 15 m /s.
1. Depuis combien
de temps la goutte s'est-elle détachée de son nuage ? Arrondir le
résultat au dixième de seconde.
v(t)
= 9,81 x 6 / 3,9 (1-exp(-3,9 t / 6)) =15,092 (1-exp(-0,65 t)) = 15 ;
.1-exp(-0,65 t) = 15 / 15,092
~0,99389 ; exp(-0,65 t)
=0,006116.
-0,65 t = ln(0,006116) = -5,0968 ; t ~7,84 s ; t ~7,8 s.
2.
En déduire la vitesse moyenne de cette goutte entre le moment où elle
s'est détachée du nuage et l'instant où est mesurée sa vitesse.
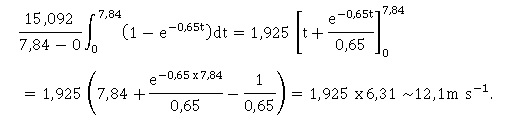
|
|