Mathématiques,
fonctions , bac S 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Liban
Soit
k un réel strictement positif. On considère les fonctions fk
définies sur R par :
fk(x) = x +k e-x .
On note Ck la courbe représentative de la fonction fk
dans un plan muni d’un repère orthonormé.
On a représenté ci-dessous quelques courbes Ck pour
différentes valeurs de k.
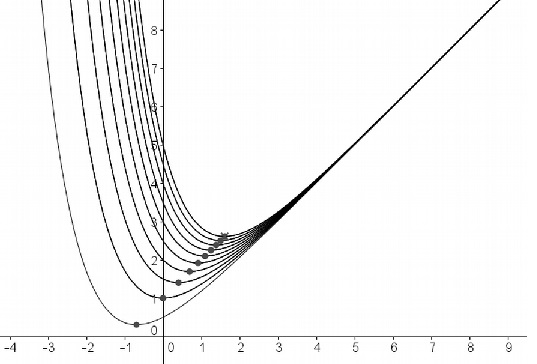
Pour tout réel k strictement positif, la fonction fk admet
un minimumsur R. La valeur en laquelle
ce minimum est atteint est l’abscisse du point noté Ak de la
courbe Ck. Il semblerait que, pour
tout réel k strictement positif, les points Ak soient
alignés. Est-ce le cas ?
f 'k =1 -ke-x =0 ; ex = k ; x = ln k.
fk (ln k) = lnk +1.
Coordonnées des points Ak : (ln k ; ln k+1).
Ces points appartiennent à la droite d'équation y = x+1. Ils sont donc
alignés.
Exercice 4.
L’épicéa commun est une espèce d’arbre résineux qui peut mesurer
jusqu’à 40 mètres de hauteur
et vivre plus de 150 ans. L’objectif de cet exercice est d’estimer
l’âge et la hauteur d’un épicéa à partir du diamètre de son tronc
mesuré à 1,30 m du sol.
Partie A
-Modélisation de l’âge d’un épicéa
Pour un épicéa dont l’âge est compris entre 20 et 120 ans, on modélise
la relation entre son âge (en
années) et le diamètre de son tronc (en mètre) mesuré à 1,30 m du sol
par la fonction f définie sur
l’intervalle ]0 ;1[ par : f (x) = 30ln((20x) / (1-x))
où x désigne le diamètre exprimé en mètre et f (x) l’âge en années.
1. Démontrer que la
fonction f est strictement croissante sur l’intervalle ]0 ;1[.
On pose u = 20 x et v = 1-x ; u' = 20 ; v' = -1 ; (u'v-v'u) /v2
=(20(1-x)+20x) / (1-x)2=20 / (1-x)2.
f '(x) =30 [20
/ (1-x)2.]
/ [20x)
/ (1-x ] =30 /((1-x)x).
x étant compris entre ]0 ;1[., f 'x) est positive sur cet
intervalle ; f(x) est strictement croissante sur cet intervalle.
2.
Déterminer les valeurs du diamètre x du tronc tel que l’âge calculé
dans ce modèle reste conforme à ses conditions de validité,
c’est-à-dire compris entre 20 et 120 ans.
20 = 30 ln(20x /(1-x)) ; e2/3 =
20x /(1-x) ; e2/3 (1-x)= 20x.
x(20 e-2/3+1)=1 ; x = 1 / (20 e-2/3+1)
=0,0887 ~0,09 m.
120 = 30
ln(20x /(1-x)) ; e4 = 20x /(1-x) ; e4
(1-x)= 20x.
x(20 e-4+1)=1 ; x = 1 / (20
e-4+1) =0,7318 ~0,74 m.
Le diamètre doit être compris entre 0,09 m et 0,73 m.
|
| .
. |
....
.....
|
Amérique du Nord.
Un
fabricant doit réaliser un portail en bois plein
sur mesure pour un particulier. L’ouverture du
mur d’enceinte (non encore construit) ne peut excéder 4 mètres de
large. Le portail est constitué
de deux vantaux de largeur a telle que 0 < a < 2.
Dans le modèle choisi, le portail fermé a la forme illustrée par la
figure ci-dessous. Les côtés [AD] et [BC] sont perpendiculaires au
seuil [CD] du portail.
Entre les points A et B, le haut des vantaux a la forme d’une portion
de courbe.
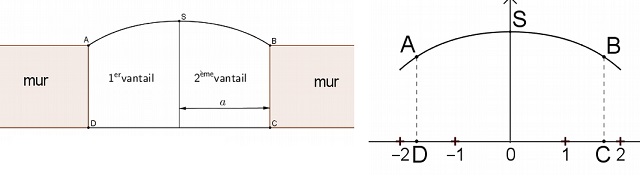
Cette portion de courbe est une partie de la représentation graphique
de la fonction f définie sur
[-2 ; 2] par : f (x) = -b / 8 (ex/b +e-x/b) +9/4
où b est positif.
Le repère est choisi de façon que les points A, B, C et D aient pour
coordonnées respectives
(-a ; f(-a)),(a ; f(a)), (a ; 0) et (-a ; 0) et on note S le sommet de
la courbe de f.
Partie A.
1. Montrer que,
pour tout réel x appartenant à l’intervalle [-2 ; 2], f (-x) = f (x).
Que peut-on
en déduire pour la courbe représentative de la fonction f ?
f(-x) =- b / 8
(e-x/b +ex/b) +9/4= f(x).
La courbe représentative de la fonction est symétrique par rapport à
l'axe des ordonnées.
2. On appelle f ' la fonction
dérivée de la fonction f .Montrer que, pour tout réel x de l’intervalle
[-2 ; 2] : f '(x) = -1/8 (ex/b-e-x/b).
f '(x) = -b /8(1/b ex/b +(-1/b)e-x/b) = -1/8 (ex/b-e-x/b)..
3. Dresser le
tableau de variations de la fonction f sur l’intervalle [-2 ; 2] et en
déduire les
coordonnées du point S en fonction de b.
f '(x) = 0 pour ex/b-e-x/b=0
; ex/b
= e-x/b ; e2x/b =1 soit x
=0.
b étant positif, pour x compris entre -2 et 0, f '(x) est positive et
f(x) est strictement croissante.
Pour x
compris entre 0 et 2, f '(x) est négative et f(x) est strictement
décroissante.
Pour x=0, f(x) = (-b+9) / 4.
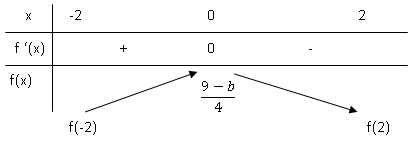
f(-2) =f(2)= -b/8(e-2/b+e2/b)+4/9.
Partie B.
La hauteur du mur est de 1,5 m. On souhaite que le point S soit à 2 m
du sol. On cherche alors les
valeurs de a et b.
1. Justifier que b
= 1.
(9-b) / 4 = 2 ; 9-b = 8 ; b=9-8=1.
2. Montrer que
l’équation f (x) = 1,5 admet une unique solution sur l’intervalle [0
;2] et en déduire
une valeur approchée de a au centième.
-1 / 8 (ex +e-x)
+9/4 =1,5 ; -1 / 8 (ex +e-x)
= -3/4 ; ex +e-x=6
;
e2x-6ex+1=0. On pose X = ex ; X2-6X+1=0
Discriminant D =
36-4=32 ; D½~5,657.
X1 = (6-5,657)/2~0,171 ; X2 =
(6+5,657)/2~5,829 ;
x1 = ln(0,171)~-1,77 , hors de l'intervalle [0 ; 2].
x2 = ln(5,829)~1,76 , compris dans l'intervalle [0
; 2].
3. Dans cette question, on choisit a
=1,8 et b = 1. Le client décide d’automatiser son portail si la
masse d’un vantail excède 60 kg. La densité des planches de bois
utilisées pour la fabrication
des vantaux est égale à 20 kg.m-2. Que décide le client ?
Surface d'un vantail :
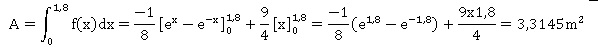
Masse d'un vantail : 20 x3,3145
~66,3 kg, valeur supérieure à 60 kg..
Il décide d'autamatiser le
portail.
Partie C.
On conserve les valeurs a = 1,8
et b= 1.
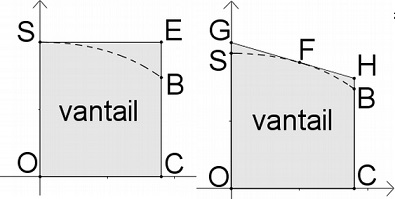
Pour découper les vantaux, le
fabricant prédécoupe des planches. Il a
le choix entre deux formes de
planches prédécoupées : soit un
rectangle OCES, soit un trapèze OCHG
comme dans les schémas ci-dessous. Dans la deuxième méthode, la droite
(GH) est la tangente à la courbe représentative de la fonction f au
point F d’abscisse 1.
La forme 1 est la plus simple,
mais visuellement la forme 2 semble plus
économique.
Évaluer l’économie réalisée en
termes de surface de bois en choisissant
la forme 2 plutôt que la
forme 1.
Aire OCES = 2 x1,8 =3,6 m2 ; pertes de
bois : 3,6 -3,3145
=0,2855 m2.
Equation de la tangente :
f
'(1) = -1/8 (e1-e-1)=
-0,2938.
f(1) = -1 /
8 (e1 +e-1) +9/4=1,864.
y = -0,294 x +b ; 1,864 = -0,2938 +b ; b =2,158.
y = -0,294 x +2,158.
OG = 2,158 ; CH = -0,2938 x1,8 +2,158 ~ 1,63.
Aire du trapèze : 1,8 x(2,158 +1,63) / 2 =3,408 m2 ; perte :
3,408-3,3145 = 0,0935 m2.
Economie de bois : 0,2855 -0,0935 = 0,192
m2.
|
|
|
Centres
étrangers.
La pharmacocinétique étudie l'évolution d'un médicament après son
administration dans l'organisme, en mesurant sa concentration
plasmatique.
A. Administration par voie
intraveineuse.
On note f(t) la concentration plasmatique ( en µg /L) du médicament ,
au bout de t heures après l'administration. le modèle mathématique est
f(t) = 20 e-0,1t avec t appartenant à [0 ; +oo[.
f(0) = 20 µg /L.
1. La demi-vie du
médicament est la durée en heure après laquelle la concentration
plasmatique du médicament est égale à la moitié de la concentration
initiale. Déterminer cette demi-vie t½.
10 = 20 e-0,1t½ ; ln(0,5) = -0,1 t½ ; t½
=10 ln 2 heures.
2. On estime que le
médicament est éliminé dès que sa concentration est inférieure à
0,2 µg / L.
Déterminer le temps à partir duquel le médicament est éliminé.
0,2 = 20 exp(-0,1t) ; ln 0,01 = -0,1 t ; t = -10 ln(0,01)~46,1 heures.
3. On appelle ASC (
ou aire sous la courbe ) le nombre suivant. Vérifier que l'ASC est égal
à 200 µg /L.h
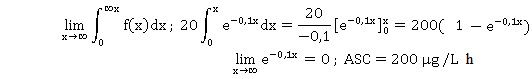
B. Administration par voie
orale.
On note g(t) la concentration plasmatique du médicament ( µg / L) au
bout de t heures après ingestion par voie orale. Le modèle mathématique
est g(t) = 20 (e-0,1t -e-t) avec t appartenant à
[0 ; +oo[. Dans ce cas g(0) = 0.
1. Démontrer que
pour tout t de cet intervalle, g'(t) = 20 e-t(1-0,1e0,9t).
g'(t) = 20 (-0,1 e-0,1t +e-t) =20
(-0,1 e(0,9-1)t +e-t) =20
(-0,1 e0,9t
e-t +e-t) =20
e-t(1-0,1e0,9t).
2. Etudier les
variations de la fonction g(t) sur cet intervalle. En déduire la durée
après laquelle la concentration est maximale ( à la minute près ).
20 e-t est toujours positif.
g'(x) <0 si 0,1e0,9t
>1 soit t > ln(10) / 0,9 = 2,558 heures ou 2 h
34 min.
g(x) est strictement décroissante sur [ 2,558 ; +oo[
g'(x) >0 si 0,1e0,9t <1 soit t >
ln(10) / 0,9 = 2,558 heures.
g(x) est strictement croissante sur [0 ; 2,558[
g't) est nulle si t = ln(10) / 0,9.
g(t) est maximale.
C. Administration répétée
par voie intraveineuse.
On décide d'injecter à intervalles de temps réguliers la même dose de
médicament par voie intraveineuse. l'intervalle de temps entre deux
injections est égal à la demi-vie du médicament.
Chaque nouvelle injection entraîne une hausse de concentration
plasmatique de 20 µg /L.
On note unn. la concentration plasmatique du médicament
immédiatement après la n-ième injection.
Ainsi u1 = 20 et un+1 = 0,5 un +20.
1. Démontrer par
récurrence que, pour tout entier n >1 :
un = 40 -40x0,5n.
Initialisation
: u1 = 20 ; la propriété est vraie au rang 1.
Hérédité :
la propriété est supposée vraie au rang p : up
= 40 -40x0,5p.
up+1 =
0,5 up +20 = 20-40x0,5p x0,5+20
up+1 =40
-40 0,5p+1 . la propriété est vraie
au rang p+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire.
La propriété est vraie pour tout n >1.
2. Déterminer la
limite de la suite (un) quand n tend vers l'infini.
-1 < 0,5 <1 ; par suite 0,5n tend vers zéro
quand n tend vers l'infini.
La suite tend vers 40 quand n tend vers l'infini.
3. On considère que
l'équilibre est atteint dès que la concentration plasmatique dépasse 38
µg /L. Déterminer le nombre minimal d'injections nécessaire pour
atteindre cet équilibre.
un
= 40 -40x0,5n =38 ; 2 / 40 = 0,5n ; n = ln(0,05)
/ ln(0,5 )~ 4,3.
Après 5 injections, l'équilibre est atteint.
|
|
|
|
Polynésie.
On
s'intéresse à la chute d'une goutte d'eau qui se détache d'un nuage
sans vitesse initiale.
Un modèle simplifié donne la vitesse verticale de chute ( en m /s) en
fonction du temps.
v(t) = 9,81 m / k (1-exp(-kt /m)).
m : masse de la goutte en mg ; k >0 coefficient lié au frottement de
l'air.
A. Cas général.
1. Déterminer les
variations de la vitesse de la goutte.
v '(t) = 9,81 m /k (-k /m)(-exp(-kt /m)) =9,81exp(-kt /m).
La dérivée étant strictement positive sur [0 ; +oo[, la vitesse est
strictement croissante.
2. La goutte
ralentit-elle au cours de sa chute ?
Non, la vitesse initiale est nulle ; la vitesse limite vaut 9,81 m /k
et v(t) est strictement croissante.
3. Montrer que la
vitesse limite de chute est Vlim = 9,81 m / k.
Quand t tend vers l'infini, kt / m étant positif, le terme en
exponentielle tend vers zéro.
Par suite la vitesse tend vers 9,81 m / k.
4. Un scientifique
affirme qu'au bout d'une durée de chute égale à 5m /k, la vitesse de la
goutte dépasse 99 % de sa vitesse limite. Cette affirmation est-elle
correcte ?
exp(-k / m x 5m / k) = exp(--5) ; v(5m /k) = 9,81 m /k (1-e-5)
~0,993 x9,81 m /k ~0,993 Vlimite.
L'affirmation est correcte.
B. On prend m =6 et
k =3,9.
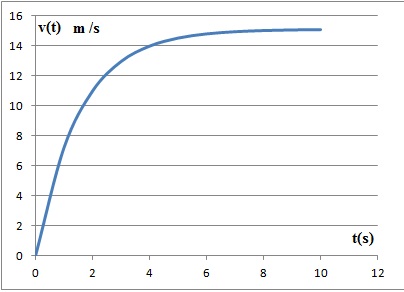
A un instant donné v(t) = 15 m /s.
1. Depuis combien
de temps la goutte s'est-elle détachée de son nuage ? Arrondir le
résultat au dixième de seconde.
v(t)
= 9,81 x 6 / 3,9 (1-exp(-3,9 t / 6)) =15,092 (1-exp(-0,65 t)) = 15 ;
.1-exp(-0,65 t) = 15 / 15,092
~0,99389 ; exp(-0,65 t)
=0,006116.
-0,65 t = ln(0,006116) = -5,0968 ; t ~7,84 s ; t ~7,8 s.
2.
En déduire la vitesse moyenne de cette goutte entre le moment où elle
s'est détachée du nuage et l'instant où est mesurée sa vitesse.
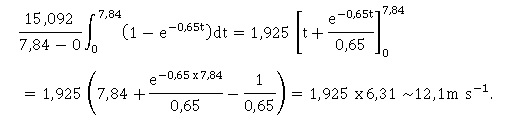
|
Antilles.
Soient f et g les fonctions définies sur l’ensemble R des nombres réels
par
f(x) = ex et g(x)= e−x.
On note Cf la courbe représentative de la fonction f et Cg
celle de la fonction g dans un
repère orthonormé du plan.
Pour tout réel a, on note M le point de Cf d’abscisse a et N
le point de Cg d’abscisse a.
La tangente en M à Cf coupe l’axe des abscisses en P, la
tangente en N à Cg coupe l’axe des
abscisses en Q.
À l’aide d’un logiciel de géométrie dynamique, on a représenté la
situation pour différentes
valeurs de a et on a relevé dans un tableur la longueur du segment [PQ]
pour chacune de ces
valeurs de a.
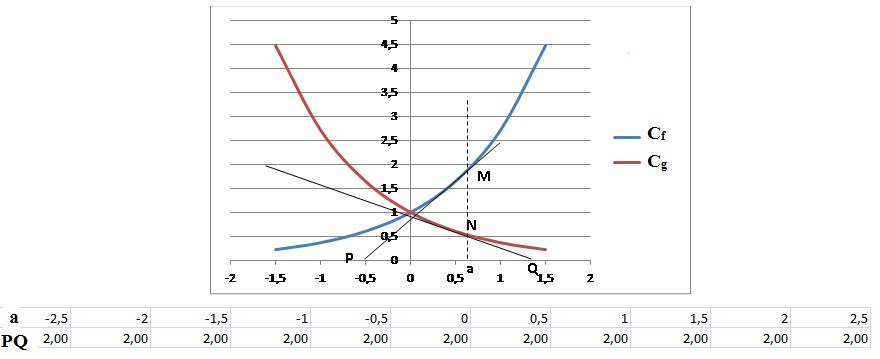
1. Démontrer que la
tangente en M à Cf est perpendiculaire à la tangente en N à Cg.
Coefficient directeur de la tangente à Cf en M d'abscisse a
: f '(a) = ea.
Cette tangente passe en M ( a ; ea).
Equation de cette tangente : y = eax +b ; ea = a ea
+b ; b = ea(1-a) ; y = eax
+ea(1-a)
Coefficient directeur de la
tangente à Cg en N d'abscisse a : g '(a) = -ea.
Cette tangente passe en N ( a ; e-a).
Equation de cette tangente : y = -e-ax +b' ; e-a
= -a e-a +b' ; b' = e-a(1+a) ; y = -e-ax +e-a(1+a).

2.a.
Que peut-on conjecturer pour la longueur PQ ?
PQ = 2 = constante.
b. Démontrer cette
conjecture
yP=0 ; xP = a-1 ; yQ=0 ; xQ
= a+1 ;
PQ = |xQ -xP |= |a+1-(a-1)| =2.
Métropole.
Partie A.
On considère la fonction h
définie sur l’intervalle 0;+∞ par :h(x)= x e-x.
1. Déterminer la
limite de la fonction h en +∞.
Par croissance comparée, la
limite de ex /x, quand x tend
vers l'infini, est égale plus l'infini.
Donc la limite
de 1 / (ex /x), quand x tend vers l'infini, est égale à zéro.
Or h(x) = x / ex = 1 /(ex/x); par suite la limite
de h(x) en plus l'infini est égale à zéro.
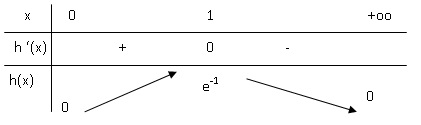
2. Étudier
les variations de la fonction h sur l’intervalle 0;+∞ et dresser son
tableau de variations.
Calculer la dérivée h' en
posant u = x et v = e-x; u' = 1 ;
v' = -e-x.
h'(x) = u'v +v'u = e-x -xe-x=e-x(1-x).
e-x est
toujours positif. Le signe de h'(x) est celui de
(1-x).
Si x appartient à [0 ; 1],
h'(x) est strictement positive et h(x) est
strictement croissante.
Si x
appartient à ]1 ; +oo [, h'(x) est strictement négative et h(x) est
strictement décroissante.
Si x =1, h'(x) est nulle
est h(x) présente un
maximum h(1) = 1/e.
3. L’objectif de
cette question est de déterminer une primitive de la fonction h.
a. Vérifier que
pour tout nombre réel x appartenant à l’intervalle 0;+∞ , on a :
h(x) =e-x -h'(x).
h(x) = xe-x ; h'(x) = e-x -xe-x ;
ajouter : h(x) +
h'(x) = e-x soit h(x) = e-x-h'(x).
b. Déterminer une
primitive sur l’intervalle 0;+∞ de la fonction e-x.
-e-x.
c. Déduire
des deux questions précédentes une primitive de la fonction h sur
l’intervalle 0;+∞ .
H(x) = -e-x -h(x)
= -e-x - xe-x =-
e-x(x+1).
Partie B
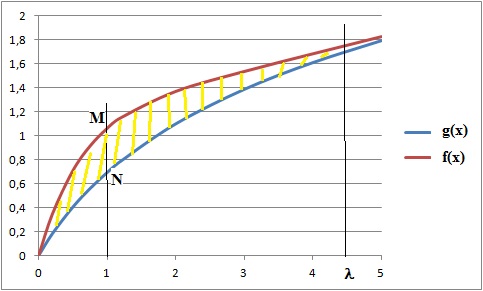
On définit les fonctions f et g sur l’intervalle 0;+∞ par :
f(x) = xe-x+ln(x +1) ; g(x) = ln(x+1).
On note Cf et Cg les représentations graphiques
respectives des fonctions f et g dans un repère orthonormé.
1. Pour un nombre réel x appartenant à l’intervalle 0;+∞ , on appelle M
le point de coordonnées (x ;
f(x)) et N le point de coordonnées (x ; g(x)). M et N sont donc les
points d’abscisse x
appartenant respectivement aux courbes Cf et Cg.
a. Déterminer la valeur de x pour laquelle la distance MN est
maximale et donner cette distance
maximale.
MN =| g(x) - f(x) |= |ln(x+1) - xe-x-ln(x +1)| =
|-xe-x|.
xe-x étant positif, MN = x
e-x.
MN = h(x) ; MN est maximal pour x = 1 et vaut MNmax = e-1.
b. Placer sur le graphique les
points M et N correspondant à la valeur maximale de MN.
Asie.
Un
protocole de traitement d’une maladie, chez l’enfant, comporte une
perfusion longue durée d’un médicament adapté. La concentration dans le
sang du médicament au cours du temps est modélisée par la fonction C
définie sur l’intervalle [0;+oo[ par :
C(t) = d /a [1-exp(-at / 80)]
C désigne la concentration du
médicament dans le sang, exprimée en
micromole par litre,
t le temps écoulé depuis le
début de la perfusion, exprimé en heure,
d le débit de la perfusion,
exprimé en micromole par heure,
a un paramètre réel strictement
positif, appelé clairance, exprimé en
litre par heure.
Le paramètre a est spécifique à
chaque patient.
En médecine, on appelle «
plateau » la limite en +oo de la fonction C.
Partie A : étude
d’un cas particulier.
La clairance a d’un certain
patient vaut 7, et on choisit un débit d
égal à 84.
Dans cette partie, la fonction
C est donc définie sur [0;+oo[ par :
C(t) = 12 [1-exp(-7t /80)}.
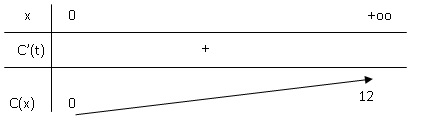
1. Étudier le sens
de variation de la fonction C sur [0;+oo[ .
Calcul de la dérivée C'(t) = 12
x(7 /80 exp(-7t /80) = 21 /20 exp(-tt
/80).
C'(t) est positive sur [0;+oo[
; C(t) est strictement croissante.
2. Pour être
efficace, le plateau doit être égal à 15. Le traitement de ce patient
est-il efficace ?
Le plateau est égal à 12, le traitement n'est
pas efficace.
Partie B. Etude de
fonctions.
1. Soit f la
fonction définie sur ]0 ;+oo[ par :
f(x) = 105 / x [1-exp(-3x /40)]
Démontrer que, pour tout réel x de ]0 ;+oo[ , f '(x) =105 g(x) / x2.
où g est la fonction définie sur [0;+oo[ par :
g(x) = 3x /40 exp(-3x /40) +exp(-3x /40) -1.
On pose u = [1-exp(-3x /40)] et v = x
; u' = 3/40 exp(-3x /40) et v' = 1.
f '(x) = (u'v-v'u) / v2 =105 [
3x/40 exp(-3x /40)- 1+exp(-3x
/40)] /x2.
2. On
donne le tableau de variation de la fonction g. En déduire le sens de
variation de la fonction f.
On ne demande pas les limites de la fonction f.
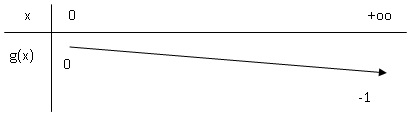
g(x) est négative sur ]0 ;+oo[ et 105 /x2 est
positif.
Donc f '(x) est négative et par suite f (x) est strictement
décroissante.
3. Montrer que
l’équation f (x) = 5,9 admet une unique solution sur l’intervalle
[1;80].
En
déduire que cette équation admet une unique solution sur l’intervalle
]0 ;+oo[ .
Donner une valeur approchée de cette solution au dixième près.
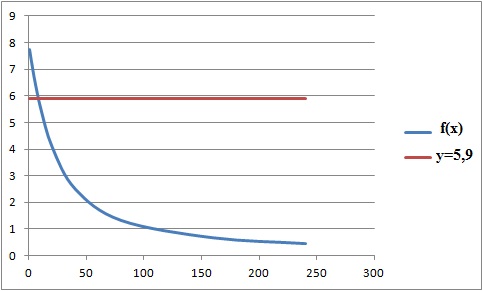
f(1) = 105(1-exp(-3/40))~7,58 >5,9 ; f(80)
= 105 /80 (1-exp(-3*2))~1,31 <5,9.
De plus la fonction f(x) est strictement décroissante sur [1 ; 80].
D'après
le théorème des valeurs intermédiaires, l’équation f (x) = 5,9 admet
une unique solution sur l’intervalle
[1;80].

Partie C :
détermination d’un traitement adéquat
Le but de cette partie est de déterminer, pour un patient donné, la
valeur du débit de la perfusion qui permette au traitement d’être
efficace, c’est-à-dire au plateau d’être égal à 15.
Au préalable, il faut pouvoir déterminer la clairance a de ce patient.
À cette fin, on règle provisoirement le débit d à 105, avant de
calculer le débit qui rende le traitement efficace.
On rappelle que la fonction C est définie sur l’intervalle [0;+oo[ par : C(t) = d /a [1-exp(-at /
80)]
1. On cherche à
déterminer la clairance a d’un patient. Le débit est provisoirement
réglé à 105.
a) Exprimer en
fonction de a la concentration du médicament 6 heures après le début de
la perfusion.
C(6) = d /a [1-exp(-6a / 80)] =d /a
[1-exp(-3a / 40)] = 105 /a [1-exp(-3a / 40)]
b)
Au bout de 6 heures, des analyses permettent de connaître la
concentration du médicament dans le sang ; elle est égale à 5,9
micromole par litre. Déterminer une valeur approchée, au dixième de
litre par heure, de la clairance de ce patient.
a = 8,1 micromoles
par litre.
2. Déterminer la valeur du débit d
de la perfusion garantissant l’efficacité du traitement.
15 = d / 8,1 ; d = 15 x8,1 = 121,5 micromoles par heure.
Nlle
Calédonie.
On considère la fonction f
définie sur ]0 ; +∞[ par
f (x) =(ln x)2 / x.
On note C la courbe
représentative de f dans un repère orthonormé.
1. Déterminer la
limite en 0 de la fonction f et interpréter graphiquement le résultat.
Quand
x tend vers
zéro, (lnx)2 tend vers
l'infini et 1 /x tend vers
l'infini.
Par produit des limites, f(x)
tend vers l'infini.
L'axe des ordonnées est
asymptote à la courbe C.
2. a. Démontrer
que, pour tout x appartenant à ]0 ; +∞[,
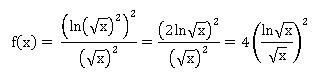
.
b. En déduire que
l’axe des abscisses est une asymptote à la courbe représentative de la
fonction f au voisinage de +∞.
On pose t = x½ ; ln (t ) /
t tend vers zéro si t tend vers
plus l'infini.
L'axe des
abscisses est une asymptote à la courbe C au voisinage de +∞.
3. On admet que f
est dérivable sur ]0 ; +∞[ et on note f ′ sa fonction dérivée.
a. Démontrer que,
pour tout x appartenant à ]0 ; +∞[,
f ′(x) =ln(x) (2−ln(x)) /x2 .
On pose u =( ln x)2 et v = x ;
u' = 2 ln(x) / x ; v' = 1.
(u'v-v'u) / v2 = (2
ln(x)-(ln x)2)/x2=ln
x ( 2-ln x) / x2.
b. Étudier le signe
de f ′(x) selon les valeurs du nombre réel x strictement positif.
Le signe de f '(x) est celui de
ln x .(2-ln x).
c. Calculer f (1)
et f (e2).
On obtient alors le tableau de
variations ci-dessous.
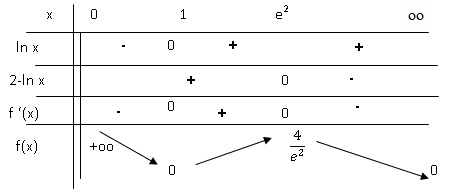
4. Démontrer que
l’équation f (x) = 1 admet une unique solution a sur ]0 ; +∞[ et donner un
encadrement de a
d’amplitude 10−2.
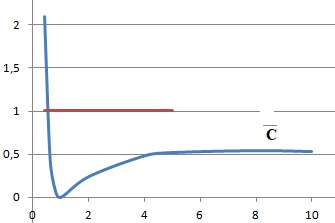
f(x) est inférieure à 1
sur [1 +oo[ et ; f(x) est strictement
décroissante sur ]0 ; 1[.
f(0,001) tend vers l'infini et
f(1) = 0.
D'après le corrolaire du
théorème des valeurs intermédaires, f(x)=1
admet une seule solution sur ]0 ; + oo[.
f(0,49) ~1,038 ; f (0,50) ~0,96
; 0,49 < a
< 0,50.
Amérique du Sud
La chocolaterie Delmas décide de commercialiser de nouvelles
confiseries : des palets au chocolat en forme de goutte d’eau.
Pour cela, elle doit fabriquer des moules sur mesure qui doivent
répondre à la contrainte suivante : pour que cette gamme de bonbons
soit rentable, la chocolaterie doit pouvoir en fabriquer au moins 80
avec 1 litre de pâte liquide au chocolat.
Partie A :
modélisation par une jonction
Le demi contour de la face supérieure du palet sera modélisé par une
portion de la courbe de la fonction f définie sur ]0 ; +∞[ par :
f (x) =(x2 −2x −2−3ln x) / x.
La représentation graphique de la fonction f est donnée ci-dessous.
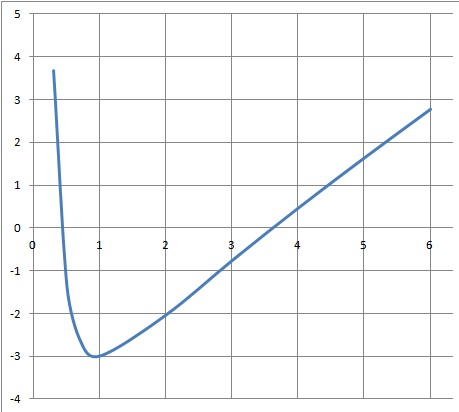
Le repère est orthogonal d’unité 2 cm en abscisses et 1 cm en ordonnées.
1. Soit ϕ la
fonction définie sur ]0 ; +∞[ par :
ϕ(x) = x2 −1+3lnx.
a. Calculer ϕ(1) et
la limite de ϕ en 0.
F(1) =
12-1+3ln(1) = 0.
Quand x tend vers zéro :
x2-1 tend vers -1 et ln(x) tend vers moins l'infini. F(x) tend donc vers moins
l'infini.
b. Étudier les
variations de ϕ sur ]0 ; +∞[.
En déduire le signe de ϕ(x) selon les valeurs de x.
La dérivée 2x +3 / x est positive sur ]0
; +∞[.
F(x)
est strictement croissante sur ]0
; +∞[.
F(x) est négative sur ]0 ;
1[, nulle pour x=1 et positive sur ]1 ; +oo[.
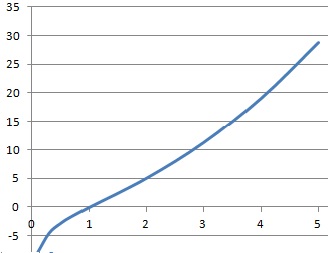
2. a. Calculer les limites de f aux
bornes de son ensemble de définition.
f (x) =x −2
−(2+3ln (x)) / x.
Quand x tend vers
zéro : x-2 tend vers -2 ; (2+3ln
(x)) / x tend vers moins l'infini et
-(2+3ln
(x)) / x tend vers plus l'infini.
Par suite f(x) tend vers plus l'infini.
Quand x tend vers
plus l'infini : x-2 tend
vers plus l'infini ; (2+3ln
(x)) / x tend
vers zéro.
Par suite f(x) tend vers
plus
l'infini.
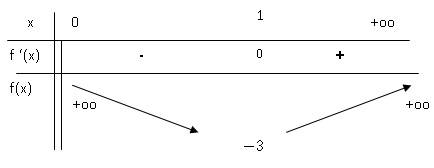
b. Montrer que sur
]0 ; +∞[ : f ′(x) = ϕ(x) / x2 .
En déduire le tableau de variation de f .
On pose u =x2
−2x −2−3ln x et v = x.
u' = 2x-2-3 / x = (2x2-2x-3) / x et v' = 1.
Dérivée d'un quotient : (u'v -v'u) / v2 =[ (2x2-2x-3)-(x2
−2x −2−3ln x) ] / x2=(x2-1+3ln x) / x2=F(x) / x2.
c.
Prouver que l’équation f (x) = 0 admet une unique solution α sur ]0; 1].
Déterminer à la calculatrice une valeur approchée de α à 10−2
près.
Sur ]0 ; 1], f(x) est strictement décroissante.
De plus f(1) est négatif et f(0,1) est positif.
D'après le corolaire du théorème des valeurs intermédiaires, f(x) = 0
admet une unique solution sur ]0 ; 1].
Solution de f(x)=0, x ~ 0,41.
On admettra que l’équation f (x) = 0 a également une unique solution β
sur [1 ; +∞[ avec β ≈ 3,61 à 10−2 près.
d. Soit F la
fonction définie sur ]0 ; +∞[ par :
F(x) =0,5 x2 -2x -2ln(x) -1,5( ln(x))2.
Montrer que F est une primitive de f sur ]0 ; +∞[.
Dériver F : F ' = 0,5 *2 x-2-2 / x-1,5*2 ln(x) / x = x-2-2 / x -3ln(x)
/ x = (x2-2x-2-3ln(x) ) / x = f(x).
Partie B :
résolution du problème.
Dans cette partie, les calculs seront effectués avec les valeurs
approchées à 10−2 près de α et β de la partie A.
Pour obtenir la forme de la goutte, on considère la courbe
représentative C de la fonction f restreinte à l’intervalle [α ; β]
ainsi que son symétrique C′ par rapport à l’axe des abscisses. Les deux
courbes C et C′ délimitent la face supérieure du palet. Pour des raisons
esthétiques, le chocolatier aimerait que ses palets aient une épaisseur
de 0,5 cm.
Dans ces conditions, la contrainte de rentabilité serait-elle respectée
?
Aire du palet : 2 | F(ß)-F(a)
|.
F(3,61) ~0,5*3,612-2*3,61-2 ln(3,61)-1,5*(ln(3,61))2
~2 (5,743-0,142) ~11,2 unités d'aire soit 11,2 x2 =22,4 cm2.
Volume du palet : 22,4 x0,5 = 11,2 cm3.
Volume de 80 palets : 896 cm3 = 0,896 L. La contrainte de
rentabilité est respectée.
|
|