Mathématiques,
géométrie, cube, , bac S 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Liban
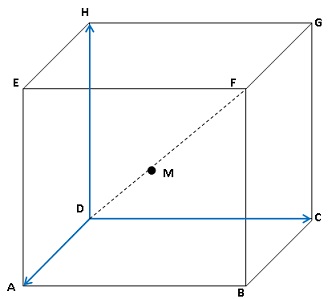
On
considère un cube ABCDEFGH dont la représentation en perspective
cavalière est donnée ci-dessous. Les arêtes sont de longueur 1.
L’espace est rapporté au repère
orthonormé.
Partie A.
1. Montrer que le
vecteur DF est normal au plan (EBG).
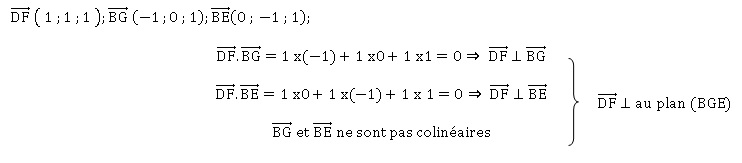
2. Déterminer une
équation cartésienne du plan (EBG).
x+y+z+d=0.
Le point E(1 ; 0 ; 1)
appartient à ce plan : 1+0+1+d=0 soit d = -2.
x+y+z-2=0.
3. En déduire les
coordonnées du point I intersection de la droite (DF) et du plan (EBG).
Equation paramétrique de la
droite (DF) :
x = t +xD = t ; y =t+yD = t ; z = t
+zD
= t.
I appartient à la droite
(DF) et au plan(EBG) : t+t+t-2 = 0 soit
t = 2/3.
I(2/3 ; 2/3
; 2/3).
On démontrerait de la même
manière que le point J intersection de la
droite (DF) et du plan
(AHC) a pour coordonnées J(1/3
; 1/3 ; 1/3).
.Partie B.
À tout réel x de l’intervalle
[0 ; 1], on associe le point M du segment
[DF] tel que
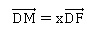
On s’intéresse à
l’évolution de la mesure q
en radian de l’angle EMB
lorsque le point M parcourt le
segment [DF]. On a 0 < q
< p.
1. Que vaut q
si le point M est confondu
avec le point D ? avec le point F ?
M confondu avec D : le triangle
EDB est équilatéral : les trois côtés
sont égaux à la diagonale d'un carré de côté 1. q = p/3.
M confondu avec F : q = p/2.
2.a) Justifier que
les coordonnées du point M sont (x ;x ;x).
Equation paramétrique de la
droite (DF) : x=t ; y = t ; z = t.
M appartient à cette droite : xM = yM =zM
= t.
b) Montrer que cos(q) =(3x2-4x+1) / (3x2-4x+2)
.
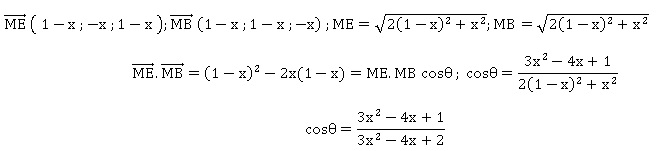
3. On a construit
ci-dessous le tableau de variations de la fonction f(x) =(3x2-4x+1) / (3x2-4x+2).
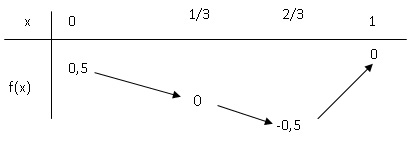
Pour quelles
positions du point M sur le
segment [DF] :
a) le triangle MEB
est-il rectangle en M ?
cosq = 0 ; 3x2-4x+1=0
; D = 16-12=4 ; x1
=(4+2)/2=1 ; M confondu avec F.
x2=(4-2)/6=1/3. M est confondu avec J.
b) l’angle q
est-il maximal ?
q
est maximal quand cos q
est minimal ; f(x) est
minimal pour x = 2/3 ; M est
en I.
|
| .
. |
....
.....
|
Amérique du Nord.
Un particulier s’intéresse à l’ombre
portée sur sa future véranda par
le toit de sa maison quand le soleil est au zénith. Cette véranda est
schématisée ci-dessous en perspective cavalière dans un repère
orthonormé
. Le toit de la véranda
est constitué de deux faces triangulaires SEF
et SFG.
• Les plans (SOA) et
(SOC) sont perpendiculaires.
• Les plans (SOC) et (E
AB) sont parallèles, de même que les plans
(SOA) et (GCB).
• Les arêtes [UV ] et
[EF] des toits sont parallèles.
Le point K appartient au
segment [SE], le plan (UV K) sépare la véranda
en deux zones, l’une éclairée et l’autre ombragée. Le plan (UV K) coupe
la véranda selon la ligne polygonale KMNP qui est la limite
ombre-soleil.
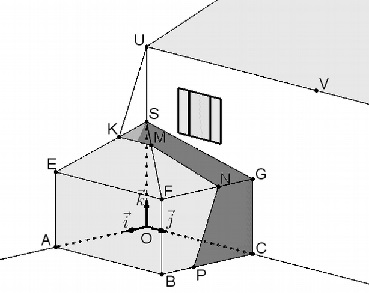
1. Sans calcul,
justifier que :
a) le segment [KM]
est parallèle au segment [UV ] ;
La droite (UV) du plan
(UVK) est parallèle à la droite (EF) du plan
(SEF).
Les plans (UVK) et (SEF)
se coupent suivant la droite (KM).
D'après le théorème du
toit, les droites(KM), (UV) et (EF) sont
parallèles.
b) le segment [NP]
est parallèle au segment [UK].
Les plans (SEA) et (GCB)
sont parallèles.
La droite (UK) est
l'intersection des plans (SEA) et (GCB).
En conséquence, le plan
(UKV) coupe le plan (GCB) suivant une droite
parallèle à (UK).
Par suite (UK) est
parallèle à (NP).
2. Dans la suite
de l’exercice, on se place dans le repère orthonormé.
. Les coordonnées des
différents points sont les suivantes : A(4 ;0 ;
0), B(4 ;5 ; 0), C(0 ;5 ; 0), E(4 ;0 ; 2, 5),
F(4 ;5 ; 2, 5), G(0 ;5 ;
2, 5), S(0 ;0 ; 3, 5),U(0 ;0 ;6) et V (0 ;8 ;
6).
On souhaite déterminer de
façon exacte la section des faces visibles de
la véranda par le plan
(UV K) qui sépare les
zones ombragée et ensoleillée.
a) Au moment le
plus ensoleillé, le point K a pour abscisse 1, 2. Vérifier que les
coordonnées du point K sont (1,2 ;0 ; 3, 2).
Coordonnées des points S
et E : S(0 ;0 ; 3, 5) et E(4 ;0 ; 2, 5).
Coordonnées du vecteur SE
: (4-0 ; 0-0 ; 2,5-3,5) soit (4 ; 0 ; -1).
Représentation
paramétrique de la droite (SE) :
x=4t +xS
= 4t ; y =0 t+yS = 0 ; z=-t+zS
=-t+3,5 avec t réel.
K apparteint à cette
droite et l'abscisse de K est égale à 1,2 : 1,2 =
4t soit t = 1,2 /4 = 0,3.
yK
=0 ; zK = -0,3 +3,5 = 3,2.
K(1,2 ; 0 ; 3,2).
b) Montrer que le
vecteur n de coordonnées (7 ;0 ;3) est un vecteur normal au plan (UV K)
et en déduire une équation cartésienne du plan (UV K).
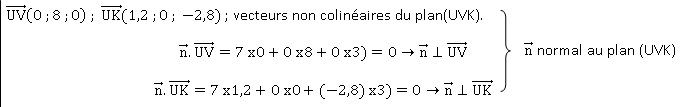
Equation cartésienne de
ce plan : 7x+3z+d=0.
U(0 ; 0; 6) appartient à
ce plan : 7 x0 +3 x6 +d = 0 ; d = -18.
7x+3z-18=0.
c) Déterminer les
coordonnées du point N intersection du plan (UV K) avec la droite (FG).
N appartient au plan
(UVK) : 7 xN +3zN-18 = 0.
N apparteint à la droite
(FG) de vecteur directeur (xG-xF
; yG-yF ; zG-zF) soit (-4 ;
0 ; 0).
Représentation
paramétrique de cette droite : x = -4t +xG
=
-4t ; y =yG =5 ; z = zG
=2,5.
Par suite xN =
-4t ; yN = 5 ; zN =
2,5.
7 xN
+3zN-18 = 0 ; -28t +3 x2,5= 18 ; t = -21 /
56 ; N(
-1,5 ; 5 ; 2,5).
d) Expliquer
comment construire la ligne polygonale sur le schéma de la véranda.
OA = 4 ; xK
/ 4 = 1,2 / 4 = 0,3. On place le point L du
segment [OA] tel que [OL]=0,3 {OA].
La droite passant par L
et parallèle à (OU) coupe (ES) en K.
On note Q l'intersection
de la droite (UK) avec le segment [OA].
Construire une droite
parallèle àla droite (EF) et passant par K.
Celle-ci coupe le segment [SF) en M.
N(1,5 ; 5 ; 2,5)
appartient au segment (FG] ; GF = 4 ; vecteur GN
= 3 / 8 x vecteur GF.
Tracer [MN].
la droite parallèle à la
droite (UK) passant par N coupe [BC] en P.
On trace les segments
[NP] et {PQ].
3. Afin de
faciliter l’écoulement des eaux de pluie, l’angle du segment [SG] avec
l’horizontale doit être supérieur à 7°. Cette condition est-elle
remplie ?
On
note H, point du segment [OS) tel que le triangle SGH soit rectangle en
H.
SH = 3,5-2,5 = 1 ; HG =
OC = 5.
Tangente de l'angle SGH =
1 / 5 = 0,2 ; l'angle SGH mesure environ
11,3° > ¨7°.
La condition est remplie.
|
|
|
Centres
étrangers.
L'espace
est muni d'un repère
orthonormé. On considère deux droites d1 et d2
définies par leurs représentations paramétriques :
d1 : x=2+t ; y = 3-t ; z =t, avec t réel.
d2 : x = -5+2t' ; y = -1+t' ; z=5, avec t' réel.
On admet que ces droites
sont non coplanaires.
But de l'exercice
: existe-t-il une droite D
qui soit à la fois sécante avec d1 et d2 et
orthogonale à ces deux droites.
1. Vérifier que le
point A(2 ; 3 ; 0) appartient à d1.
xA=2 = 2 +t soit t=0 ; par suite y = 3-0 = 3 = yA
; z = 0 = zA.
2. Donner un
vecteur directeur de chaque droite. Ces droites sont-elles parallèles ?
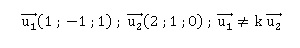
Ces vecteurs n'étant pas colinéaires, ces droites ne sont pas
parallèles.
3. Vérifier que le
vecteur de coordonnées (1 ; -2 ; -3) est orthogonal aux vecteurs
précédents.
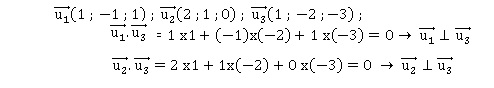
4. Soit P le plan
passant par le point A et dirigé par les vecteurs u1 et u3.
On étudie dans cette question l'intersection de la droite d2
avec ce plan P.
a. Montrer qu'une
équation cartésienne du plan P est 5x+4y-z-22 = 0.
Equation du plan P : ax +by +cz +d = 0.
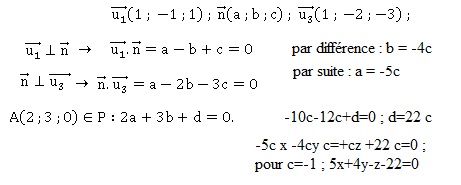
b. Montrer que la
droite d2 coupe le plan P en B(3 ; 3 ; 5).
5(-5+2t') +4(-1+t') -5-22=0 ; 14 t' = 56 ; t' = 4.
Par suite la droite d2 et le plan P se coupent au point de
coordonnées (3 ; 3 ; 5).
5. On consodère la
droite D de
vecteur directeur u3 (1 ; -2 ; -3) et passant par le point B.
a. Donner une représentation paramétrique de cette droite.
x = t" +xB = t"+3 ; y = -2t" +yB = -2t" +3 ; z =
-3t" +zB = -3t" +5 avec t" réel.
b. Les droites d1
et D sont-elles
sécantes ? Justifier.
Si ces droites sont sécantes :
x=2+t =t"+3 soit t = t"+1 ;
y = 3-t=-3-t"-1 = -2t"+3 soit t"=1 et t =2.
z =t =-3t"+5 ; 2 = -3+5 est bien vérifié.
Les droites d1 et
D sont
sécantes au point de coordonnées (4 ; 1 ; 2).
c. Expliquer
pourquoi la droite D
répond au problème.
D'après 3, la droite D
est orthogonales aux droites d1 et d2.
D'après 5b, les droites D et d1 sont
sécantes.
L'intersection de D et d2 est le
point B.
D est sécante avec les
droites d1 et d2 et orthogonale à ces droites.
|
|
|
|
Polynésie.
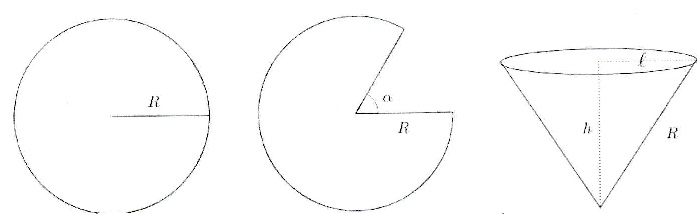
Dans un disque en carton de rayon R
on découpe un secteur angulaire correspondant à un angle a. On supperpose les bords
du disque afin d'obtenir un cône de révolution. On souhaite choisir a afin d'avoir un cône de
volume maximal.
1. On choisit R = 20 cm.
a. Montrer que le volume du cône en
fonction de sa hauteur h est V(h) = p /3 (400-h2)h.
Volume d'un cône : V = 1 / 3 surface de base fois hauteur.
Surface de base : p(R2-h2)
= p(400 -h2).
Par suite V(h) = p /3 (400-h2)h.
b. Justifier qu'il existe une valeur
de h qui rend le volume du cône maximum. Donner cette valeur.
V '(h) = p /3 (400-3h2).
V '(h) = 0 pour h = 20 / 3½.
Si h < 20 / 3½ , la
dérivée V '(h) est positive et V(h) est croissante.
Si h > 20 / 3½
, la dérivée V '(h) est négative et V(h) est décroissante.
Il s'agit donc d'un maximum.
c. Comment découper le disque pour
avoir un volume maximum ? Donner un arrondi de a au degré près.
On note r le rayon de la base du cône ; r = (R2-h2)½
;
l = 2p r = (2p-a)R ; a = 2p (1-r / R).
Le
volume est maximal si h2 = 400 / 3 ; r = (R2-400 /3)½
;
Or R = 20 cm ; r = (202-400 /3)½
= 20 x2½ / 3½~16,33 cm.
a = 2p (1-r / R)~2p (1-16,33 / 20)~0,367 p radian ou 66°.
b. L'angle a dépend-il du rayon R du
disque en carton ?
Non : a = 2p (1-r / R) avec r = (R2-h2)½
et h2=R2/3.
r = (R2-R2/3)½
= (2R2/3)½
=R x(2 / 3)½ ; r / R = (2 / 3)½
;
a = 2p (1- (2 / 3)½).
Exercice 3.
L'objectif est de déterminer
une mesure de l'angle entre deux liaisons carbone-hydrogène dans la
molécule de méthane.
Un tétraèdre régulier est un
polyèdre dont las quatre faces sont des triangles équilatéraux.
1. Justifier que
l'on peut inscrire ce tétraèdre dans un cube ABCDEFGH en positionnant 2
atomes d'hydrogène sur les sommets A et C du cube et les deux autres
atomes d'hydrogène sur deux autres sommets du cube. Représenter la
molécule dans le cube donné.
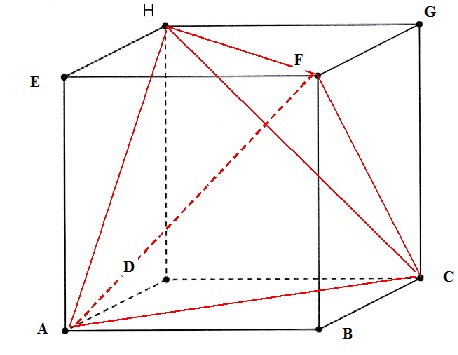
Tous les segments rouges ont
même mesure celle de la diagonale d'un carré.
Les triangles ACH, CHF, AFH et
ACF sont équilatéraux.
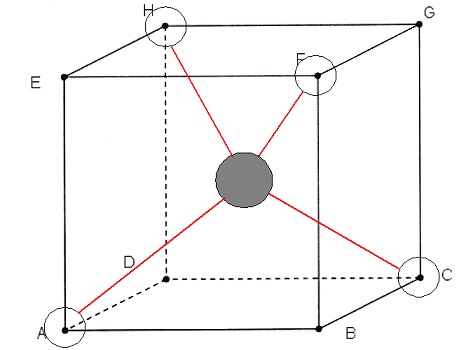
On travaillera dans
le repère indiqué ci-dessous.
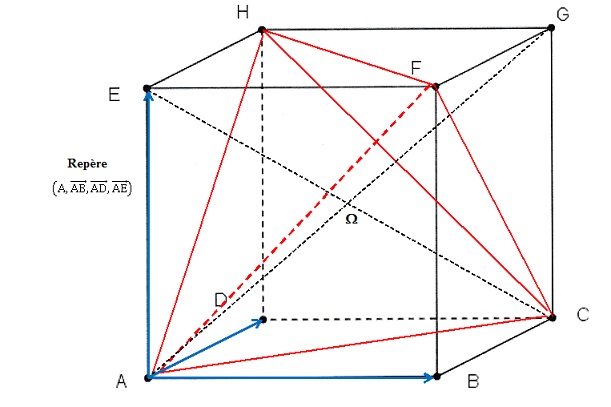
2. Démontrer que l'atome de carbone
est au centre W
du cube.
Toutes les distances carbone-hydrogène sont égales.
Le centre du cube est à égale distance des sommets du cube.
W( 0,5
; 0,5 ; 0,5).
3. Déterminer
l'arrondi au dixième de degré de la mesure de l'angle que forment entre
elles les liaisons carbone-hydrogène.
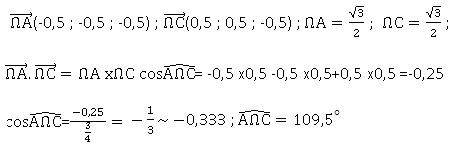
|
Antilles.
On note R l’ensemble des nombres réels.
L'espace est muni d'un repère orthonormé (O, i, j, k).
On considère les points A(−1; 2; 0), B(1; 2; 4) et C(−1; 1; 1).
1.a. Démontrer que
les points A, B et C ne sont pas alignés.
b. Calculer le
produit scalaire suivant.
c. En déduire la
mesure de l’angle BAC , arrondie au degré.
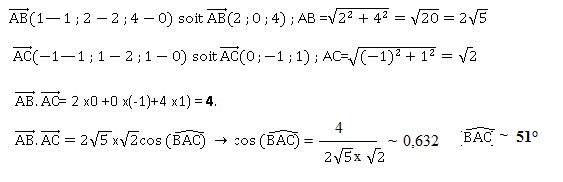
2. Soit n le
vecteur de coordonnées (2 ; -1 ; -1).
a. Démontrer que ce
vecteur est un vecteur normal au plan (ABC).
b. Déterminer une
équation cartésienne du plan (ABC).
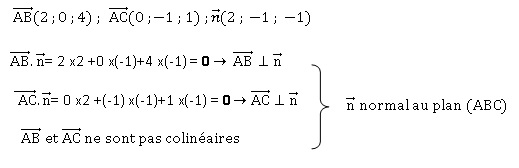
Equation cartsienne du plan (ABC) : 2x -y -z +d =0.
Les coordonnées du point A vérifient cette équation : 2(-1)-2-0+d=0
soit d = 4.
Par
suite : 2x -y -z +4 =0.
3. Soient p1 le plan
d'équation 3x + y − 2z + 3 = 0 et p2 le plan passant par O
et parallèle au plan d'équation x -2z + 6 = 0.
a. Démontrer que le
plan p2 a pour équation x=2z.
L'équation cartésienne du plan p2 est de la forme
x-2z+d=0.
Les coordonnées du point O(0 ; 0 ; 0) vérifient cette équation :
0-2x0+d = 0 soit d =0 ;
par suite : x-2z=0
ou x = 2z.
b. Démontrer que
les plans p1 et p2 sont sécants.
Un vecteur normal au plan p1 a pour coordonnées (3 ; 1 ; -2).
Un
vecteur normal au plan p2 a pour coordonnées (1 ; 0 ; -2).
Ces deux vecteurs ne sont pas colinéaires. Donc les
plans p1 et p2 sont sécants.
c. Soit la droite D dont un système
d'équations paramétriques est
x=2t ; y=-4t-3 ; z=t avec t réel.
Démontrer que D est l’intersection des plans p1 et p2.
Pour tout réel t : 3(2t)+(-4t-3)-2t+3=6t-6t-3+3=0 ; donc D est incluse
dans p1.
Pour
tout réel t : 2t -2t=0 ; donc D
est incluse dans p2.
Ces deux plans étant sécants suivant une droite, cette droite ne peut
être que la droite D.
4. Démontrer que la droite D coupe
le plan (ABC) en un point I dont on déterminera les coordonnées.
Il faut résoudre le système :
x=2t ; y=-4t-3
; z=t et 2x -y
-z +4 =0.
4t-(-4t-3)-t+4=0 ; 7t +7=0 ; t = -1.
Par suite x =-2 ; y =4-3 = 1 ; z = -1.
La droite D et le plan ABC n'ont qu'un seul point commun obtenu pour t
=-1.
Les coordonnées de ce point sont I(-2 ; 1 ; -1).
Métropole.
L’espace
est muni d’un
repère orthonormé (O, i, j, k).
Soit P le plan d’équation cartésienne : 2x −z − 3 = 0.
On note A le point de coordonnées (1 ; a ; a2), où a est un
nombre réel.
1. Justifier que,
quelle que soit la valeur du réel a, le point A n’appartient pas au
plan P.
Si A appartient au plan P, ces coordonnées vérifient l'équation
cartésienne de ce plan.
2-a2-3 =0 ; a2 = -1 ; impossible.
A n'appartient pas au plan P.
2. a. Déterminer
une représentation paramétrique de la droite D (de paramètre noté t)
passant par
le point A et orthogonale au plan P.
Coordonnées d'un vecteur directeur de cette droite : (2 ; 0 ; -1).
Représentation paramétrique de cette droite ;
x = 2t +xA =2t +1.
y = 0 +yA = a ; z = -t +zA = -t +a2.
b. Soit M un point
appartenant à la droite D, associé à la valeur t du paramètre dans la
représentation paramétrique précédente.
Exprimer la distance AM en fonction du réel .
AM2 = (2t+1-1)2 +(a -a)2 +(-t+a2-a2)2.
AM2 =4t2+t2=5t2. AM= 5½|t|.
On note H le point d’intersection du plan P et de la droite D
orthogonale à P et passant par le point A. Le point H est appelé le
projeté orthogonal du point A sur le plan P, et la distance AH est
appelée distance du point A au plan P.
3. Existe-t-il une
valeur de a pour laquelle la distance AH du point A de coordonnées (1
;a ; a2) au
plan P est minimale ? Justifier la réponse.
H appartient à la fois au plan P et à la droite D. Les coordonnées de H
vérifient :
xH = 2t+1 ; yH = a ; zH = -t+a2.
2xH-zH-3 = 0 ; 4t+2+t-a2-3=0 ; 5t =a2
+1 ; t =(a2+1) /5.
D'après la question précédente AH = 5½|t| soit. AH= |a2+1| /5½
=(a2+1) /5½ .
AH est minimum si a = 0 ; AHmini = 5-½.
Amérique
du Sud.
On considère un cube ABCDEFGH.
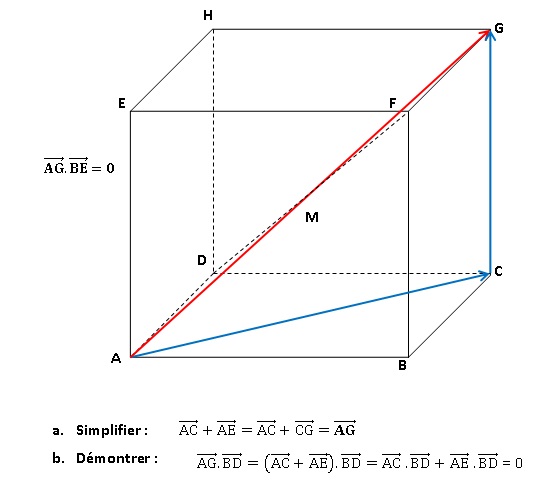
Les diagonales AC et BD du carré sont perpendiculaires.
La base ABCD du cube et la hauteur AEsont perpendiculaires.
c. Démontrer que la
droite (AG) est orthogonale au plan (BDE).
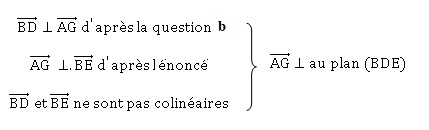
L’espace est muni du repère orthonormé.
a. Démontrer qu’une
équation cartésienne du plan (BDE) est x+y +z−1 =0.

b. Déterminer les
coordonnées du point d’intersection K de la droite (AG) et du plan
(BDE).
Equations paramétriques de la droite (AG) : x = t ; y = t ; z = t avec
t réel.
Les coordonnées de K vérifient à la fois les équations paramétriques de
la droite et celle du plan.
t + t +t -1 = 0 soit t = 1 /3. K( 1/3 ; 1/3 ; 1/3).
c. On admet que
l’aire, en unité d’aire, du triangle BDE est égale à 3½ /2.
Calculer le
volume de la pyramide.
Hauteur de cette pyramide KG=[(1-1/3)2+(1-1/3)2+(1-1/3)2]½=2
/ 3½.
Volume de la pyramide = aire de base x hauteur / 3 = 3½ / 2
x 2 /(3 x3½)=1 / 3 unités de volume.
|
|