Mathématiques :
loi normale, fonction, suite, géométrie.
Bac S Amérique du nord 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice
1.
Partie A.
Dans le cadre de son activité, une entreprise reçoit régulièrement des
demandes de devis. Les
montants de ces devis sont calculés par son secrétariat. Une étude
statistique sur l’année écoulée
conduit à modéliser le montant des devis par une variable aléatoire X
qui suit la loi normale d’espérance µ= 2900 euros et d’écart-type
s=
1250 euros.
1. Si on choisit au
hasard une demande de devis reçue par l’entreprise, quelle est la
probabilité
que le montant du devis soit supérieur à 4000 euros ?
p(X > 4000) =1-P(X
<
4000)=1-0,81057 ~ 0,189.
2. Afin d’améliorer
la rentabilité de son activité, l’entrepreneur décide de ne pas donner
suite à
10% des demandes. Il écarte celles dont le montant de devis est le
moins élevé. Quel doit être
le montant minimum d’un devis demandé pour que celui-ci soit pris en
compte ? Donner ce
montant à l’euro près.
On recherche x tel que P(X < x) = 0,1.
Utiliser la touche " inverse loi normale" de la calculatrice : x = 1298 €.
Partie B.
Ce même entrepreneur décide d’installer un logiciel anti-spam. Ce
logiciel détecte les messages
indésirables appelés spams (messages malveillants, publicités, etc.) et
les déplace dans un fichier
appelé "dossier spam". Le fabricant affirme que 95 % des spams sont
déplacés. De son côté, l’entrepreneur sait que 60% des messages qu’il
reçoit sont des spams. Après installation du logiciel, il constate que
58,6% des messages sont déplacés dans le dossier spam.
Pour un message pris au hasard, on considère les événements suivants :
• D : « le message est déplacé » ;
• S : « le message est un spam».
1. Calculer P(S n
D).
0,60 x0,95 = 0,57.
2. On choisit au
hasard un message qui n’est pas un spam. Montrer que la probabilité
qu’il soit
déplacé est égale à 0,04.
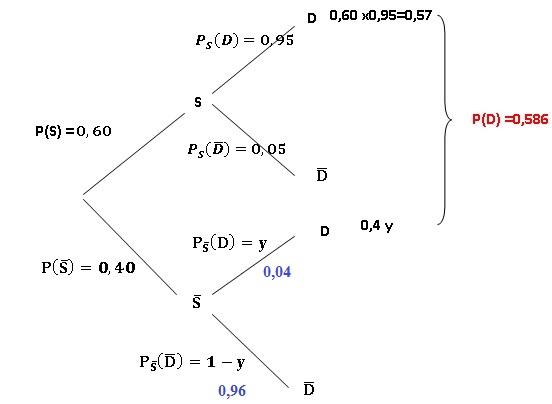
0,586 = 0,57 +0,4 y ; y = (0,586-0,57) / 0,4 = 0,04.
3. On choisit au
hasard un message non déplacé. Quelle est la probabilité que ce message
soit
un spam ?
Probabilité qu'un message soit non déplacé :
0,96 x0,40 + 0,60 x0,05 = 0,414.
Probabilité
qu'un message non déplacé soit un spam : 0,05 x0,60 /0,414=0,072.
4. Pour le logiciel
choisi par l’entreprise, le fabricant estime que 2,7 % des messages
déplacés
vers le dossier spam sont des messages fiables. Afin de tester
l’efficacité du logiciel, le secrétariat
prend la peine de compter le nombre de messages fiables parmi les
messages déplacés.
Il trouve 13 messages fiables parmi les 231 messages déplacés pendant
une semaine.
Ces résultats remettent-ils en cause l’affirmation du fabricant ?
n >0 ; np =231 x0,027 =6,237, supérieur à 5 ; nq = 231
x(1-0,027)=224,7, supérieur à 5.
Intervalle de fluctuation asymptotique au seuil de 95 %:
1,96 x(p q / n) ½ = 1,96 x (0,027 (1-0,027) / 231) ½=0,021.
0,027+0,021 = 0,048 ; 0,027-0,021=0,006.
Intervalle de confiance [0,006 ; 0,048 ].
13 / 231 = 0,056 ; cette valeur n'appartient pas à l'intervalle de
confiance.
L'affirmation du fabricant est remise en cause.
|
| .
. |
....
.....
|
Exercice 2.
Un fabricant doit réaliser un portail en bois plein
sur mesure pour un particulier. L’ouverture du
mur d’enceinte (non encore construit) ne peut excéder 4 mètres de
large. Le portail est constitué
de deux vantaux de largeur a telle que 0 < a < 2.
Dans le modèle choisi, le portail fermé a la forme illustrée par la
figure ci-dessous. Les côtés [AD] et [BC] sont perpendiculaires au
seuil [CD] du portail.
Entre les points A et B, le haut des vantaux a la forme d’une portion
de courbe.
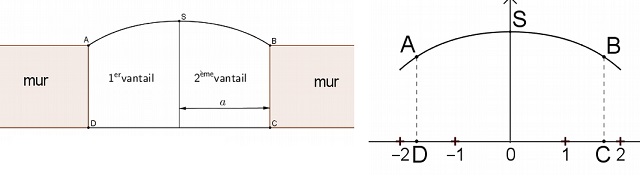
Cette portion de courbe est une partie de la représentation graphique
de la fonction f définie sur
[-2 ; 2] par : f (x) = -b / 8 (ex/b +e-x/b) +9/4
où b est positif.
Le repère est choisi de façon que les points A, B, C et D aient pour
coordonnées respectives
(-a ; f(-a)),(a ; f(a)), (a ; 0) et (-a ; 0) et on note S le sommet de
la courbe de f.
Partie A.
1. Montrer que,
pour tout réel x appartenant à l’intervalle [-2 ; 2], f (-x) = f (x).
Que peut-on
en déduire pour la courbe représentative de la fonction f ?
f(-x) =- b / 8
(e-x/b +ex/b) +9/4= f(x).
La courbe représentative de la fonction est symétrique par rapport à
l'axe des ordonnées.
2. On appelle f ' la fonction
dérivée de la fonction f .Montrer que, pour tout réel x de l’intervalle
[-2 ; 2] : f '(x) = -1/8 (ex/b-e-x/b).
f '(x) = -b /8(1/b ex/b +(-1/b)e-x/b) = -1/8 (ex/b-e-x/b)..
3. Dresser le
tableau de variations de la fonction f sur l’intervalle [-2 ; 2] et en
déduire les
coordonnées du point S en fonction de b.
f '(x) = 0 pour ex/b-e-x/b=0
; ex/b
= e-x/b ; e2x/b =1 soit x
=0.
b étant positif, pour x compris entre -2 et 0, f '(x) est positive et
f(x) est strictement croissante.
Pour x
compris entre 0 et 2, f '(x) est négative et f(x) est strictement
décroissante.
Pour x=0, f(x) = (-b+9) / 4.
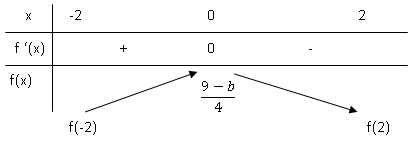
f(-2) =f(2)= -b/8(e-2/b+e2/b)+4/9.
Partie B.
La hauteur du mur est de 1,5 m. On souhaite que le point S soit à 2 m
du sol. On cherche alors les
valeurs de a et b.
1. Justifier que b
= 1.
(9-b) / 4 = 2 ; 9-b = 8 ; b=9-8=1.
2. Montrer que
l’équation f (x) = 1,5 admet une unique solution sur l’intervalle [0
;2] et en déduire
une valeur approchée de a au centième.
-1 / 8 (ex +e-x)
+9/4 =1,5 ; -1 / 8 (ex +e-x)
= -3/4 ; ex +e-x=6
;
e2x-6ex+1=0. On pose X = ex ; X2-6X+1=0
Discriminant D =
36-4=32 ; D½~5,657.
X1 = (6-5,657)/2~0,171 ; X2 =
(6+5,657)/2~5,829 ;
x1 = ln(0,171)~-1,77 , hors de l'intervalle [0 ; 2].
x2 = ln(5,829)~1,76 , compris dans l'intervalle [0
; 2].
3. Dans cette question, on choisit a
=1,8 et b = 1. Le client décide d’automatiser son portail si la
masse d’un vantail excède 60 kg. La densité des planches de bois
utilisées pour la fabrication
des vantaux est égale à 20 kg.m-2. Que décide le client ?
Surface d'un vantail :
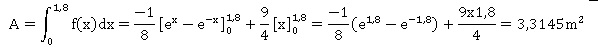
Masse d'un vantail : 20 x3,3145 ~66,3 kg, valeur supérieure à 60 kg..
Il décide d'autamatiser le portail.
Partie C.
On conserve les valeurs a = 1,8 et b= 1.
Pour découper les vantaux, le fabricant prédécoupe des planches. Il a
le choix entre deux formes de
planches prédécoupées : soit un rectangle OCES, soit un trapèze OCHG
comme dans les schémas ci-dessous. Dans la deuxième méthode, la droite
(GH) est la tangente à la courbe représentative de la fonction f au
point F d’abscisse 1.
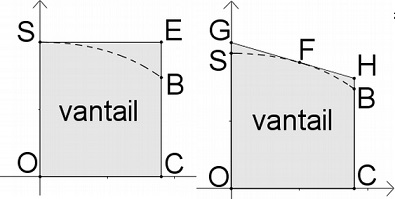
La forme 1 est la plus simple, mais visuellement la forme 2 semble plus
économique.
Évaluer l’économie réalisée en termes de surface de bois en choisissant
la forme 2 plutôt que la
forme 1.
Aire OCES = 2 x1,8 =3,6 m2 ; pertes de bois : 3,6 -3,3145
=0,2855 m2.
Equation de la tangente : f '(1) = -1/8 (e1-e-1)=
-0,2938.
f(1) = -1 /
8 (e1 +e-1) +9/4=1,864.
y = -0,294 x +b ; 1,864 = -0,2938 +b ; b =2,158.
y = -0,294 x +2,158.
OG = 2,158 ; CH = -0,2938 x1,8 +2,158 ~ 1,63.
Aire du trapèze : 1,8 x(2,158 +1,63) / 2 =3,408 m2 ; perte :
3,408-3,3145 = 0,0935 m2.
Economie de bois : 0,2855 -0,0935 = 0,192
m2.
|
|
|
Exercice
3.
Le but de cet exercice est d’étudier les suites de termes positifs dont
le premier terme u0 est strictement supérieur à 1 et
possédant la propriété suivante : pour tout entier naturel n > 0, la
somme des n premiers termes consécutifs est égale au produit des n
premiers termes consécutifs. On admet qu’une telle suite existe et on
la note (un). Elle vérifie donc trois propriétés :
u0 > 1,
pour tout n >
0, un >
0.
pour tout n > 0, sn=u0 +u1+...+un-1= u0 xu1x...xun-1.
1. On choisit u0
= 3. Déterminer u1 et u2.
3+u1=3u1 ; u1=1,5.
3+1,5 +u2=3x1,5 u2
; u2=4,5 /3,5=9 / 7.
2.
a) Vérifier que
pour tout entier n > 0, sn+1 = sn +un
et sn > 1.
sn+1
=u0 +u1+...+un-1+un=sn +un.
sn+1 -sn =un avec un
>0.
sn+1 >sn , la
suite est croissante et le premier terme est strictement supérieur à 1.
b)
En déduire que pour tout entier n >0, un =sn /
(sn -1).
sn+1 =sn xun =sn +un ; un ((sn -1) =sn ; un =sn / (sn
-1).
c)
Montrer que pour tout n >
0 , un > 1.
sn >1, donc sn-1 >0. Par suite sn >sn-1.
Or un =sn / (sn
-1)>0.
3.
À l’aide de l’algorithme suivant, on veut calculer le terme un
pour une valeur de n donnée.
a) Recopier et
compléter la partie traitement de l’algorithme.
Entrée : saisir n ; saisir u.
Traitement : s prend la valeur u.
Pour i allant de 1 à n :
u prend la valeur s /(s-1)
s prend la valeur s+u
Fin pour
Sortie : afficher u.
b) Le tableau
ci-dessous donne des valeurs arrondies au millième de un
pour différentes
valeurs de l’entier n :
n
|
0
|
5
|
10
|
20
|
30
|
40
|
un
|
3
|
1,140
|
1,079
|
1,043
|
1,030
|
1,023
|
Quelle conjecture peut-on faire sur la convergence
de la suite (un) ?
La suite (un) converge vers1.
4.a) Justifier que
pour tout entier n > 0, sn>n.
Initialisation
: s1=u0 >1. La propriété est vraie au rang 1.
Hérédité ;
on supose la propriété vraie au rang p : sp>p.
sp+1 = sp +up avec up >1.
sp +up > p+up
> p+1. La propriété est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire.
Donc
pour tout entier n > 0, sn>n.
b) En
déduire la limite de la suite (sn) puis celle de la suite (un).
Quand n tend vers l'infini, sn tend vers l'infini.
un = sn /
(sn -1) = 1 / (1 -1 /sn).
1
/sn tend vers zéro quand n tend vers l'infini. Donc un
tend vers 1.
|
|
|
|
Exercice
4.
Un particulier s’intéresse à l’ombre portée sur sa future véranda par
le toit de sa maison quand le soleil est au zénith. Cette véranda est
schématisée ci-dessous en perspective cavalière dans un repère
orthonormé
. Le toit de la véranda est constitué de deux faces triangulaires SEF
et SFG.
• Les plans (SOA) et (SOC) sont perpendiculaires.
• Les plans (SOC) et (E AB) sont parallèles, de même que les plans
(SOA) et (GCB).
• Les arêtes [UV ] et [EF] des toits sont parallèles.
Le point K appartient au segment [SE], le plan (UV K) sépare la véranda
en deux zones, l’une éclairée et l’autre ombragée. Le plan (UV K) coupe
la véranda selon la ligne polygonale KMNP qui est la limite
ombre-soleil.
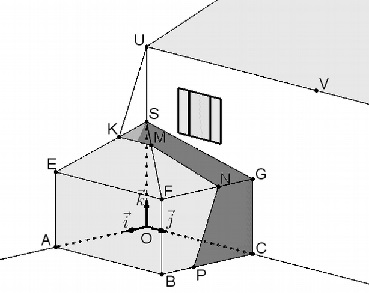
1. Sans calcul,
justifier que :
a) le segment [KM]
est parallèle au segment [UV ] ;
La droite (UV) du plan (UVK) est parallèle à la droite (EF) du plan
(SEF).
Les plans (UVK) et (SEF) se coupent suivant la droite (KM).
D'après le théorème du toit, les droites(KM), (UV) et (EF) sont
parallèles.
b) le segment [NP]
est parallèle au segment [UK].
Les plans (SEA) et (GCB) sont parallèles.
La droite (UK) est l'intersection des plans (SEA) et (GCB).
En conséquence, le plan (UKV) coupe le plan (GCB) suivant une droite
parallèle à (UK).
Par suite (UK) est parallèle à (NP).
2. Dans la suite
de l’exercice, on se place dans le repère orthonormé.
. Les coordonnées des différents points sont les suivantes : A(4 ;0 ;
0), B(4 ;5 ; 0), C(0 ;5 ; 0), E(4 ;0 ; 2, 5),
F(4 ;5 ; 2, 5), G(0 ;5 ; 2, 5), S(0 ;0 ; 3, 5),U(0 ;0 ;6) et V (0 ;8 ;
6).
On souhaite déterminer de façon exacte la section des faces visibles de
la véranda par le plan
(UV K) qui sépare les zones ombragée et ensoleillée.
a) Au moment le
plus ensoleillé, le point K a pour abscisse 1, 2. Vérifier que les
coordonnées du point K sont (1,2 ;0 ; 3, 2).
Coordonnées des points S et E : S(0 ;0 ; 3, 5) et E(4 ;0 ; 2, 5).
Coordonnées du vecteur SE : (4-0 ; 0-0 ; 2,5-3,5) soit (4 ; 0 ; -1).
Représentation paramétrique de la droite (SE) :
x=4t +xS = 4t ; y =0 t+yS = 0 ; z=-t+zS
=-t+3,5 avec t réel.
K apparteint à cette droite et l'abscisse de K est égale à 1,2 : 1,2 =
4t soit t = 1,2 /4 = 0,3.
yK =0 ; zK = -0,3 +3,5 = 3,2.
K(1,2 ; 0 ; 3,2).
b) Montrer que le
vecteur n de coordonnées (7 ;0 ;3) est un vecteur normal au plan (UV K)
et en déduire une équation cartésienne du plan (UV K).
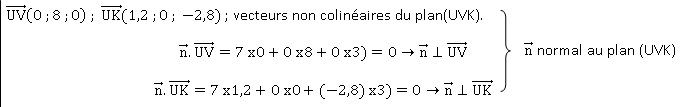
Equation cartésienne de ce plan : 7x+3z+d=0.
U(0 ; 0; 6) appartient à ce plan : 7 x0 +3 x6 +d = 0 ; d = -18.
7x+3z-18=0.
c) Déterminer les
coordonnées du point N intersection du plan (UV K) avec la droite (FG).
N appartient au plan (UVK) : 7 xN +3zN-18 = 0.
N apparteint à la droite (FG) de vecteur directeur (xG-xF
; yG-yF ; zG-zF) soit (-4 ;
0 ; 0).
Représentation paramétrique de cette droite : x = -4t +xG =
-4t ; y =yG =5 ; z = zG =2,5.
Par suite xN = -4t ; yN = 5 ; zN =
2,5.
7 xN +3zN-18 = 0 ; -28t +3 x2,5= 18 ; t = -21 /
56 ; N( -1,5 ; 5 ; 2,5).
d) Expliquer
comment construire la ligne polygonale sur le schéma de la véranda.
OA = 4 ; xK / 4 = 1,2 / 4 = 0,3. On place le point L du
segment [OA] tel que [OL]=0,3 {OA].
La droite passant par L et parallèle à (OU) coupe (ES) en K.
On note Q l'intersection de la droite (UK) avec le segment [OA].
Construire une droite parallèle àla droite (EF) et passant par K.
Celle-ci coupe le segment [SF) en M.
N(1,5 ; 5 ; 2,5) appartient au segment (FG] ; GF = 4 ; vecteur GN
= 3 / 8 x vecteur GF.
Tracer [MN].
la droite parallèle à la droite (UK) passant par N coupe [BC] en P.
On trace les segments [NP] et {PQ].
3. Afin de
faciliter l’écoulement des eaux de pluie, l’angle du segment [SG] avec
l’horizontale doit être supérieur à 7°. Cette condition est-elle
remplie ?
On
note H, point du segment [OS) tel que le triangle SGH soit rectangle en
H.
SH = 3,5-2,5 = 1 ; HG = OC = 5.
Tangente de l'angle SGH = 1 / 5 = 0,2 ; l'angle SGH mesure environ
11,3° > ¨7°.
La condition est remplie.
|
|