Mathématiques,
probabilités, loi normale, loi binomiale, Bac S 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry.
Partie A.
Étude de la durée de vie d’un appareil électroménager
Des études statistiques ont permis de modéliser la durée de vie, en
mois, d’un type de lave-vaisselle par une variable aléatoire X suivant
une loi normale N(μ, s
) de
moyenne μ = 84 et d’écart-type s.
De plus, on a P(X inférieur ou égal à 64) = 0,16.
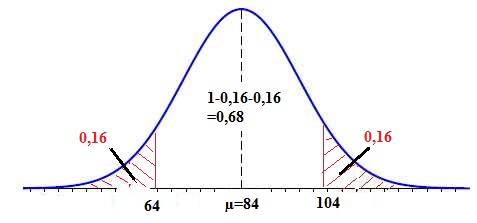
La représentation graphique de la fonction densité de probabilité de X
est donnée ci-dessous.
1. a. En
exploitant le graphique, déterminer P(64<= X <=104).
b. Quelle valeur
approchée entière de s
peut-on proposer ?
(104-84) / s
=1-0,16=0,84 ; 20 / s
=0,9946 d'après les tables ; s
= 20 / 0,9946 ~20.
2. On note Z la
variable aléatoire définie par Z =(X −84)/ s.
a. Quelle est la
loi de probabilité suivie par Z ?
Loi normale centrée réduite N( 0 ;1 ).
b. Justifier que
P(X <=64) = P(Z <= −20 /s).
Z
<=(64 −84)/ s
; Z <= -20 / s.
c. En
déduire la valeur de s,
arrondie à 10−3.
P(Z
<= 20 / s) =1- 0,16 =0,84 ;
20 / s=
0,9946, d'après les tables.
s
=20 / 0,9946 =20,109.
3.
Dans cette question, on considère que s = 20,1.
Les probabilités demandées seront arrondies à 10−3.
a. Calculer la
probabilité que la durée de vie du lave-vaisselle soit comprise entre 2
et 5 ans.
2 ans = 24 mois ; 5 ans = 60 mois.
(24-84) /20,1= -2,985 ; (60-84) / 20,1 = -4,179.
P(Z <= -2,985 )= 0,001418 ; P(Z
> -4,179 )= 1- 0,11623 =0,88377
Probabilité que la durée de vie soit comprise entre 2 et 5 ans :
1-(0,001418+0,88377)=0,115.
b. Calculer la probabilité que le
lave-vaisselle ait une durée de vie supérieure à 10 ans.
10 ans = 120 mois ; (120-84) / 20,1 = 1,791.
P(Z <=1,791) =0,96336 ;
Probabilité que la durée de vie soit supérieure à 10 ans : 1-0,96336 ~ 0,037.
Partie B. Étude de l’extension
de garantie d’El’Ectro
Le lave-vaisselle est garanti gratuitement pendant les deux premières
années.
L’entreprise El’Ectro propose à ses clients une extension de garantie
de 3 ans supplémentaires.
Des études statistiques menées sur les clients qui prennent l’extension
de garantie montrent que 11,5% d’entre eux font jouer l’extension de
garantie.
1. On choisit au
hasard 12 clients parmi ceux ayant pris l’extension de garantie (on
peut assimiler ce choix à un tirage au hasard avec remise vu le grand
nombre de clients).
a. Quelle est la
probabilité qu’exactement 3 de ces clients fassent jouer cette
extension de garantie ? Détailler la démarche en précisant la loi de
probabilité utilisée. Arrondir à 10−3..
On note Y la
variable aléatoire donnant le nombre de clients ayant pris l'extension
de garantie.
Les tirages étant indépendants
et de même probabilité p = 0,115, Y suit
une loi binomiale de paramètres n = 12 ; p = 0,115 ; q = 1-p =0,885.
P(Z=3) = C123 x 0,1153 x0,8859 = 12 x 11
x10 / 6 x 0,1153
x0,8859 ~0,111.
b.
Quelle est la probabilité qu’au moins 6 de ces clients fassent jouer
cette extension de garantie ? Au moins 6 signifie 6 ; 7 ; 8 ; 9 ; 10 ;
11 ; 12.
P( moins de 6 clients utilisent l'extension ) = 0,99885 ;
P (au moins six clients utilisent cette extension) = 1-0,99885 =
0,00115 ~0,001.
2. L’offre
d’extension de garantie est la suivante : pour 65 euros
supplémentaires, El’Ectro remboursera au client la valeur initiale du
lave-vaisselle, soit 399 euros, si une panne irréparable survient entre
le début de la troisième année et la fin de la cinquième année. Le
client ne peut pas faire jouer cette extension de garantie si la panne
est réparable.
On choisit au hasard un client parmi les clients ayant souscrit
l’extension de garantie, et on note Y la variable aléatoire qui
représente le gain algébrique en euros réalisé sur ce client par
l’entreprise El’Ectro, grâce à l’extension de garantie.
a. Justifier que Y prend les valeurs
65 et −334 puis donner la loi de probabilité de Y.
Absence de panne irréparable : Y = 65 € ; probabilité de
cet événement 1-0,115=0,885.
existence d'une panne irréparable :65 -399 = -334 € ;
probabilité de cet événement : 0,115
b. Cette offre
d’extension de garantie est-elle financièrement avantageuse pour
l’entreprise ? Justifier.
E(Y) = 0,885 x 65 +0,115 x(-334) =57,525 -38,41 ~19,11 € par client.
Donc avantage à l'entreprise.
|
| .
. |
|
|
Liban.
En
prévision d’une élection entre deux candidats A et B, un institut de
sondage recueille les intentions de vote de futurs électeurs.
Parmi
les 1 200 personnes qui ont répondu au sondage, 47% affirment vouloir
voter pour le candidat A et les autres pour le candidat B. Compte-tenu
du profil des candidats, l’institut de sondage estime que 10% des
personnes déclarant vouloir voter pour le candidat A ne disent pas la
vérité et votent en réalité pour le candidat B, tandis que 20% des
personnes déclarant vouloir voter
pour le candidat B ne disent pas la vérité et votent en réalité pour le
candidat A.
On choisit au hasard une personne ayant répondu au sondage et on note :
• A l’évènement « La personne interrogée affirme vouloir voter pour le
candidat A » ;
• B l’évènement « La personne interrogée affirme vouloir voter pour le
candidat B » ;
• V l’évènement « La personne interrogée dit la vérité ».
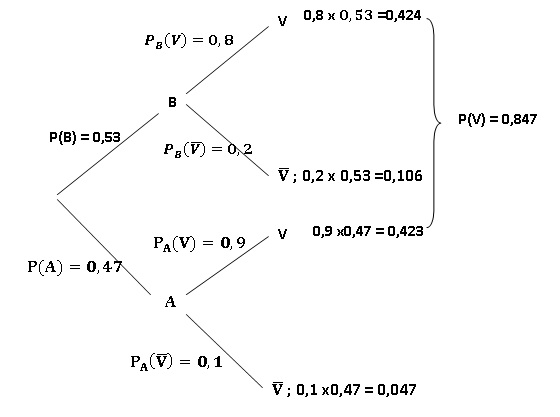
1. Construire un
arbre de probabilités traduisant la situation.
2. a. Calculer la
probabilité que la personne interrogée dise la vérité.
b. Sachant que la
personne interrogée dit la vérité, calculer la probabilité qu’elle
affirme vouloir voter pour le candidat A.
0,423 / 0,847 = 0,499.
3. Démontrer que la
probabilité que la personne choisie vote effectivement pour le candidat
A est 0,529.
P( personne disant la vérité et votant A) + P(persone disant voter B en
mentant) =0,423 + 0,106=0,529.
4. L’institut de
sondage publie alors les résultats suivants :
52,9% des électeurs voteraient pour le candidat A.
Au seuil de confiance de 95%, le candidat A peut- il croire en sa
victoire ?
Les conditions d'application sont bien vérifiées n = 1200
>30 ; np = 1200 x0,529 =634,5 > 5 et n(1-p) = 1200
x(1-0,529)=565,2 >5.
1 / racine carrée (1200) = 0,02887.
Intervalle de confiance [0,529-0,0227 ; 0,529 +0,02887] soit [0,5001 ;
0,5579].
La borne inférieure est supérieure à 0,5, A peut croire en sa victoire,
au seuil de confiance de 95%.
5. Pour effectuer
ce sondage, l’institut a réalisé une enquête téléphonique à raison de
10 communications par demi-heure. La probabilité qu’une personne
contactée accepte de répondre à cette enquête est 0,4. L’institut de
sondage souhaite obtenir un échantillon de 1 200 réponses.
Quel temps moyen, exprimé en heures, l’institut doit-il prévoir pour
parvenir à cet objectif ?
8 personnes acceptent de répondre à chaque heure : 1200 / 8 = 150
heures.
|
|
|
|
Amérique du Nord.
Une
entreprise fabrique des tablettes de chocolat de 100 grammes. Le
service de contrôle qualité effectue plusieurs types de contrôle.
Partie A Contrôle
avant lamise sur lemarché
Une tablette de chocolat doit peser 100 grammes avec une tolérance de
deux grammes en plus ou en moins. Elle est donc mise sur le marché si
sa masse est comprise entre 98 et 102 grammes. La masse (exprimée en
grammes) d’une tablette de chocolat peut être modélisée par une
variable aléatoire X suivant la loi normale d’espérance µ = 100 et
d’écart-type s =
1. Le réglage des machines de la chaîne de fabrication permet de
modifier la valeur de s.
1. Calculer la
probabilité de l’évènement M : « la tablette est mise sur le marché ».
P(X inférieure ou égale à 98) = 0,0228 ; P( X supérieure ou égale à
102) =0,0228.
probabilité que la tablette soit mise sur le marché =1-0,0228-0,0228=0,9544.
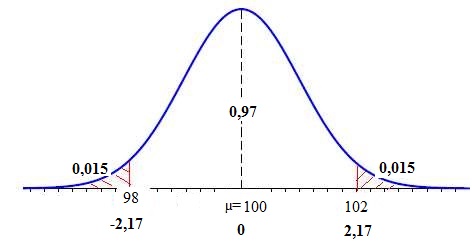
2. On souhaite
modifier le réglage des machines de telle sorte que la probabilité de
cet évènement atteigne 0,97.
Déterminer la valeur de s
pour que la probabilité de l’évènement « la tablette est mise sur le
marché » soit égale à 0,97.
On pose Z =( X-µ) / s
; (98-100) / s =
-2 / s ;
(102-100) / s = 2
/ s = 2,17,
d'après les tables ; s
= 2 / 2,17 =0,9216.
Partie B. Contrôle
à la réception
Le service contrôle la qualité des fèves de cacao livrées par les
producteurs. Un des critères de qualité est le taux d’humidité qui doit
être de 7%. On dit alors que la fève est conforme.
L’entreprise a trois fournisseurs différents : le premier fournisseur
procure la moitié du stock de fèves, le deuxième 30% et le dernier
apporte 20% du stock.
Pour le premier, 98%de sa production respecte le taux d’humidité ; pour
le deuxième, qui est un peu moins cher, 90% de sa production est
conforme, et le troisième fournit 20% de fèves non conformes.
On choisit au hasard une fève dans le stock reçu. On note Fi
l’évènement « la fève provient du fournisseur i », pour i prenant les
valeurs 1, 2 ou 3, et C l’évènement « la fève est conforme ».
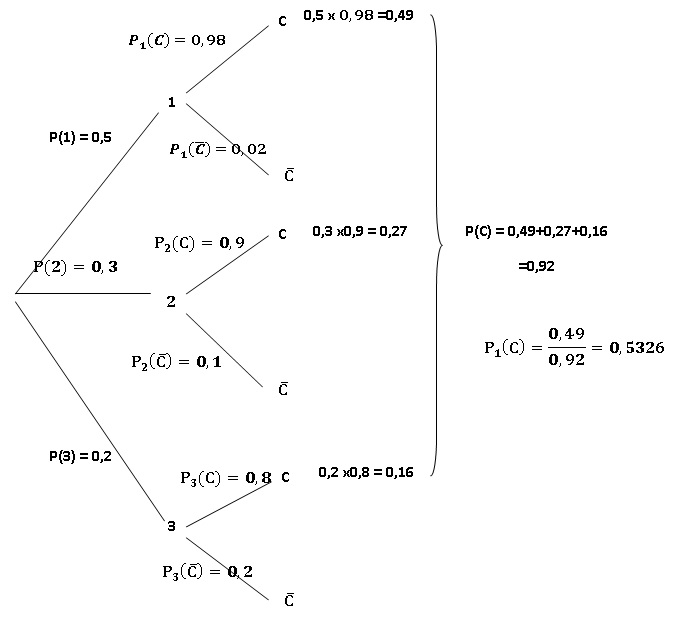
1. Déterminer la
probabilité que la fève provienne du fournisseur 1, sachant qu’elle est
conforme. Le résultat sera arrondi à 10−2.
2.
Le troisième fournisseur ayant la plus forte proportion de fèves non
conformes, L’entreprise décide de ne conserver que les fournisseurs 1
et 2. De plus, elle souhaite que 92% de fèves qu’elle achète soient
conformes. Quelle proportion p de fèves doit-elle acheter au
fournisseur 1 pour atteindre cet objectif ?
0,98 p + 0,90(1-p)=0,92 ; 0,08 p =0,02 ; p = 0,25.
|
|
Centres Etrangers.
Un
fournisseur produit deux sortes de cadenas. Les uns sont premier prix,
et les autres sont haut de gamme. Un magasin de bricolage dispose d’un
stock de cadenas
provenant de ce fournisseur ; ce stock comprend un grand nombre de
cadenas de chaque type.
Partie A.
1. Le fournisseur
affirme que, parmi les cadenas haut de gamme, il n’y a pas plus de 3%
de cadenas défectueux dans sa production. Le responsable du magasin de
bricolage désire vérifier la validité de cette affirmation dans son
stock ; à cet effet, il prélève un échantillon aléatoire de 500 cadenas
haut de gamme, et en trouve 19 qui sont défectueux.
Ce contrôle remet-il en cause le fait que le stock ne comprenne pas
plus de 3% de cadenas défectueux ?
On utilise un intervalle de fluctuation asymptotique au seuil de
95%.
1,96 x(0,03 x0,97 / 500 )½ =0,01495 ; I =[0,03-0,01495 ;
0,03 +0,01495] soit [0,015 ; 0,045 ] ; 19 / 500 =0,038, cette valeur
appartient à l'intervalle de fluctiation : le contrôle ne remet pas en
cause le fait que le stock ne comprenne pas plus
de 3% de cadenas défectueux.
2. Le responsable
du magasin souhaite estimer la proportion de cadenas défectueux dans
son
stock de cadenas premier prix. Pour cela il prélève un échantillon
aléatoire de 500 cadenas premier prix, parmi lesquels 39 se révèlent
défectueux. Donner un intervalle de confiance de cette proportion au
niveau de confiance 95%.
Fréquence de cadenas défectueux : f = 39/500 = 0,078.
n = 500 >30 ; nf = 500 x0,078 = 39 >5 ; 500 x(1-0,078) =
461 >5. Les trois conditions sont vérifiées.
1 /500½ = 0,0447 ; I = [0,078 -0,0447 ; 0,078+0,0447] soit
[0,033 ; 0,123 ].
Partie B :
D’après une étude statistique faite sur plusieurs mois, on admet que le
nombre X de cadenas premier prix vendus par mois dans le magasin de
bricolage peut être
modélisé par une variable aléatoire qui suit la loi normale de moyenne
µ = 750 et d’écart-type s
= 25.
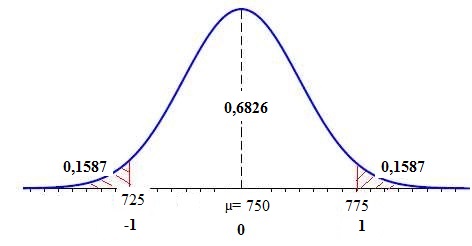
1. Calculer P(725
<= X <=775).
Loi normale centrée réduite : (725-750) / 25 = -1 ; (775-750) / 25 = 1.
2. Le responsable
du magasin veut connaître le nombre n de cadenas premier prix qu’il
doit avoir en stock en début de mois, pour que la probabilité d’être en
rupture de stock en cours de mois soit inférieure à 0,05. On ne
réalimente pas le stock en cours de mois. Déterminer la plus petite
valeur de l’entier n remplissant cette condition.
P(X>n)<0,05. P (X inférieure ou égal à n) doit être supérieur ou
égal à 0,95.
Les tables donnent (n-750) / 25 = 1,645 ; n = 1,645 x25 +750 ~ 792
Partie
C : On admet maintenant que, dans le magasin :
• 80% des cadenas proposés à la vente sont premier prix, les autres
haut de gamme ;
• 3% des cadenas haut de gamme sont défectueux ;
• 7% des cadenas sont défectueux.
On prélève au hasard un cadenas dans le magasin. On note :
• p la probabilité qu’un cadenas premier prix soit défectueux ;
• H l’évènement : « le cadenas prélevé est haut de gamme » ;
• D l’évènement : « le cadenas prélevé est défectueux ».
1. Représenter la
situation à l’aide d’un arbre pondéré.
2. Exprimer en
fonction de p la probabilité P(D). En déduire la valeur du réel p. Le
résultat obtenu est-il cohérent avec celui de la question A - 2. ?
p
=(0,07 -0,006 ) / 0,8 =0,08 , cette valeur appartient bien à
[0,033 ; 0,123 ]. ce ésultat est donc ochérent.
3.
Le cadenas prélevé est en bon état. Déterminer la probabilité que ce
soit un cadenas haut de gamme.
P( le cadenas est en bon état) = (1-p) x0,8 + 0,2 x0,97 =0,736 +
0,194=0,93.
P ( un cadenas haut de gamme est en bon état) = 0,194 / 0,93 = 0,2086
~0,209.
Polynésie.
Dans un pays, la
taille en centimètres des femmes de 18 à 65 ans peut être modélisée par
une variable aléatoire X1 suivant la loi normale d’espérance
μ1 = 165 cm et
d’écart-type s1
= 6 cm, et celle des hommes de 18 à 65 ans, par une variable aléatoire X2
suivant la loi normale d’espérance μ2 = 175 cm et
d’écart-type s2
= 11 cm.
Dans cet exercice tous les résultats seront arrondis à 10−2
près.
1. Quelle est la
probabilité qu’une femme choisie au hasard dans ce pays mesure entre
1,53 mètre et 1,77 mètre ?
2. a. Déterminer la probabilité qu’un homme choisi au hasard
dans ce pays mesure plus de 1,70 mètre.
Loi normale centrée réduite : pour les
femmes : (153-165) / 6= -2 ; (177-165)/6=+2 ;
pour les hommes : (170-175)/11= -0,455.
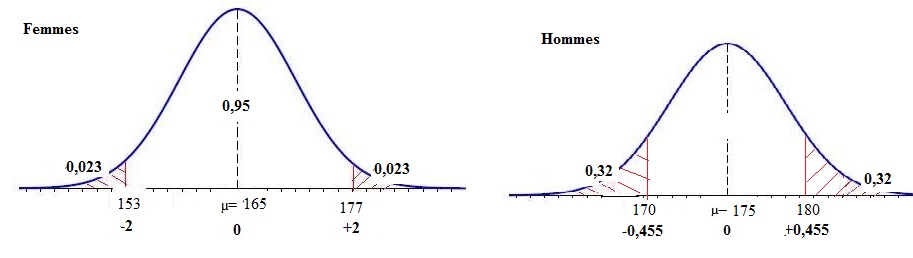
Probabilité
qu’une femme choisie au hasard dans ce pays mesure entre 1,53 mètre et
1,77 mètre : 0,95.
Probabilité qu’un homme choisi au hasard
dans ce pays mesure plus de 1,70 mètre : 1-0,32 = 0,68.
2.b.
De plus, on sait que dans ce pays les femmes représentent 52% de la
population des personnes dont l’âge est compris entre 18 et 65 ans. On
choisit
au hasard une personne qui a entre 18 et 65 ans. Elle mesure plus de
1,70 m. Quelle est la probabilité que cette personne soit une femme ?
On note les événements : H " la personne est un homme" et D " la
personne mesure plus de 1,70 m".
Probabilité qu'une femme mesure plus de 1,70 m ; (170-165) / 6=0,833.
Les tables donnent : 1-0,797=0,203 ~0,20.
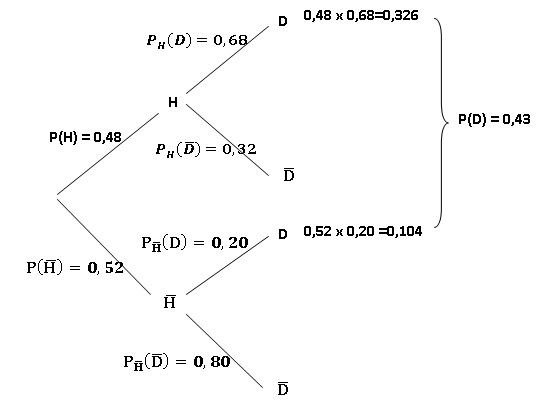
Probabilité que la persone soit une femme mesurant plus de 1,70 m :
0,104 / 0,43 =0,24.
Antilles septembre.
Dans un supermarché, on réalise une étude sur la vente de bouteilles de
jus de fruits sur une période d’un mois.
• 40% des bouteilles vendues sont des bouteilles de jus d’orange ;
• 25% des bouteilles de jus d’orange vendues possèdent l’appellation «
pur jus ».
Parmi les bouteilles qui ne sont pas de jus d’orange, la proportion des
bouteilles de « pur jus » est notée x, où x est un réel de l’intervalle
[0 ; 1].
Par ailleurs, 20%des bouteilles de jus de fruits vendues possèdent
l’appellation «pur jus ».
On prélève au hasard une bouteille de jus de fruits passée en caisse.
On définit les évènements suivants :
R : la bouteille prélevée est une bouteille de jus d’orange ;
J : la bouteille prélevée est une bouteille de « pur jus ».
Partie A.
1. Représenter
cette situation à l’aide d’un arbre pondéré.
2. Déterminer la
valeur exacte de x.
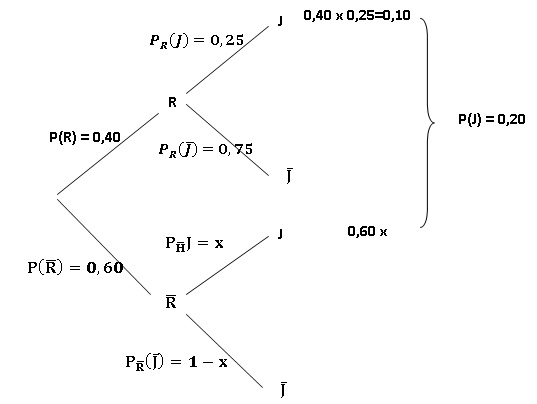
0,10+0,60 x =0,20 ; x = 1 / 6.
3. Une bouteille
passée en caisse et prélevée au hasard est une bouteille de «pur jus ».
Calculer la probabilité que ce soit une bouteille de jus d’orange.
0,10 / 0,20 = 0,5.
Partie B.
Afin d’avoir une meilleure connaissance de sa clientèle, le directeur
du supermarché fait une étude sur un lot des 500 dernières bouteilles
de jus de fruits vendues.
On note X la variable aléatoire égale au nombre de bouteilles de « pur
jus » dans ce lot.
On admettra que le stock de bouteilles présentes dans le supermarché
est suffisamment important pour que le choix de ces 500 bouteilles
puisse être assimilé à un
tirage au sort avec remise.
1. Déterminer la
loi suivie par la variable aléatoire X. On en donnera les paramètres.
Les tirages étant indépendants et de même probabilité p = 0,2, X suit
une loi binomiale de paramètres n = 500 ; p = 0,2 ; q = 1-p =0,8.
2.
Déterminer la probabilité pour qu’au moins 75 bouteilles de cet
échantillon de 500 bouteilles soient de « pur jus ». On arrondira le
résultat au millième.
Espérance : np = 500 x0,2 = 100 ; variance npq = 500 x0,2 x0,8=80.
Probabilité pour qu'au plu 74 bouteilles ne soient pas de pur jus =
0,001627, d'après les tables ou la calculatrice.
Probabilité pour qu’au moins 75 bouteilles
de cet échantillon de 500 bouteilles soient de « pur jus » =
1-0,001627~0,998.
Partie C.
Un fournisseur assure que 90% des bouteilles de sa production de pur
jus d’orange contiennent moins de 2% de pulpe. Le service qualité du
supermarché prélève un
échantillon de 900 bouteilles afin de vérifier cette affirmation. Sur
cet échantillon, 766 bouteilles présentent moins de 2% de pulpe.
1. Déterminer
l’intervalle de fluctuation asymptotique de la proportion de bouteilles
contenant moins de 2% de pulpe au seuil de 95%.
n = 900 >30 ; p = 0,9 ; np = 0,9 x900 = 810 >5 ; n(1-p) = 900
x0,1 = 90 > 5 ; les conditions sont remplies :
1,96 (pq / n)½ =1,96 (0,9 x0,1 / 900)½=0,0196 ;
Intervalle de fluctuation : [0,90 -0,0196 ; 0,90 +0,0196] soit [0,880 ;
0,920 ]
2. Que penser de
l’affirmation du fournisseur ?
766 / 900=0,851, cette valeur n'appartient pas à l'intervalle de
fluctuation. L'affirmation du fournisseur est fausse.
Polynésie septembre.
Partie A.
On étudie une maladie dans la population d’un pays. On a constaté que
le taux, en nanogrammes par millilitre (ng.mL−1), d’une
substance Gamma présente dans le
sang est plus élevé chez les personnes atteintes de cette maladie que
chez les personnes qui n’en sont pas atteintes.
1. Le taux de cette
substance Gamma dans la population des personnes qui ne sont pas
atteintes par la maladie est modélisé par une variable aléatoire T qui
suit la loi normale d’espérance μ = 40 et d’écart-type s = 8.
On choisit au hasard une personne parmi celles qui ne sont pas
atteintes par la maladie étudiée.
Calculer la probabilité que le taux dans le sang de la substance
Gamma soit supérieur à 60 ng.mL−1.
Loi normale centrée réduite : (60-40) / 8=2,5.
P(taux substance Gamma supérieure à 60 ng L-1) = 1 - P( taux
substance Gamma inférieure ou égale à 60 ng L-1) = 1-0,9938
~0,0062.
2.
Des études ont mis en évidence que le taux moyen de la substance Gamma
chez les personnes atteintes par la maladie étudiée est de 50 ng.mL−1
et que 10% d’entre elles ont un taux de substance Gamma inférieur à 43
ng.mL−1. On appelle T ′ la variable aléatoire quimodélise le
taux de la substance Gamma en ng.mL−1 chez une personne
atteinte par la maladie étudiée.
On admet que T ′ suit la loi normale d’espérance μ′ et d’écart-type s′. Préciser la valeur de μ′
et déterminer la valeur de σ′.
µ' = 50 ng.mL−1 . On pose Z = (43-50)
/ s' ; Z
suit la loi normale centrér réduite N(0 ; 1 ).
P(Z inférieur ou égal à -7 / s')
= 0,1. Les tables ou la calculatrice donne -7
/ s' = -1,282 ; s' =7/1,282 =5,46.
Partie B.
Pour dépister chez une personne la maladie étudiée, on effectue une
prise de sang. On considère que le dépistage est positif si le taux de
la substance Gamma est supérieur
ou égal à 45 ng.mL−1. Une personne étant choisie au hasard
dans la population, on appelle :
• M l’évènement « le patient est atteint par la maladie étudiée » ;
• D l’évènement « le patient a un dépistage positif ».
On admet que :
• 82% des personnes atteintes par la maladie étudiée ont un dépistage
positif ;
• 73% des personnes non atteintes par cette maladie ont un dépistage
négatif.
On sait de plus que 10% de la population étudiée est atteinte par cette
maladie.
1. Démontrer que
la probabilité qu’un patient ait un dépistage positif est de 0,325.
2. Calculer la
probabilité qu'un patient ayant un dépistage négatif soit malade.
Interpréter ce résultat.
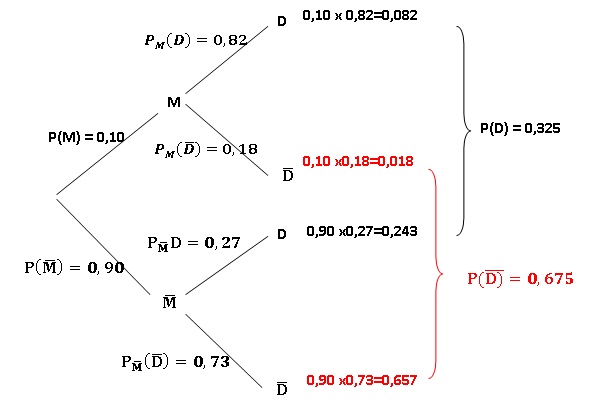
La probabilité qu'un patient ayant un
dépistage négatif soit malade est égale à 0,018 / 0,675 = 0,0267.
3.
Un patient a un dépistage positif. Le médecin le rassure en lui
indiquant qu’il n’a qu’une chance sur quatre d’avoir contracté la
maladie. Qu’en pensez-vous ?
1-0,243 / 0,325=0,252 ( 25,2 %).
Il a un peu plus d'une chance sur quatre
d’avoir contracté la maladie.
Partie C.
Lors du dépistage précédent, la prise de sang est effectuée chez des
sujets à jeun. Les données montrent que 82% des patients malades ont un
dépistage positif.
Pour améliorer le confort des personnes susceptibles de subir cet
examen sanguin, on souhaite vérifier si le fait d’être à jeun est une
condition indispensable dans le
protocole. On considère un groupe de 300 personnes malades sur
lesquelles la prise de sang n’est pas effectuée à jeun. Le dépistage se
révèle positif pour 74% d’entre elles.
Ce dépistage peut-il être effectué sur des personnes qui ne sont pas à
jeun ?
n = 300 >30 ; np = 300 x0,82 =246 >5 ; n(1-p) = 300 x0,18 =54
>5. Les conditions sont vérifiées pour déterminer un intervalle de
fluctuation.
1,96 (pq / n)½ = 1,96(0,82 x0,18 /300)½=0,0435.
Intervalle de fluctuation : [0,82 -0,0435 ; 0,82 +0,0435 ) soit [ 0,776
;0,863 ].
0,74 n'appartient pas à cet intervalle. Le dépistage doit se faire sur
des personnes à jeun.
Nlle Calédonie mars 2016.
Partie A
Une boite contient 200 médailles souvenir dont 50 sont argentées, les
autres dorées. Parmi les argentées 60% représentent le château de
Blois, 30% le château de Langeais,
les autres le château de Saumur. Parmi les dorées 40% représentent le
château de Blois, les autres le château de Langeais.
On tire au hasard une médaille de la boite. Le tirage est considéré
équiprobable et on note :
A l’évènement « la médaille tirée est argentée » ;
D l’évènement « la médaille tirée est dorée » ;
B l’évènement « lamédaille tirée représente le château de Blois » ;
L l’évènement « la médaille tirée représente le château de Langeais » ;
S l’évènement « la médaille tirée représente le château de Saumur ».
1. Dans cette question, on donnera les résultats
sous la forme d’une fraction irréductible.
a. Calculer la
probabilité que la médaille tirée soit argentée et représente le
château de Langeais.
b. Montrer que la
probabilité que la médaille tirée représente le château de Langeais est
égale à 21 /40.
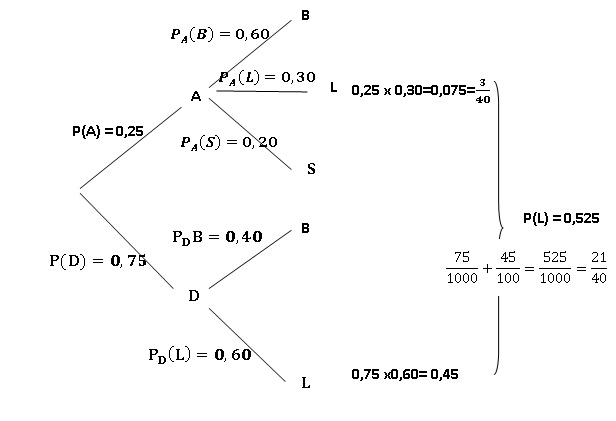
c. Sachant que la
médaille tirée représente le château de Langeais, quelle est la
probabilité que celle-ci soit dorée ?
( 9 / 20) / (21 / 40) = 18 /21 = 6 /7.
2. Sachant que la
médaille tirée représente le château de Saumur, donner la probabilité
que celle-ci soit argentée.
Cette probabilité est égale à 1, il n'y a pas de médaille dorée
représentant Saumur.
Partie B.
Une médaille est dite conforme lorsque sa masse est comprise entre 9,9
et 10,1 grammes.
On dispose de deux machines M1 et M2 pour
produire les médailles.
1. Après plusieurs
séries de tests, on estime qu’une machine M1 produit des
médailles dont la masse X en grammes suit la loi normale d’espérance 10
et d’écart-type 0,06.
On note C l’évènement « la médaille est conforme ».
Calculer la probabilité qu’une médaille produite par la machine M1
ne soit pas conforme. On donnera le résultat arrondi à 10−3
près.
On pose Z = (X-10) / 0,06. Z suit la loi normale centrée réduite N(0 ;
1). (10,1-10) /0,06 =1,667.
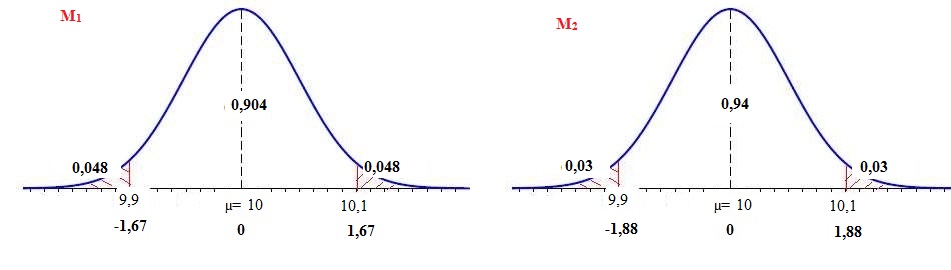
La probabilité qu’une médaille produite
par la machine M1 ne soit pas conforme vaut : 0,048+0,048 =
0,096.
2. La proportion
des médailles non conformes produites par la machine M1 étant
jugée trop importante, on utilise une machine M2 qui produit
des médailles dont la masse Y en grammes suit la loi normale
d’espérance μ = 10 et d’écart-type s.
a. Soit Z la
variable aléatoire égale à (Y −10) /s.
Quelle est la loi suivie par la variable Z ?
Z suit la loi normale centrée réduite N(0
; 1).
b.
Sachant que cette machine produit 6% de pièces non conformes,
déterminer la valeur arrondie au millième de s.
(10,1-10) / s =
1,88 ; s
=0,1/1,88 ~0,053.
|
|