QCM mathématiques.
Concours cycle de formation des officiers de 1ère classe de la marine
marchande 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Barème
: +1 pour une réponse correcte ; -1 pour une réponse incorrecte ;
0 en absence de réponse ; bonification d'un point pour tout
exercice intégralement et correctement traité.
Exercice 1.
f désigne la fonction numérique définie sur R par :
f(x) = e-x ln ( 1+ex).
1.
f '(x) +f(x) = ex /(1+ex). Faux.
Calcul de f '(x) : on pose u = e-x ; v = ln(1+ex)
; u' = -e-x ; v' = ex /(1+ex).
f '(x) = u'v +v'u = -e-x ln ( 1+ex)+1
/(1+ex).
f '(x) +f(x) =1 /(1+ex).
2. On admet que
pour tout réel u >0,
ln(1+u) > u /(1+u).
Grâce à cette inégalité, il est possible de préciser le sens de
variation de f sur R. Vrai.
f '(x) = -e-x[ ln ( 1+ex)-ex
/(1+ex)].
On pose u = ex : f
'(u) = -1/ u [ ln ( 1+u)-u
/(1+u)].
ln(1+u) > u /(1+u) et u est
positif , donc f '(u) est négatif.
f(x) est décroissante sur R.
3. g désigne une
fonction numérique définie et dérivable sur R telle que : g'(x) +g(x) =
ex /(1+ex).
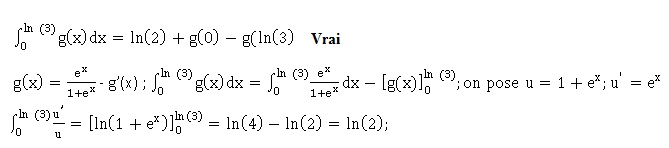
Exercice 2. Soit g la fonction définie sur ]0 ; +oo[ par. g(x) =
1 / ( x e(1/x))-x.
1.
A la question " déterminer la limite de x e(1/x) quand x
tend vers zéro par valeur positive", un élève a tenu le raisonnement
suivant :
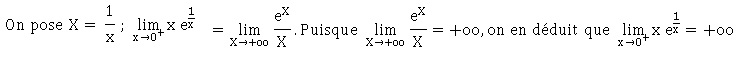
Ce raisonnement est incorrecte.
Faux.
2. On admet que g est strictement décroissante sur ]0 : +oo[.
On note f la fonction définie sur ]0 ; +oo[ par : f(x) = 1 /(2x e(1/x)
).
Pour tout x >0, 0 <
f(x) < 0,5 x. Vrai
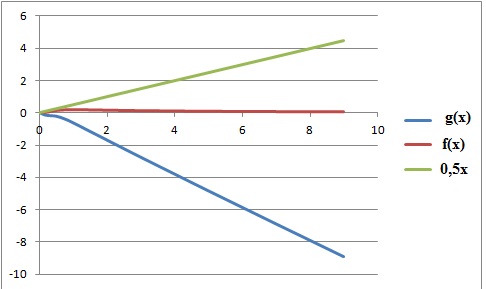
f(x) =0,5 g(x) +0,5x.
f(0) =0 ; g(0) = 0 ; g est strictement décroissante.
3. Soit (un)
la suite numérique définie par : u0 = 2
et un+1 = f(un) avec n entier.
Si 0 <f(x) <0,5 x pour tout x
>0, alors 0 <un
<1 /2n-1
et (un) converge. Vrai.
u1 = f(u0) = f(2) =e-0,5 / 22~0,606
/ 22 ~0,303 / 2.
Initialisation
: 0 < f(un-1) <
0,5 un-1 ; 0 < un <
0,5 un-1 ; 0 < u1 <
0,5 u0 ; 0 < u1 <
1 / 20.
La propriété est vraie au rang 1.
Hérédité :
la propriété est supposée vraie au rang p. 0 < up < 1 /2p-1 .
up+1
= f(up) ; 0 < f(up) < up / 2
; 0 < up+1 < up / 2 ; 0 < up+1 < 1 / 2p.
Conclusion
: la propriété étant vrai au rang 1 et héréditaire, la propriété est
vrai pour tout n entier.
1 / 2p tend
vers zéro si p tend vers l'infini : la suite (un) converge.
Exercice 3.
(un) désigne une suite numérique telle que u0 =0
et u1 = 1. On considère la suite numérique ( vn)
définie par :
vn = un-un+1, quel que soit n entier.
1.

2. Si (vn)
est une suite géométrique de raison q comprise entre ]-1 ; +1[,
alors (un) est une suite convergente. Faux.
un = -v0(1-qn-1) / (1-q) = (1-qn-1) / (1-q) .
qn-1 tend vers zéro si n tend
vers l'infini et un tend vers 1 / (1-q).
Si q tend vers 1, alors un tend vers l'infini.
3. (un)
désigne désormais la suite définie par : u0 = 0 ; u1
= 1 ; un+2 = aun+1 +(1-a)un, où a est
une constante réelle comprise dans l'intervalle ]0 ; 1 [.
(vn) est une suite géométrique convergente. Faux.
vn = un-un+1 ; un+1
= aun +(1-a)un-1 ;
vn =(1-a)un
-(1-a)un-1 =(1-a)(un -un-1 )=(a-1)(un-1-un)
=(a-1) vn-1.
Il s'agit d'une suite géométrique de raison ( a-1) et de premier terme v0
= u0-u1 = -1.
vn = -(a-1)n ; a-1 est négatif, compris dans
l'intervalle ] -1 ; 0 [ .
Si a = 0,0001 : (a-1)200
~0,98 ;
(a-1)201
~ -0,98.
La suite (vn) ne converge pas.
|
| .
. |
|
|
Exercice 4.
Pour tout entier naturel n, on note :
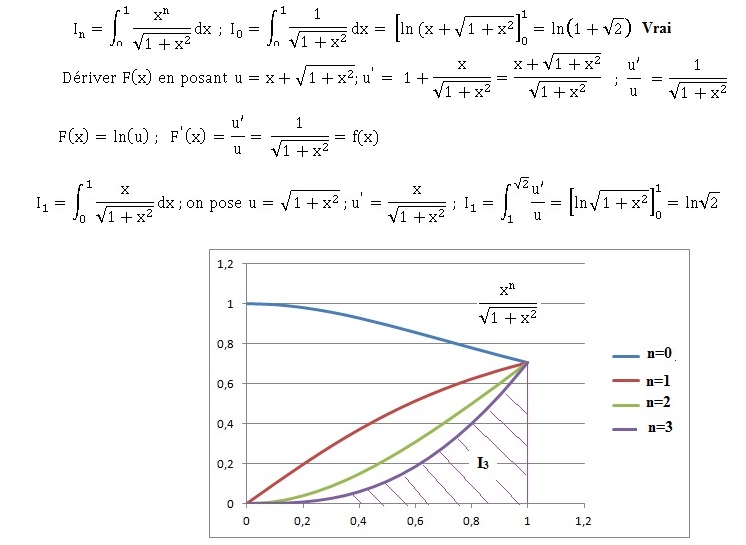
2. (In)
est une suite croissante. Faux.
L'aire comprise entre la courbe, la droite d'équation x=0, la droite
d'équation x=1 et la droite d'équation y=0, diminue quand n croît.
3. (In) est une suite convergente. Vrai.
Exercice 5.
f désigne une fonction numérique, impaire, définie et continue sur R,
dont le tableau des variations sur [0 ; +oo[ est le suivant :
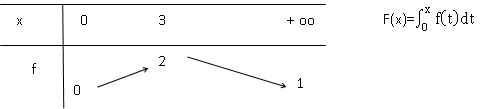
1. F est une
fonction croissante sur [0 ; +oo[. Faux.
f(x) est croissante sur [0 ; 3 ] et décroissante pour x >3. Il en
est de même de F.
2. F(1) =F(-1). Faux.
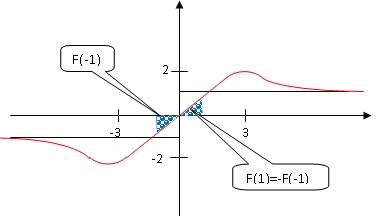
3. Quand x tend
vers plus l'infini, F(x) tend vers l'infini. Vrai.
F(x) représente
l'aire de la surface comprise entre la courbe, la droite d'équation x=0
et l'axe des abscisses.
Exercice 6.
Le plan complexe est muni d'un repère orthonormé direct. q désigne un élément de
l'intervalle ]- p/2
; p/2 [.
On note z0 le nombre complexe défini par : z0 = 1
+exp(2iq).
1. Une écriture
exponentielle de z0 est z0 = 2 cos (q) exp(iq). Vrai.
z0 = 1 +cos(2q)
+i sin (2q).
| z0 |2 =(1 +cos(2q) )2+sin2
(2q)= 2+2cos(2q) = 4cos2(q) ; |z0|=
2 cos (q).
z0 / |z0|=
cos a + i sin a = (1
+cos(2q)) / (2 cos (q))
+i sin (2q) /(2 cos (q)).
On identifie : cos a =
(1
+cos(2q)) / (2 cos (q)) = cos(q) ;
sin
(2q) /(2 cos (q))
= 2 sin(q) cos (q) / (2 cos (q))
= sin (q).
2. Si q = p/6, z02013
est un nombre réel. Faux.
[2 cos (p/6)]2013 exp(i
2013p /6)
;
2013p
/6
=335,5 p =167 x(2p) +1,5 p.
3. z0 = 4 /z0
si et seulement si q
= 2kp avec k
appartenant à Z. Faux.
z0 = ±2 ; 2 cos (q) exp(iq) = ± 2 ; cos (q) exp(iq) = ± 1.
cos (q) (cos (q) +i sin (q)) = ±1 ; sin
(q) = 0 ; q = k p.
|
Exercice 10.
Le temps d'attente en minutes à l'un quelconque des
comptoirs
d'enregistrement d'un aéroport, peut être mpdélisé par une variable
aléatoire suivant une loi exponentielle de paramètre l = 0,04.
1. Le temps moyen
d'attente à l'un des comptoirs est de 25 minutes. Vrai.
1 / 0,04 = 25 min.
2.
Un client a déja attendu 20 minutes à un comptoir. La probabilité qu'il
soit reçu dans les 5 minutes suivantes n'excède pas 0,2. Vrai.
La
loi exponentielle modèlise la durée de vie d'un phénomène sans mémoire.
Le fait que le phénomène ait duré pendant t heures ne change rien à son
espérance de vie à partir de l'instant t.
P(X<5)=1-exp(-0,04 x5) = 1-exp(-0,2) = 1-0,819 ~0,18.
3.
Huit comptoirs sont ouverts et le temps d'attente à un comptoir est
indépendant du temps d'attente aux autres. Des comptoirs
supplémentaires sont ouverts lorsque la durée d'attente à au moins 5
des 8 comptoirs est supérieure à 20 minutes. La probabilité que de
nouveaux comptoirs soient ouverts est voisine de 0,26. Faux.
Probabilité d'attendre plus de 20 minutes à un comptoir : exp(-0,04
x20) ~0,45
Probabilité d'attendre plus de 20 minutes : à 2 comptoirs : 0,452=
0,2025 ; à 3 comptoirs : 0,453=0,0911 ; à 4 comptoirs : 0,454=0,041
; total : 0,785.
Probabilité d'ouverture de nouveaux comptoirs : 1-0,785 ~0,22.
Exercice 11.
A la veille d'une élection, deux candidats A et B sont en présence. Un
sondage est réalisé sur un échantillon de 400 électeurs choisis au
hasard dans la circconscription considérée. ( L'ffectif de la
population constituée des électeurs de cette circonscription est
supposé suffisamment grand pour que le prélévement de cet
échantillon puisse être assimilé à un tirage successif et avec remise
des 400 individus dans cette population.
1.
Lors de la précédente consultation électorale, A avait obtenu 51 % des
suffrages exprimés. Le sondage qui vient d'être réalisé, le crédite de
190 intentions de vote.
Au niveau de confiance de 95 %, sa côte de popularité est restée
stable. Vrai.
1 / 400½ =0,05 ; 190 / 400 = 0,475 ; intervalle de
confiance [ 0,475 -0,05 ; 0,475 +0,05 ] soit : [0,425 ; 0,525 ].
0,51 appartient à cet intervalle de confiance.
2. Le candidat B
qui se
présente pour la première fois, est quand à lui, crédité de 208
intentions de vote. Au niveau de confiance de 95 %, le candidat B a
raison de penser que si les élections s'étaient déroulées à la date de
ce sondage, il aurait certainement été élu. Faux.
1 / 400½ =0,05 ; 208 / 400 = 0,52 ; intervalle de
confiance [ 0,52 -0,05 ; 0,52 +0,05 ] soit : [0,47 ; 0,57 ].
3.
p désigne la proportion d'électeurs qui vont effectivement voter
pour B. Au niveau de confiance de 95 %, il aurait fallu réaliser un
sondage sur un échantillon d'effectif au minimum supérieur à 1600 pour
obtenir une esttimation à 5 % près. Vrai.
1/1600½=0,025.
Exercice 12.
L'éppreuve de maths d'un concours
consiste à choisir
3 affirmations parmi 5 proposées, puis à répondre par vrai, faux, je
ne sais pas à ces trois affirmations. Le barême est le suivant :
+1 pour toute réponse correcte, -1 pour toute réponse incorrecte, 0
pour je ne sais pas.
On additionne les points obtenus pour obtenir une note sur trois. Les
candidats complètent le document réponse suivant :
Affirmation
n°
|
Vrai
|
Faux
|
Je
ne sais pas
|
...
|
|
|
|
...
|
|
|
|
...
|
|
|
|
Un candidat n'ayant aucune connaissance en maths, décide de
compléter son document réponse en remplissant la colonne "affirmation
n°" par trois nombres choisis au hasard parmi 1, 2, 3, 4, 5, puis
en cochant au hasard sur chaque ligne, l'une des cases vrai, faux, je
ne sais pas.
1. Sans tenir
compte de l'ordre, il y a dix façons de compléter la colonne de gauche
du tableau précédent. Vrai.
C53 = 5 x4x3 / (2x3) = 10.
2. Ce candidat a
plus d'une chance sur 2 d'avoir une note supérieure ou égale à 1 sur 3.
Faux. 10 / 27 ~0,37.
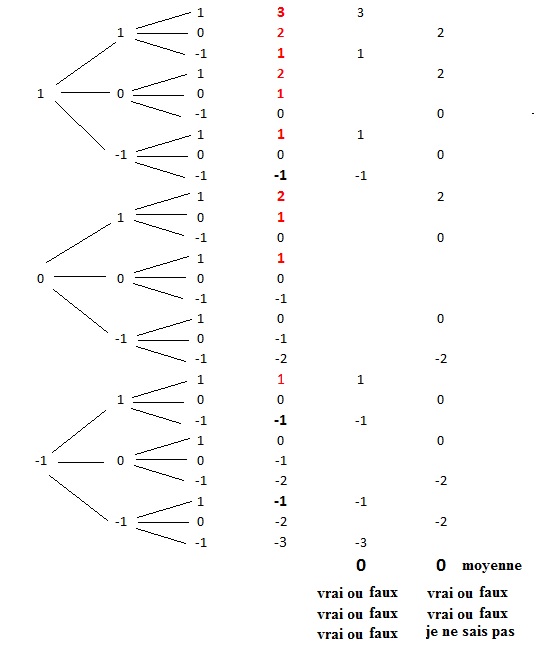
3. En terme
d'espérance, il est plus avantageux pour lui de choisir de ne cocher
que les cases vrai ou faux pour les trois affirmations, que de cocher
la case " je ne sais pas" pour l'une des 3 affirmations et vrai
ou faux pour les deux autres. Faux.
|
|