Mathématiques,
probabilités,
concours Puissance 11. 2015-16
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Exercice 3- 2016. Probabilités conditionnelles.
On joue avec deux dés dont les faces sont numérotées de 1 à 4.
Le premier dé, D1, est un dé « honnête » c'est-à-dire pour lequel la sortie de chacune des faces est équiprobable ;
Le deuxième dé, D2, est truqué de façon que :
• la face numérotée 1 et la face numérotée 4 ont une chance sur douze de sortir ;
• la face numérotée 3 a une chance sur quatre de sortir.
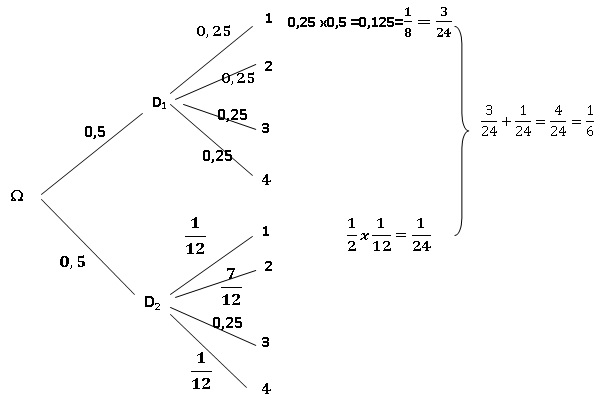
a) On lance le dé n°2 , la probabilité de l'événement « on a obtenu la face numérotée 2 » est égale a 7/12. Vrai.
1-1/4-1/12-1/12=1-5/12 =7/12.
Dans toute la suite, on lance un dé pris au hasard.
b) La probabilité d'obtenir l'événement « on a obtenu la face numérotée 1 » est égale, a, 1/9. Faux.
La probabilité de choisir D1 est de 0,5 et la probabilité d'obtenir 1 avec ce dé est 0,25 ; 0,5 *0,25 = 0,125 = 1 /8.
La probabilité de choisir D2 est de 0,5 et la probabilité d'obtenir 1 avec ce dé est 1 / 12 ; 0,5 *1/12 = 1 /24.
par suite 1 / 24 + 1/8 =4/24 = 1 /6.
c) Les événements « on a obtenu un numéro pair » et « on a utilisé le dé D1 » sont indépendants. Vrai.
Ces événements n'ont aucune influence l'un sur l'autre.
d) Sachant qu 'on a obtenu la face numérotée 1, la probabilité qu 'on ait utilisé le dé D1 est égale à 3/4. Vrai.
Exercice 4- 2016 . Lien entre tableau et arbre de probabilités.
Dans un lycée, les 200 élèves de Terminale se répartissent suivant les 3 activités : sport (S), théâtre (T) etdessin (D).
On donne les informations suivantes :
20 garçons choisissent le théâtre et 34 garçons choisissent le dessin.
28 filles choisissent le sport et 72 filles choisissent le dessin.
Le nombre total de garçons représente 30% de l'effectif total.
Le sport est choisi par 10% des garçons et par 20% des filles.
On pose x le nombre total de filles.
On note G l'événement « l'élève est un garçon », F l'événement « l'élève est une fille », S l'événement
« l'élève fait du sport », T l'événement « l'élève fait du théâtre » et D l'événement « l'élève fait du dessin ».
On rassemble les informations précédentes dans le tableau et l'arbre ci-dessous.
|
Garçons
|
Filles
|
Total
|
Sport (S)
|
20-0,1x=6
|
28=0,2 x
|
34
|
Théatre (T)
|
20
|
40
|
60
|
Dessin (D)
|
34
|
72
|
106
|
Total
|
200-x=60
|
x=140
|
200
|
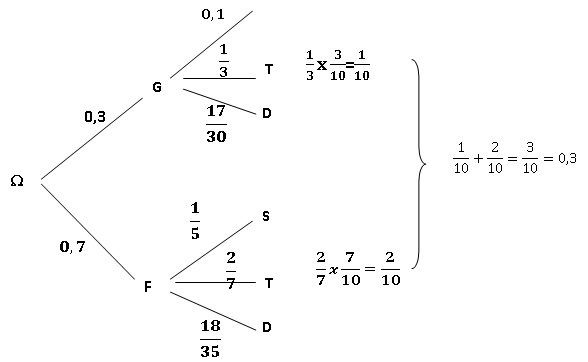
a. La probabilité qu'un garçon fasse du sport est égale à 0,1. Vrai.
b. x=160. Faux.
c. La probabilité qu'un élève fasse du théatre est égale à 0,3. Vrai.
d. PT(F)= 2/5. Faux..40 / 60 = 2 / 3.
.
|
| .
. |
|
|
Exercice 5-2016. Calcul du nombre d'abonnés d'une société.
Le service commercial d'une société possédant plusieurs salles de sport
dans une grande ville a constatéque l'évolution du nombre d'abonnés
était définie de la manière suivante :
• chaque année, la société accueille 400 nouveaux abonnés ;
• chaque année, 40% des abonnements de l'année précédente ne sont pas renouvelés.
En 2010 cette société comptait 1 500 abonnés.
La suite {an ) modélise le nombre d'abonnés pour l'année 2010 + n.
On définit la suite (vn ) par vn = an -1000 .
a) a1 =1300. Vrai.
a0 = 1500 ; a1 = 0,6 x1500 +400=1300.
b) an+1=0,6xan +400. Vrai.
c) La suite (vn) est une suite géométrique de raison q = 0,4. Faux.
v1 = a1-1000 = 300.
a2 = 0,6 x1300 +400=1180 ; v2=1180-1000=180 =0,6 v1.
a3 = 0,6 x1180 +400=1108 ; v2=1108-1000=108 =0,6 v2.
d) an =500x0,6n-1 +1000. Faux.
Cette relation donne a1 = 500+1000=1500, différent de 1180.
Exercice 13- 2016 Probabilités continues.
La durée de vie (exprimée en années) d'un appareil électroménager avant
la première panne est une variable aléatoire X qui suit une loi
exponentielle de paramètre l. > 0.
a) Pour tout réel t strictement positif, p(X supérieur ou égal à t) =1-e-lt. Faux.
Pour tout réel t strictement positif, p(X supérieur à t ) =e-lt.
b) Si la probabilité d'avoir une panne la première année est égale à 0,2, alors l = ln (5/4). Vrai.
p(X inférieur ou égal à 1) = 0,2 = 1-e-l ; 0,8 = e-l ; l = -ln0,8= ln(1/0,8)= ln(5/4).
Soit Y une variable aléatoire suivant la loi normale N (0 ; s2 ) avec s > 0 .
Pour tout u réel, on pose P(u) = P(Y inférieur ou égal à u).
P(u) représente l'aire de la surface hachurée ci-dessous.
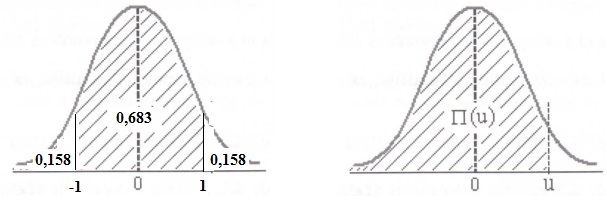
c) P ( 0 <= Y <= s ) > 0 , 4. Faux.
d) P(-s) inférieur ou égal à 0,10. Faux.
Exercice 13-2015. Variables aléatoires réelles : Cours - Calculs
X est une variable aléatoire qui suit la loi exponentielle de paramètre l = 1.
a.Pour tout entier naturel n on a p(X >n) =e-n . Vrai.
b. Pour tout entier naturel n, on a PX>n (X>n+1) = P(X<1). Faux.
Soit Y une variable aléatoire suivant la loi normale N (9 ; s2 ) avec s > 0 .
Soit Z = (Y-9) / s.
c. Z suit la loi normale N(0 ; 1). Vrai.
d. P(7 <= Y <=11)= 2P(0<=Z <=2/s). Vrai.
P(-2 /s <=Z <=2 /s)=1-2(1-P(2/s)) = 2P(2/s) -1.
P(0<=Z <=2/s)=P(2/s)-0,5.
|
|
|
|
14-
2015. Probabilités conditionnelles.
Un acteur est sujet à des trous de mémoire.
S’il relit son texte avant d’entrer en scène, la probabilité qu’il ait
un trou de mémoire pendant la représentation vaut 1/9., tandis que s’il
ne relit pas son texte, cette probabilité vaut 1 /3.
S’il a eu un trou de mémoire au cours d’une représentation, il relit
forcément son texte avant la représentation suivante ; mais s’il n’a
pas eu de trou de mémoire, il ne relit son texte qu’avec une
probabilité de 0,5..
On suppose que l’acteur a relu son texte le soir de la première représentation.
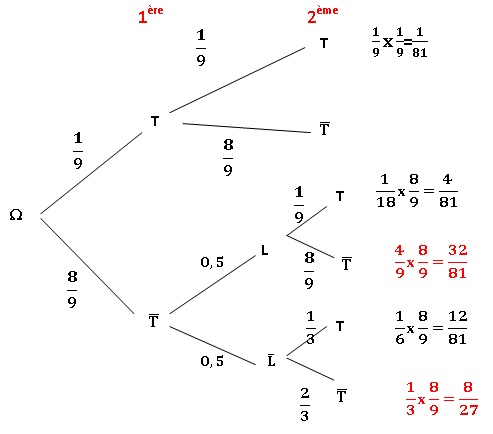
a. La probabilité qu’il ait eu un trou de mémoire lors de la première et de la deuxième représentation est de 1/9. Faux.
Si l'acteur a eu un trou de mémoire lors de la première
représentation, il relit forcément son texte et la
probabilité d'avoir un trou de mémoire lors de la seconde reprsentation
est 1/9.
Si l'acteur n'a pas eu un trou de mémoire lors de la première
représentation, il relit une fois sur deux son texte la fois suivante et la probabilité
d'avoir un trou de mémoire lors de la seconde représentation est 1/9 ou de 1/3..
b. La probabilité qu’il ait eu un trou de mémoire à la deuxième représentation est de 25 / 81. Faux.
c. Sachant qu’il
n’a pas eu de trou de mémoire le soir de la première, la probabilité
qu’il n’en ait pas eu non plus à la deuxième représentation est de 7
/9. Faux.
On note pn (n étant un entier naturel non nul) la
probabilité de l’évènement « l’acteur a eu un trou de mémoire lors de
la n-ième représentation ».
d. Pour tout entier n >1, pn+1 = (2−pn ) / 9. Faux.
Il relit forcément son texte avant la n+1 ième représentation. et la probabilité d'avoir un trou de mémoire est pn /9.
|
|
|
|