Mathématiques,
fonctions, nombres complexes, intégrales,
concours Puissance 11. 2016
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Exercice 1.
Soit f une fonction définie, dérivable et ne s'annulant pas sur
l'intervalle I=[0 ; 4]. On pose Cf la courbe représentative
de f
dans le repère orthonormé g la fonction définie sur [ 0 ; 4 ] pa
r g(x) = 1/f(x).
La tangente T au point A(3 ;2) passe par le point B(2 ;0).
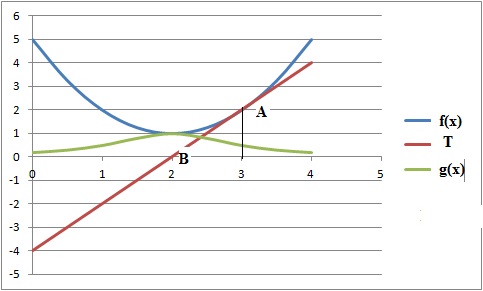
a. f '(2)=1. Faux. b.
f '(3)=f(3). Vrai. c. Une équation de T est y = 2x+2.
Faux .d.
g'(3)=0,5. Faux.
f(x) =ax2+bx+c ; f(0)=5 d'où c =5.
f '(x) = 2ax+b ; f '(2)=0 = 4a+b soit b= -4a.
f(2)=4a+b+5=1 , d'où a=1 ; b=-4.
f(x) =x2-4x+5.
f '(x) = 2x-4.
f(3) = 2 ; f '(3)=2 ; f '(2)=0.
Equation de T : y = f '(3)x+b = 2x+b ; T passe en A(3 ; 2) d'où b = -4.
g(x) = 1/(x2-4x+5) ; on pose u = x2-4x+5
; u' = 2x-4.
g'(x)=-u'/u2 =(-2x+4) / (x2-4x+5)2 ; g'(3)= -2/4= -0,5.
Exercice 2. Logique.
Soit x un réel donné.

Soit f une fonction définie et dérivable sur un intervalle I = [-3 ;7].
c) Si, pour tout x de I , f '(x) > 0 et f (-3) = 1 alors, pour tout x de l , f(x) > 0. Vrai.
La dérivée est positive sur cet intervalle, alors f(x) est strictement croissante sur I.
f(x) est minorée par f(-3)=1, alors, pour tout x de l , f(x) > 0.
d) Si une suite est croissante et admet une limite finie alors elle est nécessairement bornée. Vrai.
Pour qu'une suite soit bornée, il suffit qu'elle le soit à partir d'un certain rang.
Une suite est bornée si elle est majorée et minorée.
Une suite croissante est minorée par son terme initial. Elle est majorée si elle admet une limite finie.
Exercice 6 . calcul de
limites.
Quand x tend vers +oo :
a. la limite de 3x2-4x+7
est égale à -oo. Faux.
Au voisinage de l'infini, 3x2-4x+7
est équivalent à 3x2. Ce dernier tend vers l'infini.
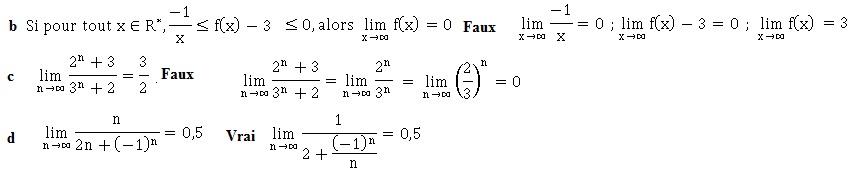
Exercice 7. Notions de
bases sur les complexes.
a : (2i)4
= -16. Faux.
24 x i2 x i2 = 16 x(-1)x(-1) = 16.
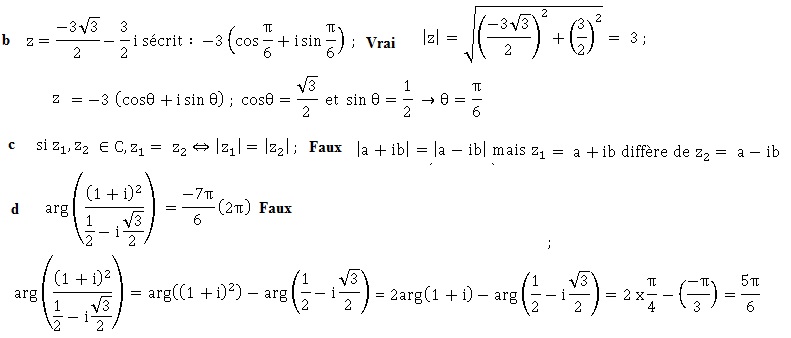
.
Exercice 8. Calcul d'intégrales.
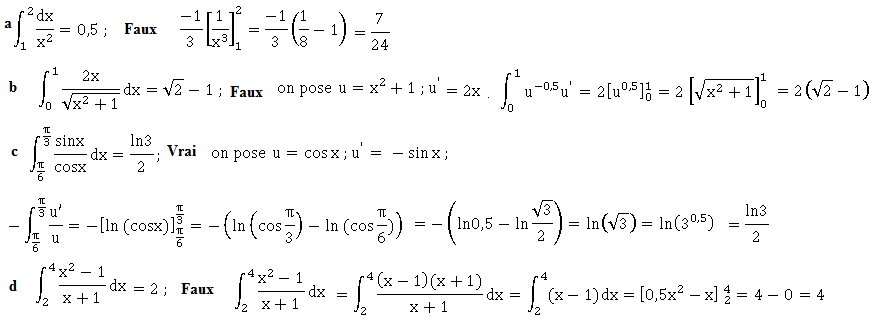
|
| .
. |
|
|
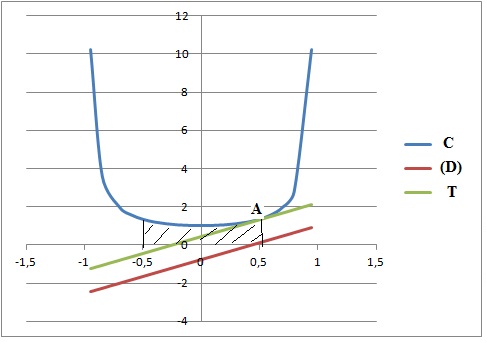
Exercice 9. Etude de fonction.
On considère la fonction/définie sur ] - l ; l [ par
f(x) =1/(1-x2)
On note C sa représentation graphique dans le repère.
a :
La dérivée de f est définie sur ]—1 ; l[ par f '(x) =2x / (1-x2)2.
Vrai.
On pose u = 1-x2 ; u' = -2x ; f '(x) = -u' / u2 =
2x / (1-x2)2.
. b : La tangente à la courbe C au
point A d'abscisse x = 0,5 est parallèle à la droite (D) d'équation 16x
- 9y - 7 = 0. Vrai.
(D) : y = 16/9 x
-7/9.
Coefficient directeur de la tangente T à C en A : f '(0,5) =1/ (1-0,25)2=16/9.
T et (D) ont le même coefficient directeur : ces droites sont
parallèles.
c : La fonction F
définie sur ]-1 ;1[ par F(x) = -0,5 ln((1-x) / (1+x) est une primitive
de f. Vrai.
Dériver F en posant
u =1-x et v = 1+x ; u'=-1 ; v' = 1 ; (u'v-v'u)/v2 =-
((1+x)+1-x)/(1+x)2= -2/(1+x)2;
F '=-0,5*(-2)(1+x) / [(1+x)2(1-x)]
=1 /[(1+x)(1-x)]=1/(1-x2)=f(x).
d : L'aire du domaine (hachurée sur
la figure) compris entre les droites d'équations x = -0,5 ; x =
+0,5,l'axe des abscisses et la courbe C vaut, en unités d'aires du
repère, 0,5 ln(3). Faux.
F(0,5)-F(-0,5)= -0,5 [ln(0,5/1,5)-ln(1,5/0,5)]= -0,5[ln(1/3)-ln3]= ln3.
Exercice 10.
On considère la fonction f définie sur R par f( x ) = e2x -
2ex + 5x + 4.
On définit f ' la dérivée de f et f " la dérivée de f '.
a.
f '(x) = 2e2x-2ex+5 et f"(x) =2ex(2ex-1).
Vrai.
b. 2ex-1
>0 implique x<ln2 et réciproquement. Vrai.
ex>0,5 ; x >ln(0,5) ; x >-ln(2) ; x<ln2.
c : La fonction f ' est croissante
sur [0 ; +oo[. Vrai.
Etude du signe de f "(x) : (2ex-1)
est positif ; 2ex est positif. f "(x) est
positive : donc f '(x) est croissante.
d :
f est décroissante sur [0 ; +oo[. Faux.
f '(0)=5 ; f '(x) est croissante sur [0 ; +oo[. Donc f '(x) est positive et
f(x) est croissante.
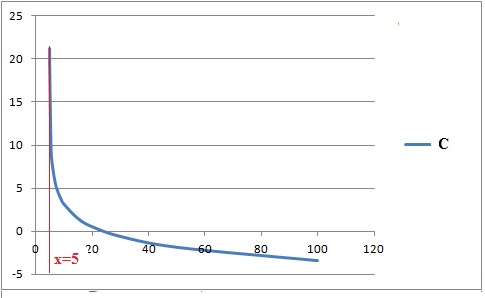
Exercice 11.
On considère la fonction f définie sur I=
]5;+oo[ par f(x) = ln(2x + 1 ) - 3 l n ( x - 5 ) + 5
On note C sa représentation graphique dans un repère orthonormé
a. f '(x)=(4x+13) /
[(2x+1)(5-x)]. Vrai.
f '(x)=2/(2x+1)-3/(x-5) =[2(x-5)-3(2x+1)] / [(2x+1)(x-5)] = -(4x+13) / [(2x+1)(x-5)]=(4x+13) / [(2x+1)(5-x)].
b. C admet la
droite d'équation x = 5 comme asymptote verticale. Vrai.
c. f(x) = ln[e5(2x+1)
/ (x-5)3] Vrai.
f(x) = ln(2x+1) -ln[(x-5)3]+ln(e5).
d. C admet la
droite d'équation y = 5 comme asymptote horizontale en +oo. Faux.
|
|
|
|
14.
Géométrie analytique.
Dans l'espace muni d'un repère orthonormé (0;i,j,k), on donne les plans
(P) et (Q) d'équations cartésiennes respectives
(P) : x + y + 3z = 1 et (Q) : -y + 2z = 4.
(D) est la droite dont une représentation paramétrique est x = -5t +1
; y = 2t ; z = t-1 pour tout / réel.
a) Le plan (Q) est
orthogonal à l'axe des abscisses. Faux.
L'axe des abscisse est dirigé suivant un vecteur de coordonnées (1 ; 0
; 0).
Un vecteur orthogonal au plan Q a pour coordonnées (0 ; -1 ; 2).
b) Les plans (P) et
(Q) sont sécants suivant une droite D. Vrai.
Un vecteur orthogonal au plan P a pour coordonnées (1 ; 1 ; 3).
Un vecteur orthogonal au plan Q a pour coordonnées (0 ; -1 ; 2).
Ces deux vecteurs n'étant pas colinéaires, les plans sont sécants.
c) Une équation
cartésienne de D.
est x + 5z = 5.Vrai.
Les points de D vérifient
x + y + 3z = 1 et -y + 2z = 4 soit par somme : x+5z=5.
d) D est parallèle
à D. Faux.
La droite (D) est dirigée suivant le vecteur de coordonnées (-5 ; 2 ;
1). Ce dernier n'est pas colinéaire au vecteur directeur de la droite D.
15. Nombres complexes et
géométrie.
Le plan complexe est muni d'un repère orthonormé.
On désigne par A, B , C et D les pointsd'affixes respectives : zA
= 2-3i, zB =i, zc =6-i et zD= -2 + 5i.

x ety désignent deux nombres réels, on note f ia fonction qui, à tout
point M d'affixe z = x + iy distinct de i associe le point M'
d'affixe z'.
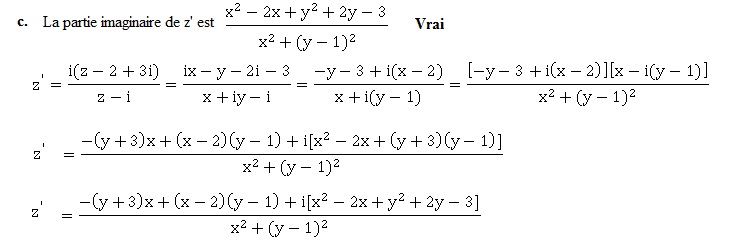
d. L'ensemble y des points M d'affixe z tels que z' soit un réel est
une droite. Faux.
La partie imaginaire de z' doit être nulle.
x2+y2-2x-2y-3=0 ; (x-1)2 +(y+1)2=5,
équation d'un cercle.
|
|
|
|