Mathématiques,
fonctions, nombres complexes, intégrales,
concours Puissance 11. 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Exercice 1. Etude de fonction.
Soit f une fonction dérivable sur R de courbe représentative G dont lafonction dérivée f ′ a pour représentation
graphique la courbe suivante. On admet que : f '(x) = 2 x si x est inférieur ou égal à 1 et f '(x) = 1/x+1 si x >1.
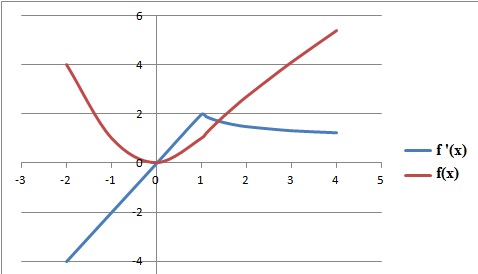
a. La courbe (G) admet une asymptote horizontale en +oo. Faux.
b. Pour tout x ∈]−∞; 1], f (x) = x2. Faux.
f (x) = x2+ constante.
On suppose dans le c. et d. que (G) passe par (1 ; 1).
c. Pour tout x réel, f(x) est positive ou nulle. Vrai.
d. f(2) = ln2 +2. Vrai.
Pour x >1 : f(x) = lnx + x + constante ; f(1,0001) ~1, la constante d'intégration est nulle.
Exercice 2 . Fonction définie par deux paramètres.
Soit a et b deux réels strictement positifs fixés et f la fonction définie sur I = [−a ; a] par f (x) =b / a (a2-x2)½.
de courbe représentative (C).
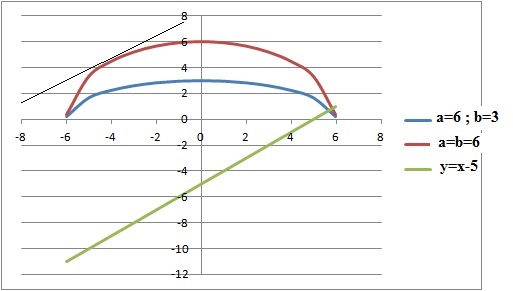
a. Pour tout x ∈ I , f ′(x) =0,5 b /(a2-x2)½. Faux.
On pose u = a2-x2 ; u' = -2x ; f '(x) =b/a [ 0,5u' u-1/2]= - bx/a (a2-x2)-1/2.
b. Si a = 6 et b = 3 alors pour tout x ∈ I , f (x) est supérieure ou égale à 3. Faux.
La dérivée s'annule pour x = 0 ; (a2-x2)-1/2étant positif, a et b étant positif, le signe de f '(x) est celui de -x.
f '(x) est positive pour x négatif : f(x) est strictement croissante sur ]-6 ; 0 [.
f '(x) est négative pour x positif ; f(x) est strictement décroissante sur ]0 ; +6[.
f(x) passe par un maximum égale à b=3.
c. Si a = b = 1, alors l’équation f (x) =2½ admet deux solutions sur I .Faux.
f(x) passe par un maximum égale à b=1.
d. Si a = b alors (C) admet deux tangentes parallèles à la droite (D) d’équation y = x −5. Faux.
f '(x) = - x (a2-x2)-1/2= 1 ; -x=(a2-x2)1/2 ; x doit être négatif. x= -a / 2½.
Exercice 3. Bases de la géométrie.
Les questions suivantes sont indépendantes.
a. Le plan est muni d’un repère orthonormé. Si la droite (D) a pour équation paramétrique
x=t ; y=1+t ; z=2+t, avec t réel.
Un vecteur directeur de (D) a pour coordonnées (1 ; 1 ; 1). Vrai.
b. Soit a > 0. Si ABC est un triangle équilatéral direct de côté a, alors :
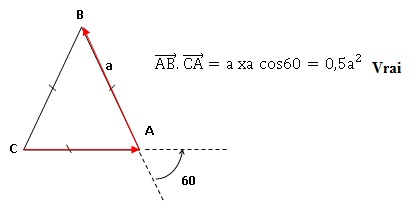
.
Pour le c. et d., on suppose que le plan complexe est muni d’un repère orthonormé direct
c. Le nombre (1+i)4 est un nombre réel négatif. Vrai.
(1+i)2 (1+i)2 =( 1+i2+2i)( 1+i2+2i)=4i2= -4.
d. L’ensemble des points M d’affixe z telle que |z +4−3i| = 5 est un cercle passant par l’origine du repère. Vrai.
x et y réels : z=x+iy ; z+4-3i = (x+4) +i(y-3).
|z +4−3i|= [(x+4)2 +(y-3)2]½=5 ; (x+4)2 +(y-3)2=25.
C'est l'équation d'un cercle centré sur le point (-4 ; +3), de rayon R=5.. Ce cercle passe par l'origine du repère.
.
Exercice 4. Logique.
Agnan, Clotaire, Eudes, Geoffroy et Rufus ne s’entendent pas tous très bien. Pour la fête d’anniversaire qu’organisait le petit Nicolas, ils avaient prévenu :
• Clotaire refuserait de venir si Rufus était présent.
• Eudes ne viendrait que s’il était accompagné d’Agnan ou de Rufus.
• Quant à Geoffroy et Agnan, ils n’iraient nulle part l’un sans l’autre.
a. Si Clotaire n’est pas venu à la fête, alors Rufus était présent. Faux.
Clotaire pouvait être malade, ou avoir un autre rendez-vous.
b. Si Rufus était absent, alors Clotaire est venu à la fête. Faux.
c. Si Agnan est venu, alors Geoffroy et Eudes aussi.Vrai.
d. Si Eudes et Clotaire sont venus, alors Geoffroy était lui aussi présent. Faux.
|
| .
. |
|
|
Exercice 5. Petite démonstration.
Soit f la fonction définie sur R- {0,5 } par f(x) = x2 /(2x-1) de courbe représentative C et I=]0,5 ; +oo[
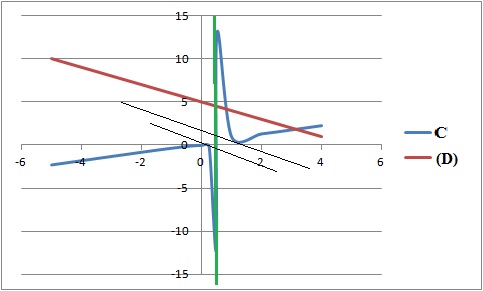
a :
Pour tout réel x appartenant à R- {0,5 }, f '(x) =2x(1-x) / (1-2x)2. Faux.
On pose u = x2 et v = 2x-1 ; u' = 2x ; v' = 2 ; f '(x) = (u'v-v'u) / v2 =[
2x(2x-1)-2x2] / (2x-1)2.
f ' (x) = (2x2-2x) / (2x-1)2 = 2x(x-1) / (2x-1)2.
. b : La courbe admet deux tangentes parallèle à la droite (D) d'équation y = -x+5. Vrai.
2x(x-1) / (2x-1)2 = -1 ; 2x(x-1) = - (2x-1)2 ; 2x2-2x = -4x2-1+4x ;
6x2-6x+1 = 0 ; D = 36-24 = 12, il existe donc deux solutions.
c : Si x appartient à I, la fonction k(x) = ln(f(x) admet comme dérivée k'(x) = 2 /x -2 /(2x-1). Vrai.
k(x) = ln(x2) -ln(2x-1) = 2 ln(x) -ln(2x-1) ; k'(x) = 2 / x -2 /(2x-1).
d : Pour tout n entier, on définit la suite (un) par u0=3 ; un+1 = u2n / (2 un-1)
Afin d’étudier le sens de variation de la suite (un) on effectue le raisonnement suivant ::
« Pour tout n entier, on souhaite démontrer la relation « un+1 −un >0 ».
Si x appartient à I , alors f ′(x) > 0 et la fonction f est strictement croissante sur I .
Supposons que la relation soit vraie à un certain rang k , c’est-à-dire uk+1−uk > 0.
Par définition de la suite (un) nous avons uk+2 = f (uk+1) et uk+1 = f (uk ) avec f strictement croissante sur I ; donc si uk+1 > uk alors nous pouvons en déduire que
uk+2 = f (uk+1) > uk+1 = f (uk ) soit uk+2 > uk+1 ce qui nous permet de conclure que la relation est vraie au rang k +1.
Conclusion : la relation est héréditaire et, comme la fonction f est
strictement croissante sur I , nous pouvons en déduire que la suite (un)n>0 est strictement croissante».
Ce raisonnement est correct. Faux.
f n'est pas strictement croissante sur I. La condition initiale (u1-u0 = 9/5-3 est négatif) est fausse.
Exercice 6. Calculs de limites.
a.
La limite de e1/x est égale à zéro si x tend vers l'infini. Faux.
1/x tend vers zéro au voisinage de l'infini et e0 =1.
b. La limite de (1-ex) / x est égale à 1 quand x tend vers zéro. Faux.
Au voisinage de zéro ex est équivalent à 1+x+x2/2 ; (1-ex) / x est donc équivalent à -1-x/2.
La limite de (1-ex) / x est égale à -1 quand x tend vers zéro.
c : Soit f la fonction définie sur ]0 ; +oo[ par f (x) =(ex+1) /(ex-x-1). La courbe (C) représentative
de la fonction f admet l’axe des abscisses comme asymptote horizontale. Faux.
Par croissance comparée, ex-x est équivalent à ex et f(x) est équivalent à ex /ex =1 au voisinage de l'infini.
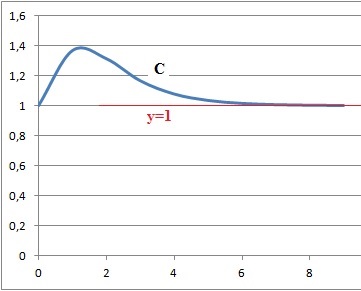
d : Pour tout n entier, la suite (un) définie par un =(sin(n)−2n) /(n +1) converge vers 0. Faux.
sin (n) est négligeable devant -2n quand n devient grand. un tend vers -2n / (n+1) = -2 quand n tend vers l'infini.
Exercice 7. Calcul intégral.
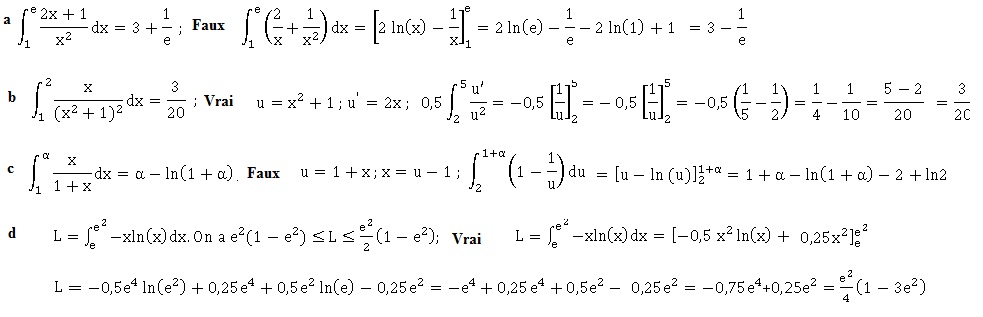
|
|
|
|
8. Fonction exponentielle
Soit F1 et g les fonctions définies sur R respectivement par F1(x) = e−x −2x et g (x)= e−x (x +1) / (e−x +2).
On désigne par (C) la courbe représentative de la fonction F1 et par (xn) la suite définie, pour tout n entier, par x0 = 1 et xn+1 = g (xn).
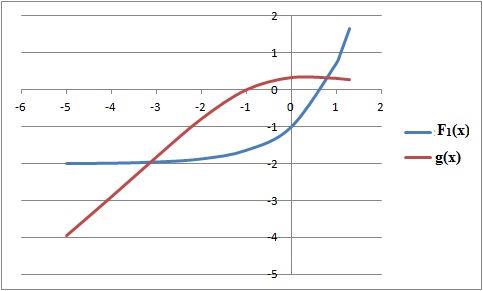
a) L’équation F1(x) = 0 admet une unique solution α avec 0 < α < 1. Vrai.
Dans les questions b., c. et d., on admet la convergence de la suite (xn).
b) La limite de xn est égale à a quand x tend vers l'infini. Faux.
g (x)= (x +1) / (1+2ex). g() est équivalent à x / (2ex) quand x tend vers l'infini. Par croissance comparée, g(x) tend vers zéro quand x tend vers l'infini.
c) Si a est réel, alors la tangente à (C) en x = a coupe l’axe des abscisses en un point d’abscisse g (a). Vrai.
F '1(x) = -e-x-2 ; coefficient directeur de la tangente à C au point d'abscisse x=a : -e-a-2.
La tangente passe par le point A( a ; e-a-2a) ;
Equation de cette tangente : e-a-2a = (-e-a-2)a+b ; b = (1+a)e-a ; y =(-e-a-2)x+ (1+a)e-a ;
La tangente coupe l'axe des abscisses au point de coordonnées ( (1+a)e-a / (e-a+2) ; 0).
9. Fonction exponentielle et logarithme.
Soit f la fonction définie sur ]0 ; +oo[ par f (x) =ln(e2x −1) / ex , g la fonction définie sur ]1 ; +oo[ par g (x) = 2x−(x−1)×ln(x−1) et F la fonction définie sur ]1 ; +∞[ par f(x)=ln(x2 −1) / x.
.
a. g'(x) = 1+ln(1 / (x-1)). Faux.
On pose u = (x-1); v = ln(x-1) ; u'=1 ; v' = 1/(x-1) ; u'v+v'u = ln(x-1) +1 ; g'(x) = 2-(ln(x-1)+1).
b. f '(x) = g(x2) / x2. Faux.
On pose u = ln(x2 −1) ; v = x ; u' = 2x/(x2 −1) ; v' = 1 ; (u'v-v'u) / v2 =[2x2 /(x2 −1) - ln(x2 −1) ] / x2 .
c. g admet un minimum en x = e+1. Faux.
g'(x) = 0 pour x = e+1.
g'(x) est négative pour x > e+1 ; g(x) est décroissante pour x > e+1.

|
|
|
|
Exercice 10. Suite et trigonométrie.
Soit (un) la suite définie, pour tout n entier, par un = (−1)n +2×sin(np/4).
a. Pour tout entier naturel n, on a : un+8 > un. Faux.
un+8 = (−1)n+8 +2×sin((n+8)p/4) =(−1)n(−1)8+2×sin((np/4+2p)=(−1)n +2×sin(np/4) = un.
b. Pour tout entier naturel n, un appartient à [-3 ; +3]. Vrai.
Pour n impair : (−1)n = -1 ; valeur minimale de 2×sin(np/4) = -2½. Valeur minimale de un ; -1-2½~ -2,14.
Pour n pair : (−1)n = +1 ; valeur maximale de 2×sin(np/4) = 2. Valeur maximale de un : 3.
c. La suite (un) est monotone. Faux.
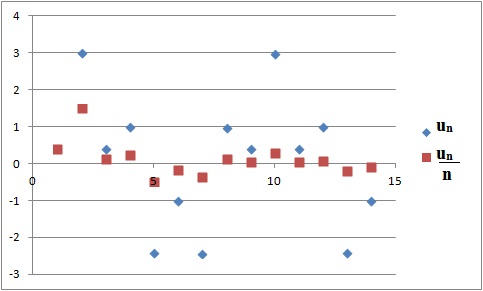
d. Quand n tend vers l'infini, la limite de un / n est nulle. Vrai.
Exercice 11. Suite de nombres complexes.
On se place dans le plan complexe muni d’un repère orthonormé direct et on considère la suite (zn) de nombres complexes définie, pour tout n entier, par :
z0 = 2 ; zn+1 =0,5(1+i)zn.
On pose An le point d’affixe zn et on définit, pour tout n entier, la suite (un) par un = |zn|.
a. La suite (un) est géométrique. Vrai.
Démonstration par récurrence :
Initialisation : z1 =0,5(1+i) x 2 =1+i ; u1 = (12+12)½ = 2½ ; u1 = 2½ /2 u0.
Hérédité : la propriété est supposée vraie au rang p : up+1 = 2½ /2 up.
zp+2 =0,5(1+i)zp+1 ; up+2 =0,5|1+i| up+1 =2½ /2 up+1. La propriété est vraie au rang p+1.
Conclusion : La propriété étant vraie au rang 1 et héréditaire, alors la suite est géométrique.
b. Pour tout entier naturel n,( zn+1 −zn ) / zn+1 = i. Vrai.
1- zn / zn+1 =1-2/(1+i) = (1+i-2) / (1+i)=(i-1) / (1+i)=(i-1)(1-i) / 2 =i.
c. À partir du rang n = 4, le point An appartient au disque de centre O et de rayon R =0,5. Faux.
zn+1 = 2½ /2 exp(ip/4) zn = (2½ /2)n z0 exp(in p/4). Le module de zn n'est pas constant.
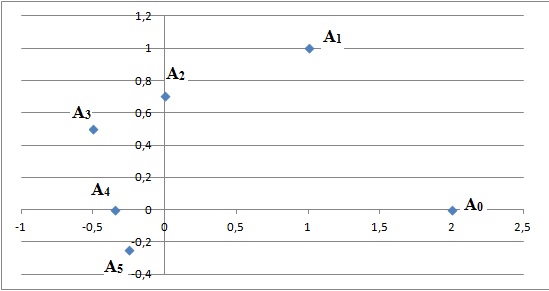
d. Pour tout entier naturel n, le triangle OAn An+1 est isocèle et rectangle. Faux.
Exercice 12. Géométrie et complexes.
Le plan complexe est muni d’un repère orthonormé direct.
On définit A et B deux points d’affixes respectives zA = 1 et zB = 2i et T la transformation complexe du plan qui, à tout point M d’affixe z non nulle, associe le point
M′ d’affixe z′ =(z −2i) / z.
a. L’image du point d’affixe exp(ip/4) par la transformation T est le point d’affixe 1+2exp(-ip/4). Faux.
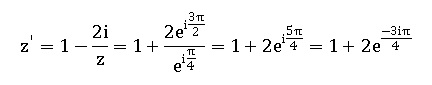
b. L’ensemble des points M du plan complexe tels que OM′ = 1 représente la médiatrice du segment [OB]. Faux.
z' = x+iy ; x2+y2=1. M' appartient au cercle centré en O, de rayon R=1.
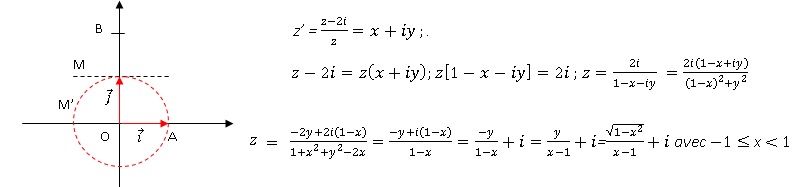
c. M′ appartient au
cercle de centre A et de rayon 1 si et seulement si le point M
appartient au cercle de centre O et de rayon R = 2. Faux.
Si M' est tel que : (x-1)2+y2 = 1, alors :
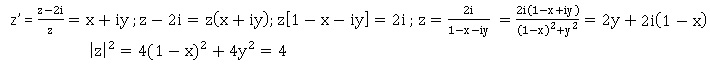
M appartient au cercle de centre O et de rayon R=2.
Réciproque : si M appartient au cercle de centre O et de rayon R = 2, alors z = x+iy avec x2+y2 = 4.
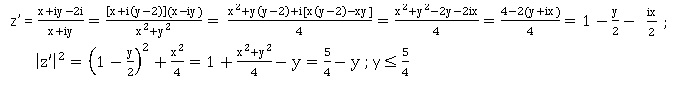
d. z′ est un nombre complexe imaginaire pur si et seulement si le point M appartient au cercle de diamètre [OB]. Vrai.
Si M appartient au cercle de diamètre [OB] : z= x+iy avec x2+(y-1)2 = 1 soit x2 +y2 =2y.
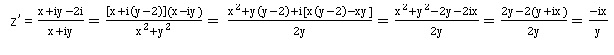
Réciproque : si z' =a i avec a réel, alors :
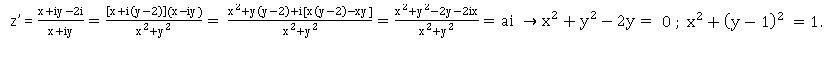 : :
|
|