Mathématiques,
fonctions, nombres complexes, intégrales,
concours Puissance 11. 2012
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Exercice 1.
Soit la fonction f définie sur R* par f(x) =(1-x)(1-ex) / x.
a. Quand x tend vers zéro, f(x) tend vers zéro. Faux.
Au voisinage de zéro, f(x) est équivalente à (1-ex) / x.
1-ex équivalent à 1 -(1+x+x2/2) =-x-x2/2.
(1-ex) / x est équivalent à -1.
b.
Quand x tend vers moins l'infini, la limite de f(x) est 1. Faux.
Au voisinage de -oo, le terme ex est nul ; f(x) est équivalente à -x / x =-1.
c. On appelle g la fonction définie sur R par: g(x) = f (x) si x diffère de zéro et g(0) = –1.
La fonction g est continue sur R. Vrai.
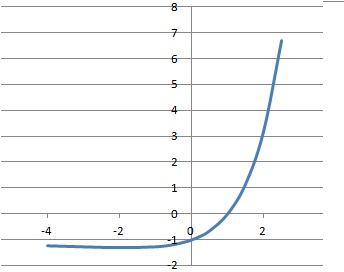
d. Quand x tend vers plus l'infini, la limite de (n-1)(1-exp(1/n)) est égale à -1. Vrai.
On pose x = 1/n ; au voisinage de zéro, 1-ex équivalent à 1 -(1+x+x2/2) =-x-x2/2.
1/x-1 est équivalent à 1/x ; (n-1)(1-exp(1/n)) est équivalent à -1.
Exercice 2 .
Soit f la fonction définie par f (x) = ln(e2x – 2ex + 1).
a. L'ensemble de définition de f est R. Faux.
e2x – 2ex + 1 = (ex-1)2, toujours positif ou nul ( si x = 0).
f(x) n'est pas définie en 0.
b. On a: f (x) < 0 si et seulement si x < 0. Faux.
f(0,1) =2 ln(e0,1-1)= -4,5 .
c. Pour tout x de R*, on peut écrire f (x) = 2ln(ex – 1). Faux.
f (x) = 2ln |ex – 1|
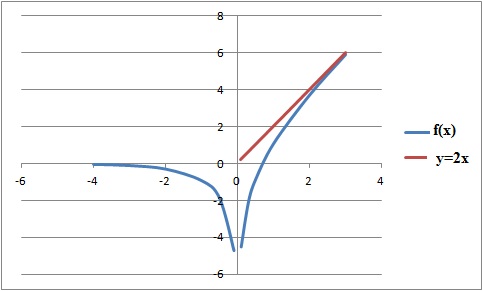
d.
La courbe représentant f dans un repère orthonormal du plan possède
pour asymptotes les axes du repère et la droite d'équation y = 2x. Vrai.
Exercice 3.
Pour tout n entier naturel non nul, on définit la fonction fn sur ]0, +oo[ par: fn(x) = ln(x) + 2ln(n) – nx et on appelle Cn la courbe représentant fn dans un repère orthonormal du plan.
a. Pour tout n entier naturel non nul et pour tout réel positif non nul , on a: fn'(x) =(n+2x-xn2) / (nx). Faux.
fn'(x) =1/x -n =(1-nx) / (x).
b. On fixe n. fn est décroissante sur ]1, +oo[.. Vrai.
Sur cet intervalle, x est positif et 1-nx est négatif ; f 'n(x) est négative.
c. Pour tout n entier naturel non nul, on appelle Mn l'extremum de la courbe Cn. On note (xn, yn) les coordonnées de Mn.
La suite (xn)n est décroissante et la suite (yn)n est croissante.. Vrai.
(xn)n = 1 / n, suite décroissante.
yn= ln(1/n)+2ln(n)-1=ln(n)-1 ; (yn)n , suite croissante.
d. On fixe n dans N*. La fonction Fn définie par: Fn(x) = xln( x) – x + 2xln( n) –nx2/2 est la primitive de fn sur ]0, +oo[ qui tend vers 0 quand x tend vers 0.. Vrai.
F'n(x) =ln(x)+1+1+2ln(n)-nx=ln(x)+2ln(n)-nx=f(x).
Fn(x) est équivalent à x ln(x) au voisnage de zéro.
.
Exercice 4.
On considère la représentation graphique suivante d'une fonction f.
On appelle C la courbe représentant f et on suppose que la droite
d'équation y = 1 est asymptote à C aux voisinages de +oo et de –oo.
On appelle f ' la dérivée de f lorsqu'elle existe.
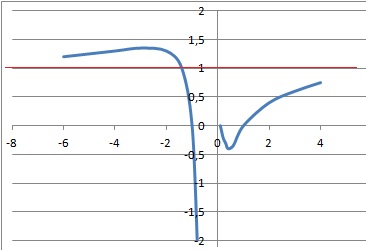
a. La limite de f (x) quand x tend vers 0 existe. Faux.
La fonction n'est pas définie pour x appartenant à 0+ ; 0,1.
b. Quand x0 tend vers 0 par valeurs positives, 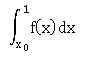 représente l'aire, en unités d’aire, de la représente l'aire, en unités d’aire, de la
surface comprise entre la courbe et l'axe des abscisses.. Faux.
c. La limite de f '(x) quand x tend vers +oo est égale à 1.. Faux.
La tangente à C se rapproche de l'horizontale, f '(x) tend vers zéro quand x tend vers +oo.
d. Entre 0 et 4, la fonction f ' est décroissante, puis croissante, puis à nouveau décroissante.. Vrai.
La pente de la tangente à la courbe diminue de 0 à 0,4 , s'annule, puis croît de 0,4 à 1, pour décroître ensuite.
|
| .
. |
|
|
Exercice 5.

Exercice 6. .
a. On cherche l'ensemble de définition de la fonction f définie par f (x) = ln [(15+2x-x2) / (x2+10x+21)]
On tient pour cela le raisonnement suivant:
«f est définie si et seulement si on a (15+2x-x2) / (x2+10x+21) >0.
Or 15 + 2x – x2 = (3 + x)(5 – x) et x2 + 10x + 21 = (x + 3)(x + 7).
Il faut donc et il suffit d'avoir (5-x) /(x+7) >0. et x différent de -3.
soit x appartenant à ]–7, 5[.
Conclusion: l'ensemble de définition cherché est ]–7, 5[.»
Ce raisonnement est exact. Faux.
b. On considère la fonction f, définie sur I = R+* par f (x) = x2 – xln(x2).
On cherche à montrer que f est croissante sur I. On tient pour cela le raisonnement suivant:
«f est dérivable sur I. Pour x appartenant à I, on a f '(x) = 2(x – 1 – ln x).
Or la représentation graphique de la fonction ln est située en dessous
de ses tangentes en tout point. En particulier elle est située en
dessous de sa tangente au point d'abscisse 1 qui est la droite
d'équation y = x – 1.
On en déduit que, quel que soit x de I, on a: ln x < x – 1.
Il s'ensuit que l'on a: f '(x) > 0.
Ceci étant vrai pour tout x de I, on en déduit que f est croissante sur I.»
Ce raisonnement est exact. Vrai.
c : On considère quatre points A, B, C et D de l'espace, deux à deux distincts.
On appelle I le milieu de [AB] et, pour tout m réel, on appelle Gm le barycentre de {(A, 1), (B, 1),
(C, m – 2), (D, m)}.
On cherche à montrer que, quel que soit m réel, Gm est situé dans le plan (ICD). On tient pour cela le raisonnement suivant:
«I est le milieu de [AB], donc I est le barycentre de {(A, 1), (B, 1)}.
Quel que soit m réel, et par associativité du barycentre, Gm est alors le barycentre de {(I, 2), (C, m – 2), (D, m)}.
On en déduit que Gm appartient au plan (ICD).»
Il faudrait préciser que les points ne sont pas alignés.
Ce raisonnement est exact. Faux.
d : On considère la fonction f, définie sur ]0, +oo[ par f (x) = e–x – ln( x) – x.
On considère la rédaction suivante qui donne le sens de variation de f.
«f (x) est dérivable sur ]0, +oo[ et, pour x appartenant à ]0, +oo[, on a f '(x) = –e–x –1/x-1.
f '(x) est la somme de trois nombres négatifs, donc on a: f '(x) < 0.
Il s'ensuit que f (x) est strictement décroissante sur ]0, +oo[.»
Cette rédaction est rigoureuse. Faux.
Exercice 7.
On considère l'équation différentielle [E]: y' + 2y = 4.
a.Soit z une fonction dérivable sur R.
z est solution de [E] si et seulement si z – 2 est solution de l'équation y' + 2y = 0. Vrai.
La dérivée de z-2 est z' ; z étant solution de (E), z'+2z=4.
z-2 est solution de y'+2y=0 : z' +2(z-2) = 0 est vérifiée.
b. L'application f, définie par f (x) = 2(1 – e2(1–x)) est une solution de [E].
f 'x) = 4e2(1–x) ; repport dans [E] :
4e2(1–x)+4(1 – e2(1–x)) = 4 est vérifiée quel que soit x.
c. L'application g, définie par g(x) = 2 – e2x+4 est la solution de [E] vérifiant g(–2) = 1. Faux.
g'(x) = -4e2x+4 ; repport dans [E] : -4e2x+4 +4-2e2x+4 diffère de 4.
d. L'application h, définie par h(x) = 2 +[exp(-x-1)]2 est la solution de [E] vérifiant h'(–1) = –2. Vrai.
On pose u = exp(-x-1) ; u' = -exp(-x-1) ; h'(x) = 2uu' = -2[exp(-x-1)]2 ;
Repport dans [E] : -2[exp(-x-1)]2 +4+[exp(-x-1)]2 =4 est vérifié quel que soit x.
h'(-1) = -2(e0)2 = -2.
|
|
|
|
Exercice 8.
On étudie l'évolution de deux fourmilières A et B.
Chaque mois, 20% des fourmis de A passent en B et 30% des fourmis de B passent en A.
Au bout d'un nombre de mois égal à n, on note un et vn le nombre total (en milliers de fourmis) de fourmis présentes respectivement dans les fourmilières A et B.
On a dénombré que, initialement, on avait u0 = 320 et v0 = 180.
a. Pour tout n entier naturel, on a : un+1 = 0,8 un+0,3 vn ; vn+1 = 0,2 un+0,7 vn . Vrai.
b. La suite s = u + v est une suite constante. Vrai.
un+1 +vn+1 =un+vn = constante =u0+v0=500.
c. La suite t = –2u + 3v est géométrique de raison 0,5 et vérifie, pour tout n de N : tn = -100 /2n. Vrai.
tn+1= -2un+1 +3vn+1 = -1,6 un-0,6 vn + 0,6 un+2,1 vn = -un+1,5 vn=0,5(-2un+3vn)=0,5 tn.
t0= -2u0+3v0=-2 x320+3 x180 = -100 ; tn = -100 /2n.
d. Quel que soit n de N, on a: vn = 200 – 20 / 2n. Vrai.
tn = -2un +3vn = -100 /2n.
un +vn =500 ; 5vn-1000 =-100 /2n ; 5vn =1000 -100 /2n ; puis diviser par 5.
Exercice 9.
Soit u une suite numérique dont aucun terme n'est nul.
On définit la suite v par: vn =1+1/un.
a) Si u est convergente, alors v est convergente. Faux.
Si u converge vers zéro, v diverge vers l'infini.
b) Si u est minorée par 1, alors v est majorée par 2. Vrai.
c) Si u est majorée par 0,5, alors v est minorée par 3. Faux.
Par exemple si u =-1, alors v = 0.
d) On suppose ici que u est définie par: u0 > 0 et un+1 =un /(un+2)
Alors v est une suite géométrique. Vrai.
vn+1 =1+1/un+1 = 1 +(un+2) / un = 2(un+1)/un= 2(1+1/un)=2 vn.
|
|
|
|
Exercice 10.
On considère les suites u et v définies par : un = 1 +1 /1! +1 / 2! +...+1/n! et vn = un +1 /(n xn!).
a. Quand n tend vers l'infini, un tend vers zéro. Faux.
Seul le terme 1/n! tend vers zéro.
b. La suite v est croissante.
Faux.
u1 = 2 ; u2 =2,5 ; v1 =3 ; v2 =2,75.
c. Les suites u et v sont adjacentes. Vrai.
u et croissante ; v est décroissante ; la différence u-v converge vers zéro.
d. Quel que soit n de N*, on a : 2 < un <un+1 < vn+1 <vn <3. Vrai.
Exercice 11.
Dans le plan complexe muni d'un repère orthonormal, on appelle A le point dont l'affixe est –i.
Pour tout point M distinct de A, d'affixe z = x + iy (écriture
algébrique), on associe le point M' d'affixe z' = x' + iy' (écriture
algébrique) telle que :
z' = (x-iy) / (x-i(1+y)).
a. x'=(x2+y2+y) / (x2+(y+1)2). Vrai.
z' = (x-iy)(x+i(y+1) / (x2+y+1)2) ; z' = (x2+y2+y+ix) / (x2+(y+1)2).
b. Le conjugué de z' est égal à z / (z+i). Vrai.
(x+iy) /(x+i(y+1))=(x+iy)(x-i(y+1)) / (x2+y+1)2) = (x2+y2+y-ix) / (x2+(y+1)2).
c.L'ensemble des points M tels que z' = conjugué de z' est l'axe des ordonnées privé du point A. Vrai.
Im(z') =0 soit x = 0.
d. M' appartient au cercle de centre O et de rayon 1 si et seulement si M appartient à la médiatrice de [OA].. Vrai.
Equation de la médiatrice de [OA]. y =-0,5 ; afixe de M : z = x-0,5 i.
z' = (x2+y2+y+ix) / (x2+(y+1)2) avec y = -0,5.
z' = (x2-0,25+ix) / (x2+0,25) ; |z'|2=((x2-0,25)2 +x2) / (x2+0,25)2=1.
Exercice 12.
Soit a un nombre complexe non réel.
Dans le plan complexe, on considère le point A d'affixe a, le point B
d'affixe ia, le point C d'affixe –a et le point D dont l'affixe est le
conjugué de a.
a. C est l'image de A par la rotation de centre B et d'angle p/2. Faux.
A(x ; y ) ; B( -y ; x) ; C(-x ; -y) ; D(x ; -y)
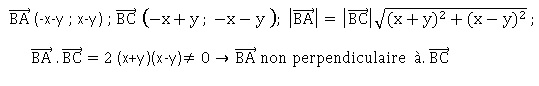
b. L'angle (DA; DC) est égal à p/2 +kp où k appartient à Z. Vrai.
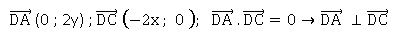
c. L'ensemble des points M d'affixe z telle que |z – a| = |z + a| est la droite (AC)..
Faux.
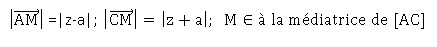
d. Les points A, B, C et D sont situés sur un même cercle. Vrai.
A et C sont symétriques par rapport à l'origine O du repère ; ils sont situés sur le cercle de centre O et de rayon |a| = (x2+y2)½.
OB = (x2 +(-y)2)½ ; OD = (x2 +(-y)2)½ .
Exercice 13.
Le plan complexe est rapporté à un repère orthonormal.

d. Il existe nde N* tel que le point Mn d'affixe Zn appartienne à l'axe des abscisses. Vrai.
Exercice 14.
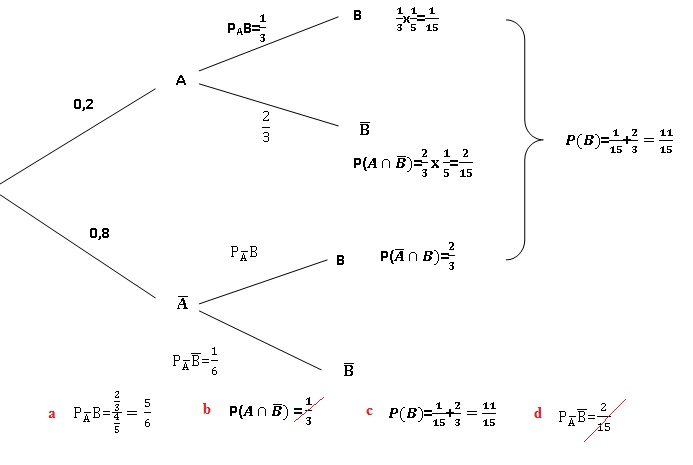
Le code d'entrée dans un immeuble est composé de quatre chiffres.
a. Il y a 9999 codes différents. Faux.
0000 à 9999 soit 10000 codes différents.
b.
Pour éviter les erreurs de saisie, certains occupants demandent qu'un
même chiffre ne puisse pas être répété deux fois consécutivement.
Il y a alors 7290 codes différents possibles.. Vrai.
c. Certains occupants préféreraient que les 4 chiffres soient tous différents.
Il y aurait alors C104 codes différents possibles..
Faux.
d. Comme cet immeuble est situé à Paris, certains occupants souhaitent que le code choisi contienne le nombre «75».
Il y aurait alors 168 codes différents possibles. Faux.
16. Géométrie dans l'espace.
Dans
l'espace rapporté à un repère orthonormal, on considère les plans P et
Q d'équations respectives: P: y = x + 2 et Q: z = 3 – 2y.
On appelle (D) la droite d'intersection de P avec Q.
a) La droite D accepte pour vecteur directeur, le vecteur de coordonnées (1, 1, –2). Vrai.
Les points de la droite (D) vérifient : y = x+2 ; z = 3-2(x+2) = -2x-1.
Equations paramétriques de (D) : x = t ; y = t+2 ; z = -2t-1 avec t réel.
Coordonnées du vecteur directeur de cette droite ( 1 ; 1 ; -2).
b) La droite D passe par le point A(–1, 1, 1)..Vrai.
Les coordonnées du point A doivent vérifier les équations paramétriques de (D) :
x=t=-1 ; y = -1+2 = 1 =yA ; z=2-1=1=zA.
c) Une équation du plan contenant la droite D et passant par O est: 3x + y + 2z = 0. Vrai.
Coordonnées d'un vecteur normal à ce plan : (3 ; 1 ; 2).
Coordonnées du vecteur directeur de la droite (D) ( 1 ; 1 ; -2).
Le produit scalaire de ces deux vecteurs est nul.
d) La droite D coupe l'axe des ordonnées. Faux.
.
|
|