Mathématiques, concours Ecole de santé des armées ( ESA) 2015

Mathématiques, concours Ecole de santé des armées ( ESA) 2015

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Exercice 1.
QCM 1 :
La limite quand n tend vers +oo:
A. de 12n² −7n −5 vaut −5. Faux.
n²(12 -7 / n -5 /n²).
Au voisinage de l'infini : -7 /n et -5 /n² tendent vers zéro.
12 -7 / n -5 /n² tend vers 12.
Par produit de limites, 12n² tend vers l'infini.
B. de 12n² −7n −5 vaut 0. Faux.

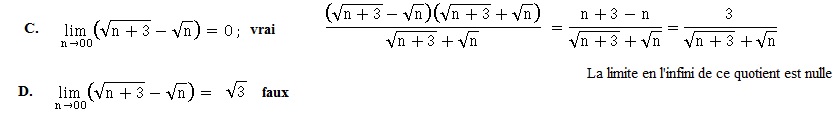
QCM 2 :
La suite (u_n) définie pour tout n dans N par u_n = 3×2⁻ⁿ est :
A. croissante.
u_n = 3 / 2ⁿ ; suite positive décroissante vers zéro.
B. convergente vers 3
C. convergente vers 0. Vrai.
D. arithmétique. Faux, suite géométrique de raison 1/2.

QCM 3 :
Le nombre A = e³(e⁻²)⁵ e peut également s’écrire :
A. e⁻¹³.
e⁴ x e^-10 = e^-6.
B. e⁷
C. e⁻⁶ vrai.
D. e⁻³⁰.

QCM 4.L’équation : exp(x²−2x) =1 / e admet, dans R, pour ensemble de solutions :
A. aucune solution;
B. {1} vrai.
C. {1 ; 2}
D. {0 ; 2}
x²−2x = -1 ; x²−2x +1=0 ; (x-1)² = 0 ; x = 1.

QCM 5 :
L’inéquation : exp(1−x /5) >1 admet, dans R, pour ensemble de solutions :
A. ]−∞; 5[ vrai.
B. ]0 ; 5[
C. ]−∞; 0[
D. ]1/5 ; +∞[
Par croissance de la fonction logarithme népérien :
1-x / 5 > ln (1) ; 1-x / 5 >0 ; x / 5 <1 ; x <5.

QCM 6 :
La limite de x² −x ln(x) quand x tend vers +∞ vaut :
A. −∞
B. +∞ vrai.
C. 0
D. n’existe pas.
x² (1-ln(x) / x ).
Au voisinage de l'infini : ln(x) / x tend vers zéro ; 1-ln(x) / x tend vers 1.
Par produit des limites x² (1-ln(x) / x ) tend vers l'infini.

QCM 7 :
Le nombre de solutions de l’équation définie sur R+* : 2(lnx)² +3lnx −5 = 0 est :
A. 0
B. 1
C. 2, vrai.
D. 3
On pose X = ln(x) ; 2X²+3X-5 = 0 ; discriminant D = 3²+4 x2x5 =49 ; D^½ = 7.
X₁ = (-3 +7) / 4 = 1 soit x = e.
X₁ = (-3 -7) / 4 = -2,5 soit x = e^-2,5.

.
.

Exercice 2
QCM 8 :
La fonction h définie sur R par h(x) = ln(4+x²) est dérivable sur R.
Sa dérivée est la fonction h′ définie sur R par h′(x) =
A. 1/(4+x²)
B. −2x/(4+x²)
C. x/(4+x²)
D. 2x/(4+x²). Vrai.
On pose u =4+x² ; u' = 2x ; h'(x) = u' / u = 2x/(4+x²).

QCM 9 : Une primitive de la fonction f définie sur ]0 ; +∞[ par f (x) =2 /x +e^3x est :
A. F(x)= 2ln(3x)+1/3 e^3x. Vrai.
On dérive F(x) : 2 x3 /(3x)+3 / 3e^3x= f(x).
B. F(x)= −2 /x² +3e^3x. C'est la dérivée de f(x)
C. F(x) = 2ln(3x)+3e^3x. 3e^3xest la dérivée de e^3x.
D. F(x)= 2ln(x)+3e^2x. L'exposant de l'exponentielle diffère de trois.

QCM 10 :
La forme exponentielle du nombre complexe −2i /(3+3i) est :

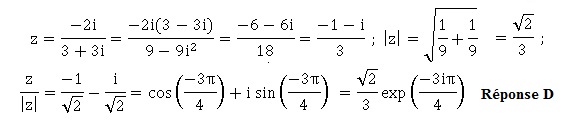
QCM 11 :
Une maladie survient chez 1% des individus d’une population. Quand le sujet est porteur d’un certain génotype G, il a 20 chances sur 100 de développer la maladie. Quand il ne le porte pas, il a cent fois moins de chance de développer la maladie. Quelle est la fréquence à 10⁻² près du génotype G ?
A. 0,01
B. 0,02
C. 0,03
D. 0,04, vrai.

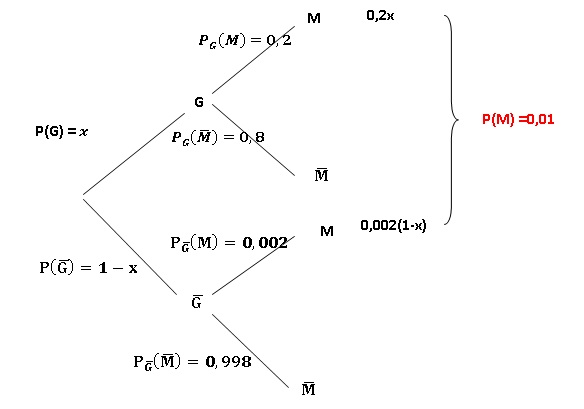
0,2x +0,002(1-x) = 0,01 ; 0,198x =0,008 ; x ~0,04.

QCM 12 :
P est une loi de probabilité sur [1 ; 10] de densité f définie sur [1 ; 10] par f (x) = l x⁻².
Le réel l vaut :
A. 10 / 9
B. 2 / 3
C. 1
D. 4 / 3.

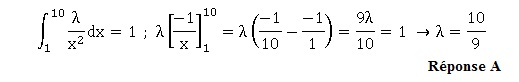
QCM 13 :
Dans une maternité, on a constaté que 10% des accouchements avaient lieu avant terme et que 20% des accouchements présentaient des complications. De plus, les accouchements ayant lieu avant terme ou présentant des complications représentent 26% des accouchements.
Les évènements « accouchement avant terme » et « accouchement avec complication » sont :
A. compatibles et dépendants, vrai.
B. compatibles et indépendants
C. incompatibles et dépendants
D. incompatibles et indépendants
On définit les événements : A " accouchement avant terme" ; B " avec complications".
P(A) =0,10 ; P(B) = 0,20 ; P(A u B) =0,26.
P(A u B) = P(A) +P(B) -P(A n B) ; P(A n B) =0,10 +0,2 -0,26 = 0,04 différent de P(A) +P(B).
Les deux événements ne sont pas indépendants.
P(A n B) différe de zéro : les événements sont compatibles.

QCM 14 :
La maladie humaine appelée phénylcétonurie se transmet comme un caractère récessif, la phénylcétonurie étant portée par l’allèle p et l’état normal par P. On suppose que 90% des personnes ayant le génotype p/p sont affectées par cette maladie et que les personnes qui sont soit P/P, soit P/p, n’en souffrent pas.
Deux parents, l’un de génotype P/p et l’autre de génotype p/p décident de concevoir un enfant. La probabilité pour un enfant de ce couple d’être atteint de phénylcétonurie est :
A. 0,9
B. 0,45, vrai.
C. 0,23
D. 0,11
l'un des parents fournit l'allèle p et l'autre l'allèle p ou P. Donc deux possibilités équiprobables : p /p ou p /P.
0,90 / 2 = 0,45.

Exercice 3.
Lorsque l’on prend un médicament, il est peu à peu éliminé par l’organisme. La concentration d’un médicament présent dans le sang après t heures est : C(t ) =C₀e^−kt
avec :
• t le temps exprimé en minutes ;
• C(t ) la concentration à l’instant t exprimée en mg.L⁻¹ ;
• C₀ la concentration à l’instant 0 ;
• k un coefficient qui dépend du patient et du médicament.
On rappelle que pour tout x ∈ R, exp(x) = e^x .
1. a. On appelle demi-vie la durée T au bout de laquelle la concentration a diminué de moitié. Calculer T.
0,5C₀ =C₀e^−kT ; 0,5 =e^−kT ; ln(0,5) = -ln(2)= -kT ; T = ln(2) / k.
b. Au bout de 4 demi-vies, le médicament est-il éliminé à plus de 10%? Justifier.
A chaque demi-vie , la concentration est divisée par 2. Au bout de 4 T, la concentration vaut C₀ / 2⁴ ~ 0,0625 C₀.
2. Dans cette question, on considère un patient donné qui absorbe par voie orale un médicament donné. Le principe actif n’est pas immédiatement présent dans le sang.
Sa concentration est modélisée par la fonction D définie sur [0 ; +∞[ par :
D(t ) = 8·[exp(-t /100)−exp(−et / 100)] ¶¸
a. Étudier la limite de la fonction D lorsque t tend vers +∞.
Au voisinage de l'infini, les deux termes en exponentielle tendent vers zéro. D(t) tend vers zéro.
b. Montrer que la dérivée D′ de la fonction D sur l’intervalle [0 ; +∞[ est donnée par :
D′(t ) = −2 / 25 exp(−et / 100) [exp(t(e-1) /100 -e].
D'(t) = 8 [-0,01 exp(-t /100) + 0,01e exp(−et / 100)].
D'(t) = -0,08 [ exp(-t /100) - e exp(−et / 100)].
D'(t) = -2 /25 [ exp((e-e-1)t /100) - e exp(−et / 100)].
D'(t) = -2 / 25 exp(-et /100) [ -e+ exp((e-1)t / 100) ].
c. Étudier les variations de la fonction D.
exp(-et /100) >0 ; -2 / 25 exp(-et /100) <0 ;
D'(t) = 0 si : -e+ exp((e-1)t / 100) = 0 ; exp((e-1)t / 100) = e¹ ; (e-1)t / 100) = 1 ; t = 100 / (e-1).
-e+ exp((e-1)t / 100) >0 si t >100 / (e-1).
D'(t) >0 si t <100 / (e-1). D(t) est strictement croissante.
D'(t) <0 si t >100 / (e-1). D(t) est strictement décroissante.
D'(t) est nulle pour t = 100 / (e-1). D(t) présente un maximum.
d. Déterminer la concentration maximale D_max.
D_max = 8·[exp(-1 / (e-1))−exp(−e / (e-1))] =8 (0,5588 -0,2056) ~2,82.

.

menu