Mathématiques, probabilités, concours Avenir 2016

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


Probabilités conditionnelles.
47. On considère deux événements A et B non indépendants tels que P(A)=0,3 , P(B) = 0,6.

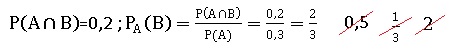
Réponse a.

 48. On considère deux événements A et B tels que P(A) = 0,8 ; P(B) = 0,5 et PA(B) = 0,4.

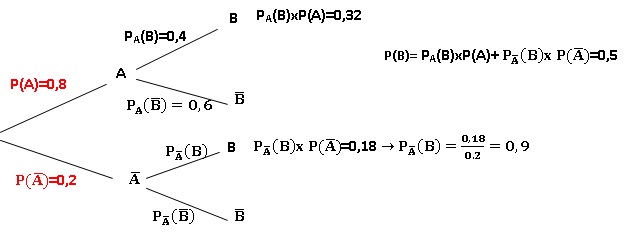Réponse d.

49. On lance 2 dés cubiques non truqués dont les faces sont numérotées de 1 à 6. Quelle est la probabilité d'obtenir une somme strictement supérieure à 5 sachant que les 2 numéros obtenus sont différents ?
11 cas favorables : 1+5 ; 1+6 ; 2+4 ; 2+5 ; 2+6 ;  3+4 ; 3+5 ; 3+6 ; 4+5 ; 4+6 ; 5+6.
15 cas possibles : 1,2 ; 1,3 ; 1,4 ; 1,5 ; 1,6 ; 2,3 ; 2,4 ; 2,5 ; 2,6 ; 3,4 ; 3,5 ; 3,6 ; 4, 5 ; 4, 6 ; 5,6.
La probabilité de cet événement est donc 11 /15. Réponse b.
Lois de probabilités.
 50. Soit X une variable aléatoire continue qui suit une loi uniforme sur[ 0 ; 12 ] alors P(X>4)(X<6)=
 a. 0,25 Vrai ; b. 0,5 ; c.1/3 ; d. aucune des réponses précédentes.
Chaque événement a la même probabilité soit 1 / (12-0)=1/12..
Probabilité que X soit supérieur à 4 : P(X>4) = 8 / 12.
probabilité que X soit inférieur à 6 et supérieur à 4 : 2/12.
Probabilité que X soit inférieur à 6 sachant que X est supérieur à 4 : 2/8=0,25.

51. Un coursier fait une livraison quotidienne, son passage à mon bureau est réparti aléatoirement de façon uniforme entre 10 h et 12 h 30 min. Sur un grand nombre de jours, à quelle heure puis-je, en moyenne, espérer le voir passer ?
a : 10h45 ; b : 11h ; c : 11h15 Vrai ; d : 11h30.
(10 +12,5) / 2=11,25 h ou 11h15 min.
.
.





52. Soit X une variable aléatoire continue qui suit une loi exponentielle de paramètre l telle que E(X)=6. Soit h appartenant à [0 ; +oo[ tel que P(X >h)=0,3, alors P(X>6)(X>6+h)=
a : 0,18 ; b : 0,3 Vrai ; c : 0,5 ; d : 0.
P(X>6) = exp(-6l) ; P(X>6+h) = exp(-(h+6)l) ;
P(X>6)(X>6+h)= exp(-(h+6)l) /  exp(-6l)  =exp(-hl) =P(X> h) = 0,3.

53. Soit une variable aléatoire continue qui suit une loi normale centrée réduite, on note µ l'espérance mathématique de X  et s l'écart-type de X , alors :
a : µ=0 et s = 1, Vrai ; b : µ=1 et s = 1 ; c : µ= -1 et s = 1 ; d : µ=1 et s = 0.

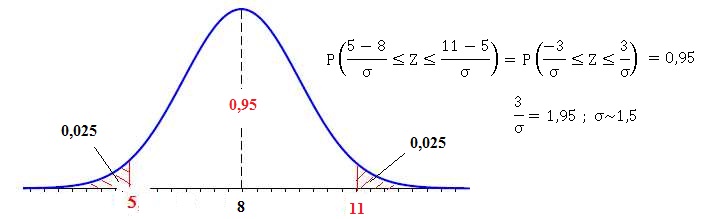
54. Soit X une variable aléatoire continue qui suit une loi normale d'espérance mathématique 8 et d'écart-type s. On sait que P(5 < X <11)=0,95, alors :
a : s=1 ; b : s=0,5 ; c s=3 ;  d : s=1,5 Vrai.









55.  Soit X une variable aléatoire continue qui suit une loi normale d'espérance mathématique 4 et d'écart-type 2. Alors
P(X>2)(2<X<6) ~
a. 0,5. b. 17 /21 Vrai;  c. 95 /97,5 ; d.99 / 99,5.

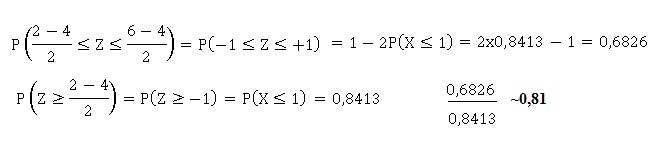
Algorithme.
On considère l'algorithme suivant :
Variables :
I, N , U : nombres
Traitement :
Saisir un entier N
Affecter à U la valeur 2
Pour I allant de 1 à N par pas de 1 faire
Si U est pair alors affecter à U la valeur U /2
sinon affecter à U la valeur 3U+1
Fin du si
Fin du pour
Afficher U

56. Si on fait fonctionner l'algorithme avec N=4, on obtient comme affichage :
a. 1 Vrai ; b. 3,5 ; c. 4 ; d. aucune des réponses précédentes.
N
 1
 2
 3
 4
 5
 6
 7
 8
 9
 10
 11
U
 1
 4
 2
 1
 4
 2
 1
 4
 2
 1
 4

57. Si on fait fonctionner l'algorithme avec N=55, on obtient comme affichage :
a. 2  ; b. 1 Vrai ; c. 25 ; d. aucune des réponses précédentes.

58. Par quelle condition doit-on remplacer "Si est pair" si on désire programmer cet algorithme. Dans les quatre réponses suivantes E(X) désigne la partie entière du nombre X .
a. Si U-E(U)=0 ; b. Si 2U-E(2U)=0 ; c.Si U-2E(U/2)=0. Vrai ; d. Si U/2- 2E((U+1)/2)=0

Statistiques.
59. On  considère la série statistique suivante :
Modalités (xi)
 2
 3
 4
 6
 8
Effectifs ( ni)
 8
 18
 16
 12
 5
On désigne par " Mo" le mode de la série et par " Med" la médiane de la série, alors :
a. Mo=3 et Med=3 ; b. Mo=4 et Med=4 ;
c. Mo=5 et Med=4 ; d. Mo=3 et Med=4. Vrai.
La valeur la plus représentée est 3.
Effectif total / 2 = 29,5 ; la médiane vaut 4.



60. On observe un caractère sur un échantillon de taille n, la fréquence f observée permet d'obtenir un intervalle de confiance au seuil de 95 % d'amplitude :


  

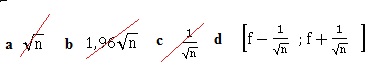
menu