Mathématiques,
équations, fonctions exponentielle et logarithme,
concours Avenir 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Interprétation graphique.
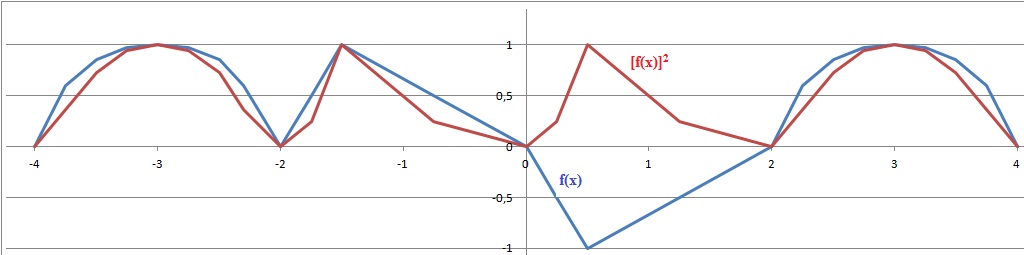
1. La
fonction f (x), courbe bleue :
a. est paire non
impaire.
b.
est impaire, non paire.
c. est paire et
impaire
d.
n'est ni paire, ni impaire. Vrai.
Une fonction paire est symétrique par rapport à l"axe des y ; une
fonction impaire est symétrique par rapport à l'origine.
2. L'équation f(x)=0 admet :
a. 2 solutions ; b. trois
solutions ;
c. quatre solutions ;
d. cinq solutions. Vrai.
( -4 ; -2 ; 0 ; 2 ; 4 )
3. L'équation f
'(x)=0 admet :
a : deux solutions.
Vrai. ( -3 et +3 ).
b : trois solutions
. c : quatre solutions. d : cinq solutions.
4.
L'équation f(x) x f '(x)=0 admet :
a : 2 ou 3
solutions. b : 4 ou 5
solutions. c : 6 ou 7
solutions. Vrai. d : 8 ou 9 solutions.
5.
L'équation [f(x)]2=1 admet : ( voir courbe rouge )
a : 2 solutions. b : 3 solutions. c : 4 solutions. Vrai. ( -3 ; -1,5 ; 0,5 ; 3 )
d : aucune des
trois propositions ci-dessus n'est correcte.
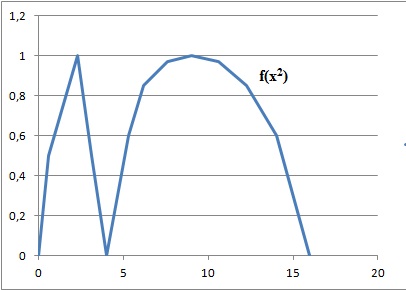
6. L'équation f(x2)=1
admet :
a : 2 solutions
Vrai ( 0,5 ; 3 ). b : 3 solutions. Vrai ( -3 ; -1,5 ; 3 ). c : 4 solutions.
d : aucune des trois propositions
ci-dessus n'est correcte.
7. L'aire A
appartient à :
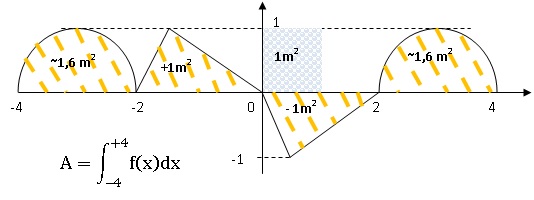
a : [2 : 3 ]. b : [3 ; 4 ] Vrai. c : [4 ; 5 ]. d : [5 ; 6 ].
A est égale à l'aire du disque de rayon R = 1 m soit p m2.
8. B est égale à :
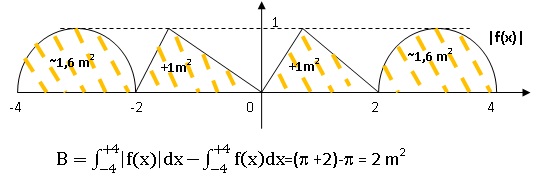
a : un entier
naturel. Vrai.
b : un décimal non
entier.
c : Un rationnel
non décimal.
d : un irrationnel.
|
| .
. |
|
|
Fonctions exponentielle et logarithme.
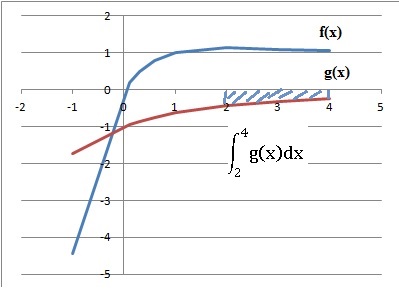
Soient les fonctions f et g respectivement définies sur R et R+ par f(x) = e-x(x-1)+1 ; g(x) = (e-x-1) / x.
13. Quand x tend vers l'infini, la limlite de f(x) est égale à :
a : -oo. b : +oo. c : 0.
d : aucune des réponse précédentes. Vrai..
Quand x tend vers plus l'infini : par croissance comparée (x-1)/ex tend vers zéro et f(x) tend vers 1.
14.Quand x tend vers moins l'infini, la limlite de f(x) est égale à :
a : -oo Vrai.. b : +oo. c : 0.
d : aucune des réponse précédentes.
Quand x tend vers moins l'infini : e-x tend vers +oo et (x-1) tend vers -oo ; f(x) tend vers -oo.
15. Quand x tend vers plus l'infini, la limlite de g(x) est égale à :
a. -oo. b. +oo. c : 0 Vrai.
d : aucune des réponse précédentes.
Quand x tend vers plus l'infini : e-x tend vers zéro ; e-x / x tend vers zéro ; 1/x tend vers zéro.
16. Quand x tend vers zéro, la limlite de g(x) est égale à :
a. 0. b. 1. c : -oo ou +oo.
d : aucune des réponse précédentes. Vrai.
Au voisinage de zéro, e-x est équivalent à 1 -x +0,5 x2 ; e-x-1 est équivalent à -x +0,5 x2 ; g(x) est équivalent à -1+0,5 x ~-1.
17. Sur R∗, la fonction g ′ est définie par g'(x) :
a. [e-x(x-1)+1] / x2.
b. [e-x(x+1)+1] / x2.
c. [e-x(-x-1)+1] / x2.Vrai.
d. [e-x(-x+1)+1] / x2.
On pose u = e-x-1 et v = x ; u' = -e-x ; v' = 1.
(u'v -v'u ) / v2=[ -xex-(e-x-1)] / x2 = [e-x(-x-1)+1] / x2.
18. La primitive F de f sur R telle que F(0) = 0 est définie par F(x) =
a. -e-x(0,5x2-x)+x ; b. e-x(0,5x2-x)+x ; c. x(1-e-x) Vrai.; d. aucune des réponses précédentes.
Dériver les expressions proposées :
a. e-x(0,5x2-x)-e-x(x-1)+1 diffère de f(x).
b. -e-x(0,5x2-x)+e-x(x-1)+1 diffère de f(x).
c. (1-e-x)+xe-x=f(x).
19. La primitive de g(x) sur l'intervalle [2 ; 4] est
a. nulle; b. strictement négative. Vrai ; c. strictement positive ; c. aucune des propositions précédentes.
(voir aire hachurée ci-dessus)
.
20 . Sur R+, f est : a. constante ; b. strictement décroissante ; c. strictement croissante ; d. non monotone. Vrai.
.
21. L'équation ln[f(x) ] = 0 a même(s) solution(s) que l'équation :
a. racine carrée (x)=1 Vrai ; b. x2=1 ; c. ex=1 ; d. aucune des trois propositins précédentes
ln[f(x) ] = ln[e-x(x-1)+1] =ln 1 soit e-x(x-1)=0 ; solution x =1.
x2=1 admùet deux solutions x = ±1.
22.f [ln(1)] appartient à :
a. ]-oo ; 0[ ; b. [0 ; 2[ Vrai ; c. [2 ; 4[ ; d.[ 4 ; +oo[
f [ln(1)]= (ln(1)-1) / eln(1)+1=(0-1) / 1 +1 =0.
|
|
|
|
Fonctions.
Soient f la fonction définie et dérivable sur R telle que f ′(x) =1/(1+x4) et f (0) = 0 et g la fonction définie sur R par g (x) = f (−x).
23. Sur R, f est :
a. constante ; b. strictement décroissante.c. strictement croissante. Vrai.
d. Aucune des 3
réponses précédentes n'est exacte.
f '(x) est positive sur R ; donc f(x) est strictement croissante sur R.
24. g'(x) = :
a. -f '(-x) ; b. f '(-x) Vrai ; c.f '(x) ; d. Aucune des 3 réponses précédentes
n'est exacte.
On pose u = -x ; u'= -1 ; g'(x) = -g'(-x)= -f '(-x).
25. Le plus grand ensemble sur lequel g(x) est positif ou nul est
a. R ; b. R- Vrai ; c. R+ ; d. R*.
26. Sur R, g(x) est :
a.constante ;
b. strictement décroissante Vrai
; c. strictement ctoissante ; d. non monotone.
g '(x) est négaitive sur R ; donc g(x) est strictement décroissante sur R.
27. La primitive de f(x) sur [-1 ; 1] est :
a. nulle
Vrai ; b. strictement négative
; c. strictement positive
; d. Aucune des trois propositions proposées n'est correcte.
f(x) est strictement croissante et f(0)=0.
Equations et inéquations.
28. Sur [-p ; p] le nombre de solutions de l’équation cos(2x)+1 = 0 est égal à :
a.1 ; b. 2
Vrai ; c. 3
; d. 4.
cos(2x) = -1 = cos (p) ; 2x = ±p +2kp ; x = ±p/2+kp.
29. Sur [-p ; p] l'inéquation 2cos (x) +3½<0 a pour solution :
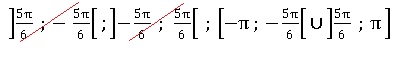 réponse c. réponse c.
cos (x) < -3½/2 ; cos (x) < cos (5p/6)
30. Sur R, le nombre de solutions de l’équation e1/x = 1/ex est égal à
a. 0 Vrai;
b. 1; c. 2 ; d. aucune des propositions précédentes.
e1/x *ex =1 ; exp(1/x+x)= 1 ; 1/x+x = ln (1) = 0 ; 1/x =-x ; x2=-1, impossible.
31. Sur R, une équation équivalente à l’équation ln(3x +10) = 2ln(−x) est :
a. ln((3x +10)/(-x)=2 ;
b. ln(3x +10) = ln(x)2=
; c. ln((-x)2 -3x-10)=0 ; d. aucune des propositions précédentes.. Vrai
ln(3x +10) - 2ln(−x)=0 ; ln(3x +10) - ln(−x)2=0 ; ln((3x +10)/x2)=0.
|
|