Mathématiques,
concours Avenir 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Simplifications d'écritures.
1. 0,5
ln(27)-2ln(3)+ln(3½) est :
a. nul. Vrai.
b.
strictement positif.
c. strictement
négatif
d.
aucune des trois propositions ci-dessus n'est correcte.
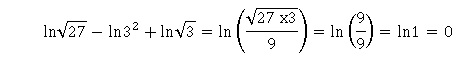
Une fonction paire est symétrique par rapport à l"axe des y ; une
fonction impaire est symétrique par rapport à l'origine.
2. L'expression suivante est égale a
:
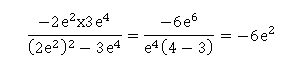 Réponse b Réponse b
3. (ln(3))2
-2 ln(3) est :
a : nul. . b : strictement négatif. Vrai. c : strictement positif. d : aucune
des trois propositions ci-dessus n'est correcte.
ln(3) (ln(3)-2) ; ln(3) est positif ; ln(3)-2 est négatif.
4.
L'expression suivante est égale à :
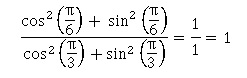 Réponse b. Réponse b.
Continuité et dérivabilité. Soit f
une fonction définie sur R.
5.
f est continue en -1 signifie que :
a : la limite de
f(x), quand x tend vers -1, est un réel.
b : la limite de f( x-1),
quand x tend vers zéro, est un réel.
c : la limite de
[f(-1+x) -f(-1) ] / x, quand x tend vers zéro, est un réel.
d : aucune des
trois propositions ci-dessus n'est correcte. Vrai.
La fonction f est continue en -1 signifie que la limite de f(x), quand
x tend vers -1, est égale à (-1).
6. f est dérivable en -1 signifie
: :
a : la
limite de f(x), quand x tend vers -1, est un réel.
b :
la limite de f(
x-1), quand x tend vers zéro, est un réel.
c : la
limite de [f(-1+x) -f(-1) ] / x, quand x tend vers zéro, est
un réel. Vrai.
d :
aucune des
trois propositions ci-dessus n'est correcte.
f est dérivable en -1 signifie que la limite du taux d'accroissement en
-1 est un réel.
Soit g une fonction définie sur [-1 ; 2 ] telle que g(-1)=2 ; g(0) = 1
; g(1) = 0 et g(2)=-1.
7. On
est certain que sur [1 ; 2 ] :
a : g est
strictement décroissante. b :
g est strictement croissante.
c :g n'est pas
strictement décroissante. d :
g n'est pas strictement croissante. Vrai.
On ignore ce qui se passe entre les valeurs proposées. On peut juste
dire que g n'est pas strictement croissante.
8. On est certain
que sur [1 ; 2 ], l'équation g(x) = 0,5 : :
a : n'admet pas de
solution.
b : admet une
uniqque solution..
c : admet au moins
une solution.
d : aucune des trois
propositions ci-dessus n'est correcte.
Vrai.
On ignore si la fonction est continue. Le théorème des valeurs
intermédiaires ne s'applique pas et on ne peut pas connaître le
nombre de solutions.
|
| .
. |
|
|
Equations et inéquations.
9. 1 /x
inférieur ou égal à 0,2 a pour soluion :
a :
]0 ; 5]. b : [5 ; +oo[ . c
: ]-oo ; 5]. d : aucune
des réponse précédentes.
Vrai.
Si x est positif : x est supérieur ou égal à 5.
Si x est négatif, 1/x est toujours négatif, donc inférieur à 0,2.
Solutions : ]-oo ; 0[ union [5 ; +oo[.
10. Le nombre de solutions de l'équation :ln(x2
)= -(ln(x))2 est :
a :
0.. b :
1. c :2. Vrai. d : aucune des réponse précédentes.
2
ln (x) +ln(x) ln(x) = 0 ;ln(x) (2 +ln(x)) = 0.
Solution x = 1 et x = e-2.
11. Le nombre de
solutions de l'équation :(ln(x))2 = -(ln(x))2 est
:
a :
0.. b :
1 Vrai. c :2. d : aucune des réponse précédentes.
ln(x)
ln (x) +ln(x) ln(x) = 0 ; 2ln(x)ln(x) = 0.
Solution x = 1.
12. Le nombre de solutions de l'inéquation
exp(-x2) supérieur ou égal à 1 est :
a.
infini. b. 0. c : 1. Vrai. d : aucune des réponse précédentes.
-x2 supérieur ou égal à 0 ; x2 inférieur ou égal
à 0 ; x =0.
13.
Le nombre de complexes distincts solutions de l'équattion : 2z2
-5z+3=0 est égal à :
a. 0. b. 1.
c. 2. Vrai.
d. aucune des
solutions précédentes.
Discriminant D = (-5)2 -4 x3x2=25-24 = 1.
Solutions ; z1 = (5-1) / 2 = 2 ; z2 =(5+1) / 2 =
3.
Les réels font partie des complexes, il y a deux solutions complexes.
Implications et
équivalences.
Dans les quatre items suivants, P1 et P2 sont
deux propositions et a et b deux réels. De manière générale :
14.
Si P1 : "a3 = b3" et P2
:"a=b" alors :
a. seule P1
implique P2 ; b. seule P2 implique P1 ; c. P1 et P2
sont équivalentes Vrai ; d.
aucune des réponses précédentes.
La fonction f(x) = x3 est strictement croissante.
15. Si P1
:"ln(a) = ln(b)" et P2 : "ea = eb"
alors :
a. seule P1 implique P2 Vrai ; b.
seule P2 implique P1. c.
P1 et P2 sont
équivalentes ; d. aucune des propositions
précédentes.
ln(a) = ln(b) implique ea
= eb .
ea = eb implique ln(a) = ln(b) seulement si a et b sont
positifs.
16 . Si
P1 :"a2 = b" et P2 :"a = b½"
alors :
a. seule P1 implique P2 ; b. seule P2 implique P1 Vrai
.
c. P1
et P2 sont équivalentes ; d.
aucune des propositions précédentes.
a2 = b
donne a = ±b½.
a = b½ donne b = a2.
17.
Si P1:"AB2=AC2+BC2" et P2
:"ABC est un triangle rectangle", alors :
a. seule P1 implique P2 Vrai ;
b. seule P2 implique P1 . c. P1
et P2 sont équivalentes ; d.
aucune des propositions précédentes.
Il n'est pas précisé quel est l'angle droit dans le triangle rectangle
ABC.
|
|
|
|
Interprétation
graphique.
Ci-dessous la parabole représentant la fonction f définie sur R.
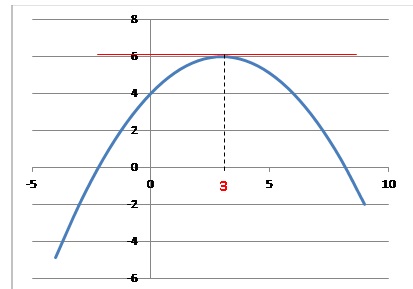
Soient les suites (Un) et (Vn) définies, pour
tout entier naturel n respectivement par : Un = f(n) et V0
= a ; Vn+1 = f(Vn) où a est un réel.
18. La
tangente à la parabole au point d'abscisse 3 a pour équation :
a. x=6 ; b. y=6. Vrai.
c. y = 6x-18.
d. Aucune des 3
réponses précédentes n'est exacte.
La tangente est horizontale ( y = 6) au point d'abscisse x = 3.
19. La dérivée est
définie par f '(x) = :
a. -4x /9 -4/3 ; b. -4x/9 +4/3 Vrai ; c. 4x/9 -4/3 ; d. 4x/9+4/3.
La dérivée doit s'annuler pour x = 3, être négative pour x >3 et
positive pour x <3.
20. Quand x tend
vers l'infini, la limite de f(x)-x est égale à :
a. -oo . Vrai; b. +oo ; c.
0 ; d. aucune des
proposition proposée.
Equation de la parabole y = -2x2 /9 +4x/3 +4.
Au voisinage de l'infini, f(x) -x est équivalent à -2x2/9.
21.
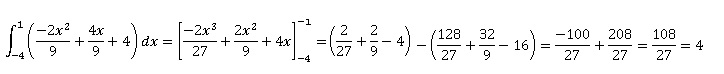 Réponse c. Réponse c.
22. La suite (Un)
est :
a. minorée non
majorée ; b. majorée non
minorée vrai ; c. bornée ;
d. Aucune des trois
propositions proposées n'est correcte.
La suite est majorée par u3 = 6.
23. Pour a = 1, V2
appartient à :
a.[0 ; 2] ; b. [2 ; 4] ; c.
[4 ; 6 ] vrai
; d. Aucune des trois
propositions proposées n'est correcte.
V0 = 1 ; V1 = f(1) ~5,11 ; V2 =
f(5,11) ~5,0.
24. Pour a = -1, la
suite (Vn) est :
a. constante ;
b. strictement
décroissante ; c. strictement
croissante ;
d. Aucune des trois
propositions proposées n'est correcte. Vrai.
V0 = -1 ; V1 = f(-1) ~2,4; V2 = f(2,4)
~5,9 ; V3 = f(5,9) ~4,1.
La suite n'est pas monotone.
25. Pour a = -4,
la suite (Vn) est :
a. convergente ; b. diverge vers -oo, vrai ; c. diverge vers +oo ; d. aucune des propositions
précédentes.
V0 = -4 ; V1 = f(-4) ~-5; V2 = f(-5) ~
-8,2 ; V3 = f(-8,2) ~ -22.
Trigonométrie.
Soit f la fonction définie sur R par f(x) = x cos (x/3).
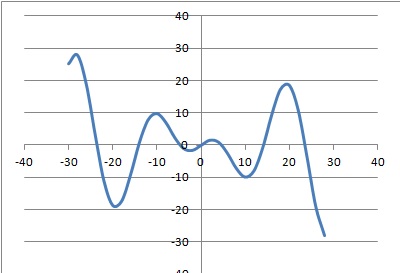
26. f est :
a.paire ; b. impaire
Vrai; c. paire et impaire ; d. aucune des
propositions précédentes.
La fonction cos (x/3) est paire; f(-x) = -x cos (-x/3) = -x cos (x/3) = -f(x)..
27. f est :
a. périodique de période 2p.
b. périodique de période 6p. Vrai.
c. périodique de période 2p/3.
d. aucune des
propositions précédentes. Vrai.
cos (x+6p)/3)= cos (x/3 +2p) = cos (x/3).] de l'équation f(x) = 0 est :
Mais (x+6p) cos(x/3) diffère de x cos (x/3) : f n'est pas périodique.
28. Le nombre de solution sur [-2p ; +2p] de l'équation f(x) = 0 est :
a. 0 ; b. 1 ; c. 2 ; d. 3. Vrai.
x = 0 ; cos (x/3) = 0 = cos (±p/2) ; x/3 = ±p/2 ; x = ±3p/2.
29. Sur R la fonction f '(x) est définie par :
a.-x sin (x/3).
b. cos(x/3) +x sin (x/3).
c. cos (x/3)-x sin (x/3).
d. aucune des
propositions précédentes. Vrai.
On pose u = x et v = cos(x/3) ; u'=1 ; v' = -1/3 sin (x/3).
u'v+v'u = cos(x/3) -x/3 sin (x/3).
30. Sur R la primitive F de f telle que F(0)=0 est définie par :
a. x2/2 sin (x/3).
b. 3x2/2 sin (x/3).
c. 9 cox (x/3) +3x sin (x/3).
d. aucune des
propositions précédentes. Vrai.
Dériver chaque proposition :
(a) : x sin (x/3) + x2/6 cos (x/3).
(b) : 3x sin(x/3) +x2/2 cos (x/3).
(c) : -3sin (x/3) +3 sin(x/3) +x cos (x/3)= x cos (x/3).
F(0) = 9 cos (0) +3 x0 sin (0) = 9. La condition F(0) =0 n'est pas vérifiée.
31. Quand x tend vers l'infini, la limite de f(x) est égale à :
a. 0.
b. -oo.
c. +oo.
d. aucune des
propositions précédentes. Vrai.
La fonction n'a pas de limite : elle s'annule de manière périodique,
admet des maximum de plus en plus grands et des minimum de plus en plus
négatifs.
32. Quand x tend vers l'infini f(1/x) est égale à :
a. 0. Vrai.
b. -oo.
c. +oo.
d. aucune des
propositions précédentes.
La limite de f(1/x) quand x tend vers l'infini est égale à la limite de f(x) quand x tend vers zéro.
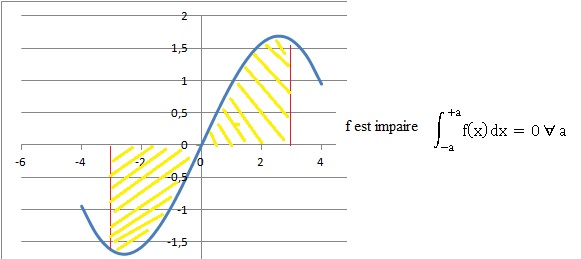
33. Sur R la primitive de f(x) entre -p et +p est :
a. nulle. Vrai.
b. strictement négative.
c. strictement positive.
d. aucune des
propositions précédentes.
|
|