QCM mathématiques.
Concours Advance 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
1. Limites.
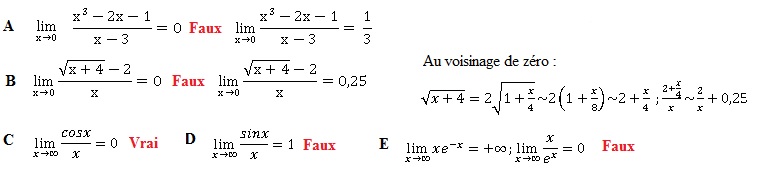
2. Fonction numérique.
a, b, c réels.
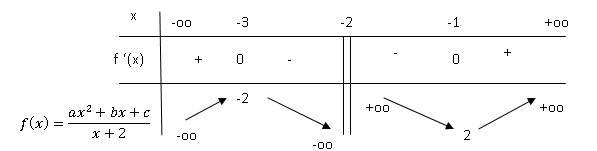
A.
f(-2)= -3. Faux, f(x) n'est
pas définie pour x = -2.
B. a >0. Vrai. Quand x tend vers -oo, f(x)
est équivalente à ax.
x étant négatif, la limite étant négative, alors a est positif.
C. f(0) >0. Vrai. f(x) est croissante sur [-1 ;
+oo[[ et f(x) est minorée par 2 sur cet intervalle.intervalle.
D. c>0. Vrai. f(0) = ½c positif.
E. b2-4ac
>0. Faux. Le numérateur ax2+bx+c
n'est jamais nul. ax2+bx+c=0 n'a pas de solution
dans R.
3. Fonction exponentielle.
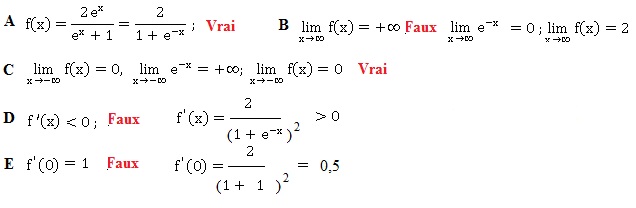
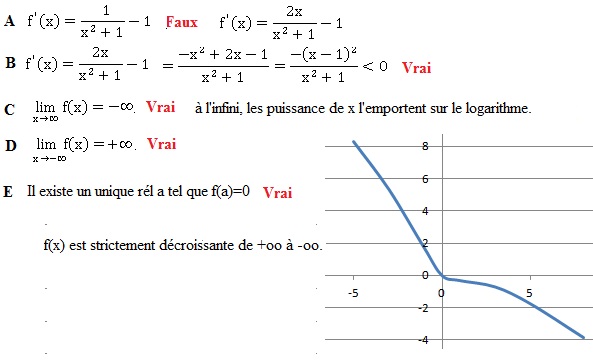
4. Fonction logarithme.
f(x) = ln(x2+1)-x.
Dérivée : on pose u = 1+x2 ; u' = 2x. f '(x) = u' / u -1.
|
| .
. |
|
|
5. .
Pour tous réels non nuls a, b, c et d on a :
A. Si a < b
alors a2 < b2.
Faux si a et b sont inférieurs à 1.
B. Si a2
< b2 alors a < b. Faux.
C. Si a < b et c
< d alors ac < bd. Faux.
D. Si a < 0 < b alors 1/b <
1 /a. Faux.
E. Si ac < bd alors c / b < d
/a. Faux.
6.
A. "Il existe x réel , il existe y réel x < y " est une proposition
vraie. Vrai.
B. "Pour tout x réel , pour tout y réel x < y " est une proposition
vraie. Faux.
C. "Pour tout x réel, il existe y réel x < y " est une proposition
vraie. Vrai.
D. "Il existe x réel , pour tout y réel x < y " est une proposition
vraie. Faux.
E. "Pour tout x réel , il existe y réel x < y " est équivalent à
"Il existe x réel , pour tout y réel x < y ". Faux.
7.
Soit f une fonction continue sur R vérifiant f (0) = 0 et f (1) = 4 .
On pose g la fonction définie par g(x) = f(x+0,5)-f(x)-2. . Alors :
A. g est continue sur R. Vrai.
B. g (0) < 0. Faux.
g(0) = f(0,5) -f(0)-2 =f(0,5)-2 , le signe de g(0)dépend de la valeur de f(0,5).
C. g(0) g(0,5) est négatif ou nul. Vrai.
g(0,5) = f(1) -f(0,5) -2 = 4-f(0,5)-2 = 2-f(0,5).
g(0) g(0,5) = [f(0,5)-2 )] [2-f(0,5)] =-[f(0,5)-2]2.
D. Il existe c réel tel que f(c+0,5)-f(c) =2. Vrai.
f(c+0,5)-f(c) = g(c) +2 ; g(c) +2 =2 ; g(c)=0.
E. Pour tout x réel, f (x) = 4x. Faux..
8. Soit f la fonction définie sur R par : f (x) = 4cos2 (x) -3 .Alors :
A. Il suffit d'étudier f sur 0,p. Vrai.
f(x) = 4(cos(2x)+1) / 2 -3 = 2 cos(2x) -1.
cos(2x) est périodique de période p.
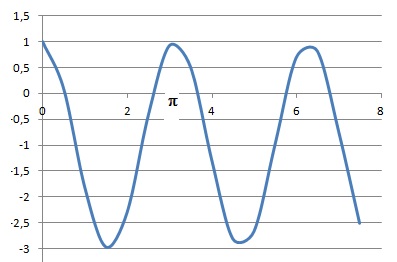
B. Pour tout x réel, f (x -p ) = f (x). Vrai.
cos(2x-2p = cos(2x).
C. f est dérivable sur R et pour tout x de R, f '(x) = -4sin (2x). Vrai.
On pose u = 2x ; u' = 2 ; dérivée de cos(2x) = -2sin(2x) ; f '(x) = -4 sin(2x).
D. f est décroissante sur 0 ; 0,5 p. Vrai.
E. f est décroissante sur - 0,5 p ; 0. Faux.
|
|
|
|
9. Pour toute suite réelle (un) on a :
A. Si pour n tendant vers l'infini, la limite de un vaut 1, alors un=1 à partir d'un certain rang. Faux.
B. Si pour n tendant vers l'infini, la limite de un vaut 0,5, alors un est positif ou nul à partir d'un certain rang. Vrai.
C. Si pour tout entier n positif un >0 et un converge alors la limite de un est positive quand n tend vers l'infini. Faux.
La limite peut être nulle.
D. Si un est une suite arithmétique de raison -1/3 alors la limite de la suite à l'infini est nulle. Faux.
un+1 =un-1/3.
E. Si un est une suite géométrique de raison -1/3 alors la limite de la suite à l'infini est nulle. Vrai.
un = u0(-1/3)n. La raison de la suite géométrique appartient à ]-1 ; 1 [
10.

11. Un facteur doit distribuer 3 lettres adressées à 3 destinataires distincts. Etant totalement
ivre, il dépose une lettre au hasard dans chaque boîte. Alors la probabilité :
A. que chaque lettre arrive à son destinataire est 1/3. Faux.
Les
lettres sont notées A, B, C. Le facteur distribue les lettres au
hasard, ce qui correspond à choisir une des repartitions suivantes :
ABC ; X=3 et P(X=3)=1/6
ACB ; X=1; BAC ; X=1 ; CBA ; X=1 ;P(X=1)=3/6 =1/2
CAB ; X=0 ; BCA ; X=0 ; P(X=0)=2/6=1/3..
Une seule de ces 6 est la bonne répartition donc la probabilite de A. est 1/6.
B. qu'exactement une lettre arrive au bon destinataire est 1/3. Faux.
p(X=1)=3 / 6 =0,5
C. qu'au moins une lettre arrive au bon destinataire est 0,5. Faux.
P(X>0)=1-P(aucune lettre n'est dans la bonne boite)= 1-1/3=2/3.
D. qu'aucune lettre n'arrive au bon destinataire est 1/3. Vrai.
p(X=0)=2/6
E. qu'exactement 2 lettres arrivent à leur destinataire est 0. Vrai.
Si deux lettres sont bien distribuées, la troisième l'est aussi. Donc X=2 est impossible et donc P(E) = P(X=2) = 0.
12.
Dans une classe, 75 % des étudiants ont préparé l'examen. Un étudiant
n'ayant pas préparé l'examen le réussit avec une probabilité 0.2,
tandis qu'un étudiant l'ayant préparé réussit avec une probabilité 0.9.
Alors la probabilité :
Evénement P : a préparé l'examen ; événement R : a reussi l'examen.
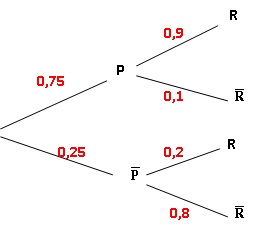
A. qu'un étudiant ne prépare pas l'examen et réussisse est 0.8. Faux.
0,25 x0,2 =0,05
B. qu'un étudiant réussisse l'examen est 0.725. Vrai.
0,75 x0,9 + 0,25 x0,2 =0,725
C. qu'un étudiant n'a pas préparé l'examen sachant qu'il a réussi est 0.25. Faux.
0,25 x0,2 = 0,05.
D. qu'un étudiant échoue à l'examen est 0.275. Vrai.
1-0,725 =
E. qu'un étudiant prépare l'examen et échoue est 0.075. Vrai.
0,75 x0,1 = 0,075.
|
13. Soit (un ) la suite définie par u0 = 0 et pour tout n réel un+1=0,5un+1.
On considère les deux algorithmes suivants:
| Algo1 |
Algo 2
|
Variables n et k entiers naturels, u réel
Initialisation u =0
Entrée saisir k
Traitement Pour n variant de 1 à k
u = 0,5 u+1
Fin Pour
Sortie Afficher u
|
i et r entiers naturels, u réel
Initialisation u=0 ; i = 0
Entrée saisir r
Tant que u < 2-10-r.
u = 0,5 u+1
i = i+1
Fin Tant que
Afficher i.
|
A. L'algo1 calcule le terme uk de la suite ( un). Vrai.
B. Pour k = 3 l'algo1 affiche 1,75. Vrai.
u1 = 1 ; u2 = 0,5 u1+1 = 1,5 ; u3 = 0,5 u2+1 = 1,75.
C. L'algo2 affiche le terme un tel que un soit supérieur ou égal à 2 -10-r. Faux.
D. L'algo2 s'arrête parce que un est majorée par 2. Faux.
E. Après avoir
déroulé l’algo2, si on prend k = i dans l'algo1 alors la valeur
affichée de l'algo1 vérifie supérieur ou égal à 2-10-r. Vrai.
14. On veut construire un algorithme permettant de trouver une valeur approchée à 10-2 près de la solution de l'équation x5 - 4x3 + 2 = 0 appartenant à [0,1].
L'algorithme se présente ainsi :
Variables a , b réels
Initialisation a=0, b=1
Traitement Tant que condition1
Si[ (a+b) / 2]5-4[(a+b) / 2]3+2 >0 alors
affectation1
Sinon
affectation2
Fin Si
Fin Tant que
Sortie Afficher a et b
A. La condition1 est b - a <10-2. Faux.
condition 1 :|b-a| <10-2.
B. L'affectation1 est b = (a+b) / 2. Faux.
affectation 1 : a = (a+b) / 2
affectation 2 : b = (a+b)/2
C. L'affectation1 et l'affectation2 sont les mêmes. Faux.
Itération
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
a
|
0
|
(a+b)/2 =0,5
|
(0,5+1) / 2 =0,75 |
0,75
|
(0,875+0,75) / 2 = 0,8125
|
0,84375
|
0,84375
|
0,84375
|
b
|
1
|
1
|
1
|
(a+b)/2 = 0,875
|
0,875
|
0,875
|
0,859375
|
0,8515625
|
(a+b) / 2
|
0,5
|
0,75
|
0,875
|
0,8125
|
0,84375.
|
0,859375
|
0,8515625
|
0,84765625
|
| [ (a+b) / 2]5-4[(a+b) / 2]3+2 |
1,53
|
0,55
|
-0,17
|
0,208
|
0,025
|
-0,069
|
-0.022
|
0,00136
|
D. L'algorithme affiche le résultat au bout de 6 itérations Faux.
E. Les valeurs affichées peuvent avoir, a priori, leur premier chiffre après la virgule différent. Vrai.
|
|