Calculs num�riques, brevet 2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


 


.
.


(sujet 2013)
Pour r�aliser un abri de jardin en parpaing, un bricoleur a besoin de 300 parpaings de dimensions 50 cm x 20 cm x 10 cm pesant chacun 10 kg.
Il ach�te les parpaings dans un magasin situ� � 10 km de sa maison. Pour les transporter, il loue au magasin un fourgon dont les caract�ristiqus sont :
‐ 3 places assises. ‐ Dimensions du volume transportable  : 2,60 m x 1,56 m x 1,84 m. ‐ Charge pouvant �tre transport�e : 1,7 tonne. ‐ Volume r�servoir : 80 Litres. ‐ Diesel (consommation : 8 Litres aux 100 km).
Tarifs de location du fourgon :
distance maximale ( km / jour) 30 50 100 200 km suppl�mentaire
prix (€) hors carburant 48 55 61 78 2
Un litre de carburant co�te 1,50 €.
Expliquer pourquoi il devra effectuer deux aller-retour pour transporter les 300 parpaings jusqu’� sa maison.
Masse des 300 parpaings : 10*300 = 3 000 kg = 3 tonnes.
Or la charge maximale transporable est 1,7 t : il faut donc effectuer 2 voyages.
Quel sera le co�t total du transport ?
Distance parcourue : 40 km. Le prix de la location est de 55 €.
Consommation : 8*40/100 =3,2 L soit 3,2 *1,5 = 4,8 €. Total 55+4,8 =59,8 €.
Les tarifs de location du fourgon sont-ils proportionnels � la distance maximale autoris�e par jour ?
30 / 48 = 0,625 ; 50/55 =0,91 ; 100 / 61 =1,6.
La distance maximale journali�re autoris�e n'est pas proportionnelle au prix de la location.

Calculer : (15-9 10-3) / 500 = 2,9982 10-2.
Combien faut-il de temps pour parcourir 800 m � la vitesse de 40 km/h ?
40 / 3,6 = 11,11 m/s ; dur�e = 800 / 11,11 =72 s = 1 min 12 s.
Si on triple l'ar�te d'un cube alors par combien est multipli� le volume ?
Le c�t� triple et le volume du cube est �gal � : V =c�t�3 ; le volume est multipli� par 33 soit 27.
Quelle est l'expression factoris�e 25 x2-16 ?
Diff�rence de deux carr�s : (5x-4)(5x+4).
.
.


Calcule PGCD (405 , 315). Pr�cise la m�thode utilis�e et indique les calculs.

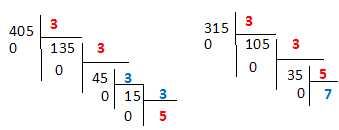
PGCD(405 ; 315) =3*3*5=45.
Dans les bassins d'eau de mer filtr�e d'une ferme aquacole de b�nitiers destin�s � I'aquariophilie, on compte 9 bacs contenant chacun 35 b�nitiers de 12,5 cm et 15 bacs contenant chacun 27 b�nitiers de 17,5 cm.
L'exploitant souhaite r�partir la totalit� des b�nitiers en des lots de m�me composition : par lot, m�me nombre de b�nitiers de 12,5 cm et m�me nombre de b�nitiers de 17,5 cm.
Quel est le plus grand nombre de lots qu'il pourra r�aliser ? Justifie ta r�ponse Quelle sera la composition de chaque lot  ?
Nombre total de petits b�nitiers : 9*35 =315 ; nombre total de grands b�nitiers :15*27 =405.
 405/45 = 9 ; 315 /45 = 7.
Il pourra constituer au plus 45 lots comprenant 7 petits b�nitiers et 7 grands b�nitiers.

.
Dans I'Oc�an pacifique Nord, des d�chets plastiques qui flottent se sont accumul�s pour constituer une poubelle g�ante (qui est, aujourd'hui, grande comme 6 fois la France)
Sachant que la superficie de la France est environ 550 000 km2, quelle est la superficie actuelle de cette poubelle g�ante ?
6*550 000 =3,3 106 km2.
Sachant que la superficie de cette poubelle g�ante augmente chaque ann�e de 10 %, quelle sera sa superficie dans un an ?
3,3 106*1,1 =3,63 106 km2.
Que penses-tu de l'affirmation " dans 4 ans, la superficie de cette poubelle aura doubl� " ? Justifie ta r�ponse.
Dans 4 ans la surface de la poubelle sera multipli�e par : 1,14 =1,46. On est donc loin du double.

Pour chacune des quatre affirmations suivantes, pr�ciser si elle est vraie ou fausse et justifier la r�ponse.
 Le PGCD de 18 et de 36 est 9. Faux.
18 = 2*32 ; 36 = 22*32 ; le PGCD de 18 et 36 vaut : 2*32 = 18.
 Le double de 9 /4 est �gal � 9/2. Vrai.
9/4 * 2 = 18/4 = 9 / 2..
Le carr� de 3 fois racine carr�e (5) est �gal � 15. Faux.
(3 fois racine carr�e (5))2 = 32*5 =45.
Pour tous les nombres x, on a (2x +3)2 = 9+2x(2x +3). Faux.
(2x +3)2 =4x2+9+12x ; 9+2x(2x +3) =4x2+9+6x.

On consid�re le programme de calcul suivant :
• Choisir un nombre
• Ajouter 5
• Prendre le carr� de cette somme
 Quel r�sultat obtient-on lorsqu’on choisit le nombre 3 ? le nombre −7 ?
Carr� de (3+5) = (3+5)2 =64 ; carr� de (-7+5) = (-7+5)2 =4.
Quel nombre peut-on choisir pour obtenir 25 ?
Carr� de (x+5) = (x+5)2 =25 = (�5)2 ; x+5 = �5 ; x=0 ou x = -10.
Peut-on obtenir −25 ? Justifier la r�ponse.
Non, un carr� est toujours positif ou nul.
On appelle f la fonction qui, au nombre choisi, associe le r�sultat du programme de calcul.
 Parmi les fonctions suivantes, quelle est la fonction f ?
f(x) = x2+25 ; f(x) =(x+5)2 ; f(x)= x2+5 ; f(x) =2(x+5).
 Est-il vrai que −2 est un ant�c�dent de 9 ?
 (x+5)2 =9 = (�3)2 ; x+5 = �3 ; x=-2 ou x = -8.
 R�soudre l’�quation (x +5)2= 25.
 x+5 = �5 ; x=0 ou x = -10.
En d�duire tous les nombres que l’on peut choisir pour obtenir 25 � ce programme de calcul.
On peut choisir 0 ou -10.




Une ville de 50 000 habitants d�pense 10 euros par mois et par habitant pour faire traiter les poubelles m�nag�res.
Quel est le budget sur une ann�e de cette ville pour faire traiter les poubelles ? Justifier la r�ponse.
50 000*10 *12 = 6,0 106 €

Voici un article trouv� sur internet.
D’apr�s l’Observatoire des Usages Internet deM�diam�trie, au dernier trimestre 2011, 28 millions d’internautes  ont achet� en ligne. Au premier trimestre de 2012, on constate une augmentation de 11% du nombre d’achats en ligne.
En utilisant les donn�es de cet article, calculer le nombre de cyberacheteurs au premier trimestre 2012. Arrondir le r�sultat � 0,1million pr�s.
28 106 *1,11 =3,108 107 = 31,08 106 ~31,1 106.
Si la progression sur le deuxi�me trimestre 2012 est, elle aussi, de 11%, quelle serait la progression en pourcentage sur les deux trimestres ? Justifier la r�ponse.
1,11*1,11 = 1,112 =1,2321 soit environ 23,2 %.

Quelles sont les solutions de l'�quation (x+7)(2x-7)=0 ?
x+7=0 conduit � x = -7 et 2x-7=0 conduit � x = 7/2 = 3,5.
Quelles sont les solutions de l'in�quation -2(x+7) <= -16 ?
2(x+7) < =16 ; x+7 <  =8 ; x< =1.
Quelle est la forme d�velopp�e de (7x-5)2 ?
49x2+25-70x.
 Quelle est la forme factoris�e de 9-64x2 ?
32-(8x)2=(3-8x)(3+8x).
Quelle est la nature de la section gris�e ?
E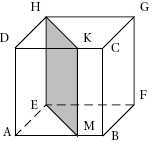H = c�t� du cube =a ; HK est g�n�ralement diff�rente du c�t� du cube ; le carr� est donc exclu.
Ce quadrilat�re poss�de des c�t�s oppos�s parall�les et 4 angles droits : il s'agit donc d'un rectangle.



Une salle contient des  tables � 3 pieds et � 4 pieds. L�a compte les yeux band�s et trouve 169 pieds. Son fr�re lui indique qu'il y a 34 tables � 4 pieds. Sans enlever son bandeau, elle parvient � donner le nombre de tables de 3 pieds, qui est  a 135 ; b) 11 ; c) 166.
Les tables � 4 pieds poss�dent 34*4 = 136 pieds ; les tables � 3 pieds compte 169-136 = 33 pides soit 333 = 11 tables.

90% d'un iceberg est situ� sous la surface de l'eau. La hauteur totale d'un iceberg dont la partie visible est 35 m est environ : 350 m ; 3500 m ; 31,5 m.
La  partie visible repr�sente 10 % de l'iceberg ; hauteur totale = hauteur visible / 0,1 = 35/0,1 = 350 m.

Arthur poss�de 21 billets. Il a des billets de 5 € et des billets de 10 €. pour un total de 125 €. Combien de billets de chaque sorte pos�de t-il ?
On note x le nombre de billets de 5 € et 21-x le nombre de billets de 10 €.
5x +(21-x) 10 = 125 ; 5x +210 -10 x = 125 ; 5 x = 210-125 = 85 ; x = 17.
17 billets de 5 € et 4 billets de 10 €.

Flavien veut r�partir la totalit� de 760 drag�es au chocolat et 1045 drag�es aux amandes dans des sachets ayant la m�me r�partition de drag�es au chocolat et aux amandes.
Peut-il faire 76 sachets ? Justifier.
Non : 760/76 = 10 ; 1045 / 76 = 13,75 ; nombre non entier.
Quel nombre maximal de paquets peut-il r�aliser et quelle est la composition de chaque paquet ?
760 = 23*5*19 ; 1045 =5*11*19 ; PGCD(760 ; 1045) = 5*19 = 95.
Il peut r�aliser au maximum 95 paquets contenant 8 drag�es au chocolat et 11 drag�es aux amandes.

Tom doit calculer 3,52. Julie lui dit :" effectue le produit 3 par 4 et ajoute 0,25".
Julie a-t-elle raison ?
3,5*3,5 =12,25 ; 3*4 +0,25=12,25.
Ptoposer une fa�on simple de calculer 7,52 et donner le r�sultat.
7,52 = 7*8+0,25 = 56,25.
Julie propose la conjecture suivante (n+0,5)2 = n(n+1)+0,25 avec n entier positif. Prouver que ela est vrai.
(n+0,5)2 =n2 +n +0,25 = n(n+1) +0,25.

menu