Lire et utiliser un graphe, fonction affine, parabole, brevet 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . (sujet 2013) Avec un logiciel : on a construit un carré ABCD, de côté 4 cm ; on a placé un point M mobile sur [AB] et construit le carré MNPQ comme visualisé ci-dessous. On a représenté l'aire du carré MNPQ en fonction de la longueur AM. 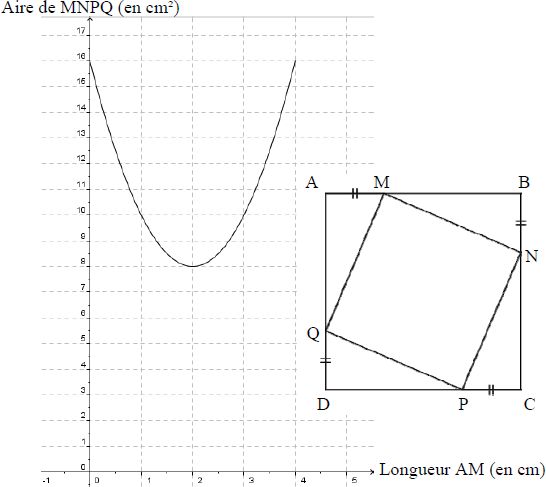En utilisant ce graphique répondre aux questions suivantes. Aucune justification n’est attendue.  Déterminer pour quelle(s) valeur(s) de AM, l’aire de MNPQ est égale à 10 cm2. Déterminer l’aire de MNPQ lorsque AM est égale à 0,5 cm. Pour quelle valeur de AM l’aire de MNPQ est-elle minimale ? Quelle est alors cette aire ? 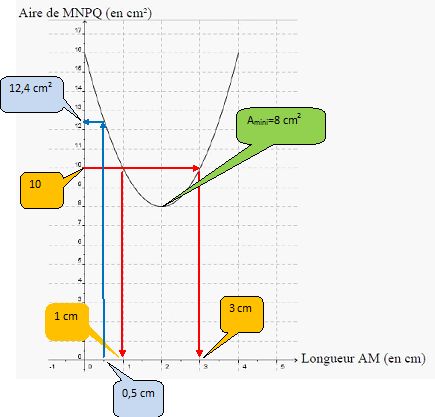L'aire est minimale et vaut 8 cm2 pour AM = 2 cm. . . On a utilisé un tableur pour calculer les images de différentes valeurs de x par une fonction affine f et par une autre fonction g. Une copie de l’écran obtenu est donnée ci-dessous. Quelle est l’image de -3 par f ? L'image de 3 par f est -8. Calculer f (7). f(7) = -5 x 7+7 =28. Donner l’expression de f (x). f(x) = -5 x +7. On sait que g (x) = x² + 4. Une formule a été saisie dans la cellule B3 et recopiée ensuite vers la droite pour compléter la plage de cellules C3: H3. Quelle est cette formule ? =B1*B1+4 . Le débit d’une connexion internet varie en fonction de la distance du modem par rapport au central téléphonique le plus proche. On a représenté ci-dessous la fonction qui, à la distance du modem au central téléphonique (en kilomètres), associe son débit théorique (enmégabits par seconde). Marie habite à 2,5 km d’un central téléphonique. Quel débit de connexion obtient-elle ? Paul obtient un débit de 20 Mbits/s. À quelle distance du central téléphonique habite-t-il ? Pour pouvoir recevoir la télévision par internet, le débit doit être au moins de 15Mbits/s. À quelle distance maximum du central doit-on habiter pour pouvoir recevoir la télévision par internet ? Pour cet exercice, on utilise uniquement la courbe donnée ci-dessous qui représente une fonction . Donne une valeur approchée de f (2). Donne l'(ou les) antécédent($ de 5 par la fonction. Place sur la courbe de la fonction , un point S qui te semble avoir la plus petite ordonnée. Par lecture graphique, donne des valeurs approchées des coordonnées de ton point S. Pour un prix x compris entre 0 et 20 (, le nombre d’abonnés est donné par la fonction A telle que : A(x) = −50x +1250. La recette, c’est-à-dire le montant perçu par l’éditeur de cette revue, est donnée par la fonction R telle que : R(x) = −50x2 +1250x. 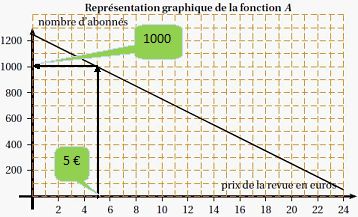Le nombre d’abonnés est-il proportionnel au prix de la revue ? Justifier. Vérifier, par le calcul, que A(10) = 750 et interpréter concrètement ce résultat. Le graphe est une droite ne passant pas par l'origine. Le nombre d'abonnés n'est pas proportionnel au prix de la revue. Le prix de la revue diminue quand le nombre d'abonnés croît. A(10)=-50*10+1250= 750.750 abonnés payent 10 € la revue. La fonction R est-elle affine ? Justifier. Le graphe n'est pas une droite : la fonction R n'est pas affine. Déterminer graphiquement pour quel prix la recette de l’éditeur est maximale. Déterminer graphiquement les antécédents de 6 800 par R. Lorsque la revue coûte 5 euros, déterminer le nombre d’abonnés et la recette. .

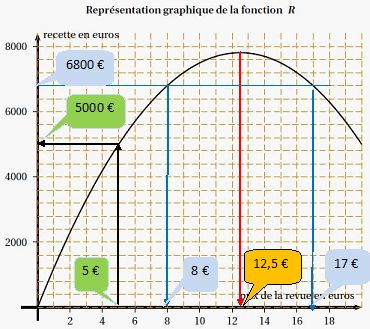
menu