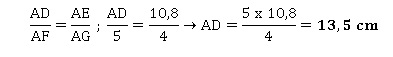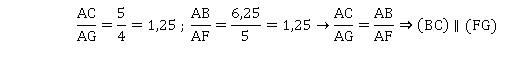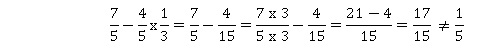Mathématiques, Diplome national du brevet, Métropole septembre 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Probabilités. 6 points. Un sac opaque contient 120 boules toutes indiscernables au toucher, dont 30 sont bleues. Les autres boules sont rouges ou vertes. On considère l’expérience aléatoire suivante : On tire une boule au hasard, on regarde sa couleur, on repose la boule dans le sac et on mélange. 1. Quelle est la probabilité de tirer une boule bleue ? Écrire le résultat sous la forme d’une fraction irréductible. 30 boules bleues sur 120 boules. La probabilité de tirer une boule bleue est égale à : 30 / 120 = 3 / 12 = 1 /4. 2. Cécile a effectué 20 fois cette expérience aléatoire et elle a obtenu 8 fois une boule verte. Choisir, parmi les réponses suivantes, le nombre de boules vertes contenues dans le sac (aucune justification n’est demandée) : a. 48 ; b. 70 ; c. On ne peut pas savoir ; d. 25. Cécile tire une boule et la remet dans le sac ; elle peut tirer plusieurs fois la même boule verte. On ne peut pas connaître le nombre de boules vertes. 3. La probabilité de tirer une boule rouge est égale à 0,4. a. Quel est le nombre de boules rouges dans le sac ? 0,4 = nombre de boules rouges / 120 ; nombre de boules rouges = 120 x0,4 = 48. b. Quelle est la probabilité de tirer une boule verte ? Le sac contient 30 bleues et 48 rouges ; il contient donc 120 -30-48 =42 boules vertes. Probabilité de tirer une boule verte : 42 / 120 = 7 / 20 = 0,35. . . Thalès, Pythagore. 7 points. La figure ci-dessous a été faite à la main. 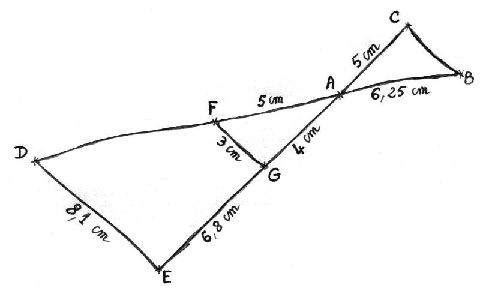Les points D, F, A et B sont alignés, ainsi que les points E, G, A et C. De plus, les droites (DE) et (FG) sont parallèles. 1. Montrer que le triangle AFG est un triangle rectangle. AF2 = 52 = 25 ; FG2 +AG2 = 32 +42 = 25. AF2 =FG2 +AG2  ; d'après la réciproque du théorème de Pythagore, le triangle AFG est rectangle en G. 2. Calculer la longueur du segment [AD]. En déduire la longueur du segment [FD]. 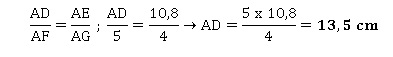[FD]=[AD]-[AF]=13,5 -5 = 8,5 cm. 3. Les droites (FG) et (BC) sont-elles parallèles ? Justifier. 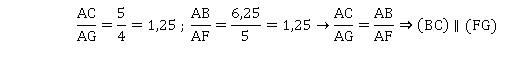Réciproque du théorème de Thalès. . . Exercice 3. 6 points. Voici trois figures différentes, aucune n’est à l’échelle indiquée dans l’exercice. 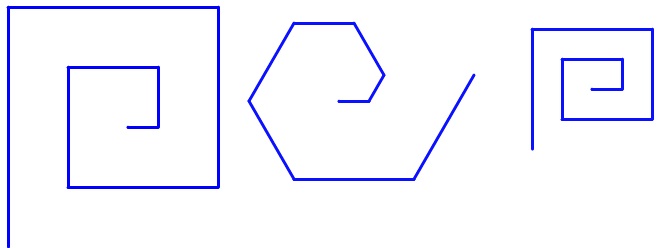Le programme ci-dessous contient une variable nommée « longueur ». Quand le drapeau est cliqué Cacher Aller à x=0 ; y=0 S'orienter à 90° vers la droite. Mettre longueur à 30. Effacer tout. Mettre la taille du stylo à 3. Stylo en position écriture. Répéter deux fois.   un tour                        ajouter à longueur 30 Le bloc : un tour Définir un tour Répéter deux fois Avancer de longueur Tourner de 90° dans le sens anti-horaire. Fin répéter. Ajouter à longueur 30. Répéter deux fois. Avancer de longueur. Tourner de 90° dans le sens anti-horaire. Fin répéter 1. a. Dessiner la figure obtenue avec le bloc « un tour » donné dans le cadre de droite ci-dessus, pour une longueur de départ égale à 30, étant orienté vers la droite avec le stylo, en début de tracé. On prendra 1 cm pour 30 unités de longueur, c’est-à-dire 30 pixels. 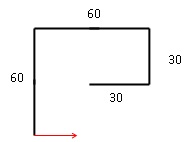b. Comment est-on orienté avec le stylo après ce tracé ? (aucune justification n’est demandée) Le stylo est orienté vers la droite. 2. Laquelle des figures 1 ou 3 le programme ci-dessus permet-il d’obtenir ? Justifier votre réponse. La figure de gauche ne correspond pas, car les deux premiers segments n'ont pas la même longueur. La figure centrale ne convient pas, la rotation est de 45° et non pas de 90°. La figure de droite convient : on a deux segments de longueur 30, puis deux de longueur 60, puis deux de longueur 90 et enfin deux de longueur 120. 3. Quelle modification faut-il apporter au bloc « un tour » pour obtenir la figure du centre ci-dessus ? Il faut effectuer une rotation de 45° dans le sens anti-horaire à la place d'une rotation de 90°. Exercice 4. 9 points. Monsieur Chapuis souhaite changer le carrelage et les plinthes(*) dans le salon de son appartement. Pour cela il doit acheter des carreaux, de la colle et des plinthes en bois qui seront clouées. Il dispose des documents suivants : Document 1 : plan , la pièce correspond à la partie grisée. 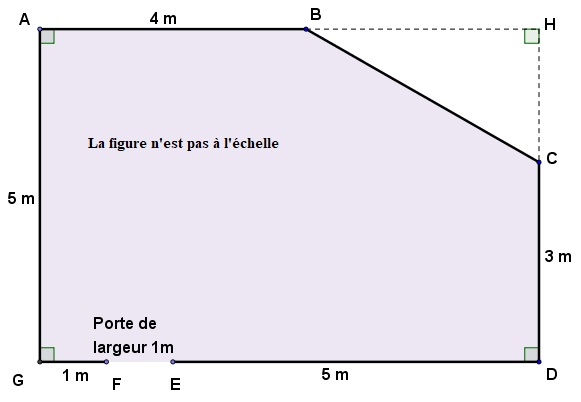1. a. En remarquant que la longueur GD est égale à 7 m, déterminer l’aire du triangle BCH. BH x HC / 2 = 3 x2 / 2 = 3 m2. b. Montrer que l’aire de la pièce est 32 m2. Aire du rectangle AHDG - aire du triangle BCH= 7 x5 -3 =32 m2. 2. Pour ne pas manquer de carrelage ni de colle, le vendeur conseille à monsieur Chapuis de prévoir une aire supérieure de 10 % à l’aire calculée à la question 1. Monsieur Chapuis doit acheter des boîtes entières et des sacs entiers. Déterminer le nombre de boîtes de carrelage et le nombre de sacs de colle à acheter. 32 x1,1 =35,2 m2. Un sac de colle permet de coller 4 m2, il faut donc 9 sacs. Une boîte de carreaux permet de couvrir 1,25 m2, donc il faut 35,2 / 1,25 ~28 boîtes. 3. Le vendeur recommande aussi de prendre une marge de 10% sur la longueur des plinthes. Déterminer le nombre total de plinthes que monsieur Chapuis doit acheter pour faire le tour de la pièce. On précise qu’il n’y a pas de plinthe sur la porte. BC2 =BH2 + HC2 =32+22=13  ; BC ~3,6 m. Longueur des plintes :5 +1 +5 +4 +3 +3,6 = 21,6 m. Puis prendre en compte la marge : 21,6 x1,1 ~23,8 m. Longueur d'une plinthe : 1m ; il faut donc 24 plinthes. 4. Quel est le montant de la dépense de monsieur Chapuis, sachant qu’il peut se contenter d’un paquet de clous ? Arrondir la réponse à l’euro près. Carrelage 19,95 €  la boîte soit 19,95 x28 =558,6 € Colle, 22 € le sac soit 22 x9 = 198 €. Plinthe, 2,95 € le mètre, soit 2,95 x24 =70,8 €. Clous, 5,50 €. Total : 832,9 €. Exercice 5. 5 points Pour chaque affirmation, dire en justifiant, si elle est vraie ou fausse. Affirmation 1 : Le résultat du programme de calcul suivant est toujours égal à 6. Vrai. Choisir un nombre Ajouter 3 Multiplier le résultat par 2 Soustraire le double du nombre de départ. Soit N le nombre choisi. (N+3 )x2 -2N = 2N+6-2N = 6. Affirmation 2 : Le résultat du calcul suivant est égal à 1 / 5 . Faux. 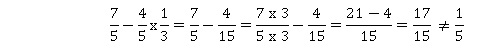Affirmation 3 : La solution de l’équation 4x−5 = x+1 est une solution de l’équation x2-2x=0. Vrai. 4x-x =1+5 ; 3x = 6 ; x = 2. x2-2x=0 ; x ( x-2)=0, solution zéro et 2. Affirmation 4 : Pour tous les nombres entiers n compris entre 2 et 9, 2n−1 est un nombre premier. Faux. n= 2 ; 2n-1 = 3 ; n=3 ; 2n-1 = 5 ; n = 4 ; 2n-1 = 15, ce nombre n'est pas premier ( 15 est divisible par 3 et 5). Exercice 6. 5 points. Dans une station de ski, les responsables doivent enneiger la piste de slalom avec de la neige artificielle. La neige artificielle est produite à l’aide de canons à neige. La piste est modélisée par un rectangle dont la largeur est 25 m et la longueur est 480 m. Chaque canon à neige utilise 1 m3 d’eau pour produire 2 m3 de neige. Débit de production de neige : 30 m3 par heure et par canon. 1. Pour préparer correctement la piste de slalom, on souhaite produire une couche de neige artificielle de 40 cm d’épaisseur. Quel volume de neige doit-on produire ? Quel sera le volume d’eau utilisé ? Volume de neige : 25 x 480 x 0,40 =4800 m3 soit 2400 m3 d'eau. 2. Sur cette piste de ski, il y a 7 canons à neige qui produisent tous le même volume de neige. Déterminer la durée nécessaire de fonctionnement des canons à neige pour produire les 4 800 m3 de neige souhaités. Donner le résultat à l’heure près. Chaque canon produit 4800 / 7~686 m3 de neige. Durée : 686 / 30 ~23 heures. Exercice 7. 7 points. Les légionelles sont des bactéries présentes dans l’eau potable. Lorsque la température de l’eau est comprise entre 30°C et 45°C, ces bactéries prolifèrent et peuvent atteindre, en 2 ou 3 jours, des concentrations dangereuses pour l’homme. On rappelle que « μm » est l’abréviation de micromètre. Un micromètre est égal à un millionième de mètre. 1. La taille d’une bactérie légionelle est 0,8 µm. Exprimer cette taille en m et donner le résultat sous la forme d’une écriture scientifique. 0,8 x 10-6 = 8 x10-7 m. 2. Lorsque la température de l’eau est 37°C, cette population de bactéries légionelles double tous les quarts d’heure. Une population de 100 bactéries légionelles est placée dans ces conditions. On a créé la feuille de calcul suivante qui permet de donner le nombre de bactéries légionelles en fonction du nombre de quarts d’heure écoulés : A B 1 Nombre de quart d'heure Nombre de bactéries 2 0 100 3 1 200 4 2 400 5 3 800 6 4 1600 7 5 3200 8 6 6400 9 7 12800 a. Dans la cellule B3, on veut saisir une formule que l’on pourra étirer vers le bas dans la colonne B pour calculer le nombre de bactéries légionelles correspondant au nombre de quarts d’heure écoulés. Quelle est cette formule ? =B2*2 b. Quel est le nombre de bactéries légionelles au bout d’une heure ? 100 x 23 = 800. c. Le nombre de bactéries légionelles est-il proportionnel au temps écoulé ? Non, le nombre de bactéries est égal à 100 x2n-1, avec n le nombre de quart d'heure. Cette relation n'est pas linéaire. D'après le tableau, le nombre de bactéries n'est pas proportionnel au nombre de quart d'heure. d. Après combien de quarts d’heure cette population dépasse-t-elle dix mille bactéries légionelles ? Voir tableau ci-dessus. 3. On souhaite tester l’efficacité d’un antibiotique pour lutter contre la bactérie légionelle. On introduit l’antibiotique dans un récipient qui contient 104 bactéries légionelles au temps t = 0. La représentation graphique suivante, donne le nombre de bactéries dans le récipient en fonction du temps. a. Au bout de 3 heures, combien reste-t-il environ de bactéries légionelles dans le récipient ? b. Au bout de combien de temps environ reste-t-il 6000 bactéries légionelles dans le récipient ? 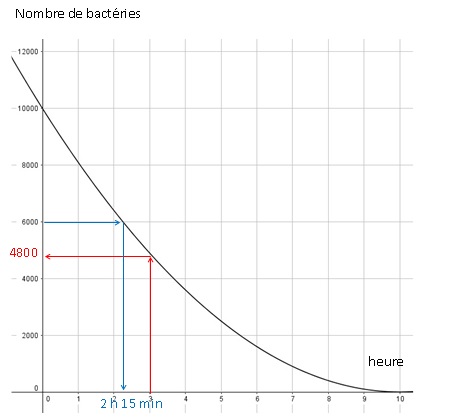c. On estime qu’un antibiotique sera efficace sur l’être humain s’il parvient à réduire de 80% le nombre initial de bactéries dans le récipient en moins de 5 heures. En s’aidant du graphique, étudier l’efficacité de l’antibiotique testé sur l’être humain. Il doit rester 104 x0,2 = 2 103 bactéries au bout de 5 heures pour un antibiotique efficace. D'après le graphe il reste plus de 2000 bactéries au bout de 5 heures. Cet antibiotique manque d'efficacité.

menu