Mathématiques,
Brevet Asie 2017.
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1 (4 points).
Aux États-Unis, la température se mesure en degré
Fahrenheit (en °F).
En France, elle se mesure en degré Celsius (en °C).
Pour faire les conversions d'une unité à l'autre, on a utilisé un
tableur.
|
A
|
B
|
1
|
Conversions
|
2
|
Températures
en °C
|
Températures
en °F
|
3
|
-5
|
23
|
4
|
0
|
32
|
5
|
5
|
41
|
6
|
10
|
50
|
7
|
15
|
59
|
8
|
20
|
68
|
9
|
25
|
77
|
1. Quelle
température en °F correspond à une température de 20°C ?
68 °F.
2. Quelle
température en °C correspond une température de 41 °F ?
5°C.
3. Pour convertir
la température de °C en °F, il faut multiplier la température en °C par
1,8 puis ajouter 32. On a écrit une formule en B3 puis on l'a recopiée
vers le bas.
Quelle formule a-t-on pu saisir dans la cellule B3 ?
=A3*1,8+32
Exercice 2 (5 points)
Dans une classe de 24 élèves, il y a 16 filles.
1) L un des deux
diagrammes ci-dessous peut-il représenter correctement la répartition
des élèves de cette clsse ?
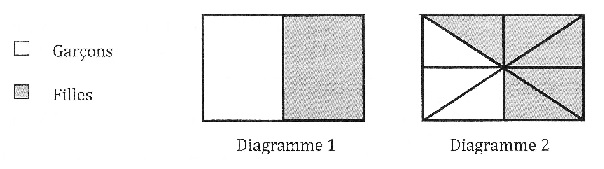
Le diagramme 1 ne
convient pas : il indique qu'il y a autant de filles que de garççons.
Le diagramme 2 indique qu'il y a 24 x5 / 8 = 15 filles et 24 x3 / 8 = 9
garçons.
Il ne convient pas.
2) 0n a représenté
Ia répartition des élèves de cette classe par un diagramme circulaire.
circulaire.
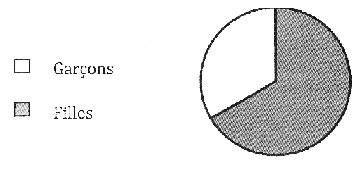
Écrire le calcul permettant de déterminer la mesure de I'angle du
secteur qui représente
les garçons.
Il y a 8 garçons et 16 filles. Il y a deux fois plus de filles que de
garçons. les filles représentent les 2/ 3 de la classe et les garçons
seulement 1 /3.
Mesure de l'angle du secteur qui représente les garçons : 360 x 8
/ 24 = 360 / 3 = 120°.
|
....
.....
|
Exercice 3 (6 points)
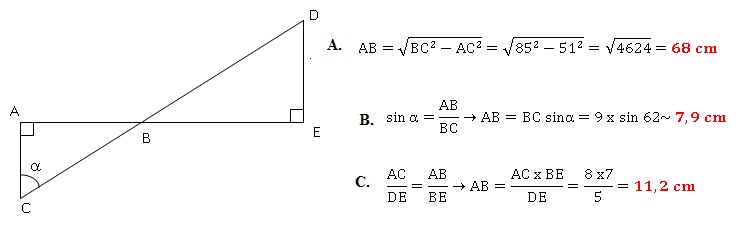
On considère la figure ci-dessous qui n'est pas représentée en waie
grandeur.
Les points A, B et E sont alignés ainsi que les points C, B et D.
Calculer AB dans les trois
cas A, B, C.
Exercice 4 ( 4
points).
Margot a écrit le programme suivant. Il permet de dessiner avec trois
touches du clavier.
Quand le drapeau est cliqué
Initialisation ( le dessin précédent est effacé, le stylo est
relevé et placé à gauche de l'écran ).
Quand flèche haut est cliqué
S'orienter à 0°.
Stylo en position d'écriture.
Avancer de 50.
Relever le stylo.
Quand flèche droite est cliqué.
S'orienter à 90° ( tourner
de 90° dans le sens des aiguilles d'une montre ).
Stylo en position d'écriture.
Avancer de 50.
Relever le stylo.
Quand
flèche bas est cliqué.
S'orienter à 180° ( tourner
de 180° dans le sens des aiguilles d'une montre ).
Stylo en position d'écriture.
Avancer de 50.
Relever le stylo.
1. Parmi les trois dessins suivants,
un seul ne pourra pas être réalisé avec ce programme. Lequel ?
Expliquer.
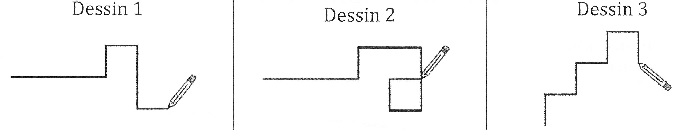
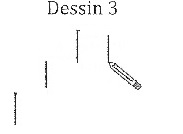
Dessin 1 :
flèche droite ; flèche droite ; flèche droite ; flèche haut ; flèche
droite ; flèche bas ; flèche bas ; flèche droite.
Dessin
2 : flèche
droite ; flèche droite ; flèche droite ; flèche haut ; flèche droite ;
flèche droite ; flèche bas ; flèche bas ; il faudrait une instruction
flèche gauche pour continuer à dessiner.
Dessin 3 ; flèche haut ; flèche droite
; flèche haut ; flèche droite
; flèche haut ; flèche droite
; flèche bas.
|
|
|
|
2. |ulie a modifié le programme de
Margot [voir ci-dessous). Que devient alors le dessin 3 avec le
programme modifié par Julie ?
Quand le drapeau est cliqué
Initialisation ( le dessin précédent est effacé, le stylo est
relevé et placé à gauche de l'écran ).
Quand flèche haut est cliqué
S'orienter à 0°.
Stylo en position d'écriture.
Avancer de 50.
Relever le stylo.
Quand flèche droite est cliqué.
S'orienter à 90° ( tourner
de 90° dans le sens des aiguilles d'une montre ).
Avancer de 50.
Quand
flèche bas est cliqué.
S'orienter à 180° ( tourner
de 180° dans le sens des aiguilles d'une montre ).
Stylo en position d'écriture.
Avancer de 50.
Relever le stylo.
|
|
|
|
Exercice
5 (8 points)
Pour mesurer les précipitaüons, Météo France utilise deux sortes de
pluviomètres :
- des pluviomètres à lecture directe ;
- des pluviomètres électroniques.
La mesure des précipitations s'exprime en millimètre. On donne
ainsi Ia hauteur d'e au H qui
est tombée en utilisant la formule :
H = V / S où V est
le volume d'eau tombée sur une surface S.
Pour H exprimée en mm , V est exprimé en mm3 et.S en mm2.
Partie I :
Pluviomètres à lecture directe.
Ces pluviomètres sont composés d'un cylindre de réception et d'un
réservoir conique gradué.
1) Vérifier à
l'aide de la formule que lorsqu'il est tombé 1 mm de pluie, cela
correspond à 1 L d'eau tombée sur une surface de 1 m2.
V = 1 L = 1 dm3 = 106 mm3. S = 1
m2 = 106 mm2. H = 106 / 106
= 1 mm.
2) Un plurfiomètre
indique 10 mm de pluie. La surface qui reçoit la pluie est de 0,01 m2.
Quel est le volume d'eau dans ce pluviomètre ?
V = H S avec S = 0,01 x 106 = 104 mm2.
V = 10 x 104 =105 mm3 = 0,1 x106
mm3 = 0,1 dm3 = 0,1 L.
Ou bien : 10 L reçus sur 1 m2, soit 0,1 L reçu sur 0,01 m2.
Partie II :
Pluviomètres électroniques.
Durant un épisode pluvieux, on a obtenu le graphique suivant grâce à un
pluviomètre électronique :
Hauteur d'eau mesurée en fonction du temps écoulé.
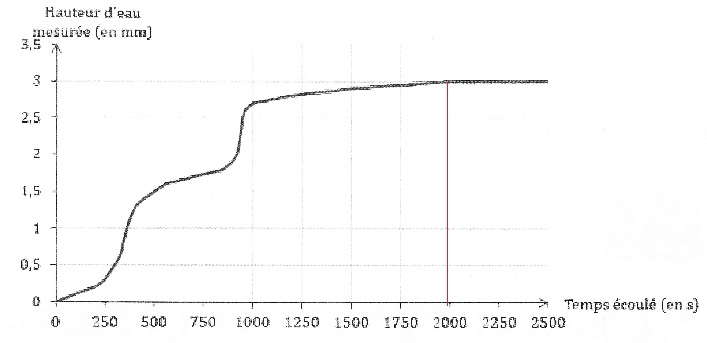
1) L'épisode
pluvieux a commencé à 1,7h15. Vers quelle heure la pluie s'est-elle
arrêtée?
La pluie s'est arrêtée quand la hauteur d'eau reste constante, soit
environ 2000 s après 17 h15.
2000 s ou 2000 / 60 ~ 33 min ; 17 h 15 +33 min = 17 h 48 min.
2. Cette pluie
serait-elle qualifié de faible, modérée ou forte ?
3 mm sont tombés durant environ 0,5 heure, soit 6 mm par heure.
Cette valeur étant comprise entre 2,6 et 7,5 mm /h, cette pluie est
qualifiée de modérée.
Exercice 6 (7 noints)
Gaspard réalise des motifs avec des carreaux de mosaïque blancs et gris
de la façon suivante.
Gaspard forme un carré avec des carueaux gris puis le borde avec
des carreaux blancs.
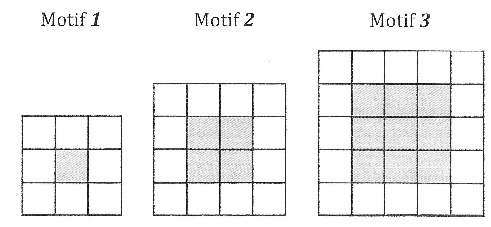
1) Combien de
carreaux blancs Gaspard va-t-il utiliser pour border le carré gris du
mofif 4 (un carré ayant 4 carreaux gris de côté) ?
Motif 1 : 1 gris et 8 blancs soit 2 x(nombre de gris par rangée+2) +2 x
nombre de gris par rangée.
Motif 2 : 4 = 22 gris et 12 blancs soit 2x (nombre de gris
par rangée+2) +2 x nombre de gris par rangée.
Motif 3 : 9= 32 gris et 16 blancs 2x (nombre de gris par
rangée +2) +2 x nombre de gris par rangée.
Motif 4 : 16= 42 gris et 20 blancs.
2) a) justifier que
Gaspard peut réaliser un motif de ce tÿpe en utilisant exactement 144
carreaux gris.
144 est égal au carré d'un nombre entier : 122 = 144.
b) Combien de
carreaux blancs utilisera-t-il alors pour border le carré gris obtenu ?
2x (nombre de gris par rangée +2) +2 x nombre de gris par
rangée=2x(12+2) +2x12 = 28+24=52.
3) On appelle «
motif n » le motif pour lequel on borde un carré de n carreaux gris de
côté,
Trois élèves ont proposé chacun une expression pour calculer le nombre
de carreaux blancs nécessaires pour réaliser Ie « motif n » :
- Expression n°1 : 2xn+2x (n+2)
- Expression n°2 : 4x(n+2)
- Expression n°3 : 4x(n+2) - 4
Une seule de ces trois expressions ne convient pas. Laquelle ?
2 x(n+2) +2 xn = 4 xn+4 = 4x(n+2)-4.
L'expression 2 ne convient pas.
|
Exercice 7 (6 noints)
L'entraîneur d'un club d'athlétisme a relevé les performances de ses
lanceuses de poids sur cinq lancers. Voici une partie des relevés qu'il
a effectués (il manque trois
performances pour une des lanceuses) :
|
Lancers
|
n°1
|
n°2
|
n°3
|
n°4
|
n°5
|
Moyenne
|
Etendue
|
Médiane
|
Performances
( en m)
|
Solenne
|
17,8
|
17,9
|
18
|
19,9
|
17,4
|
18,2
|
2,5
|
17,9
|
Racchida
|
17,9
|
17,6
|
18,5
|
18
|
19
|
18,2
|
1,4
|
18
|
Sarah
|
18
|
?
|
19,5
|
?
|
?
|
|
|
|
On
connaît les caractéristiques de l'une des lanceuses :
Caractéristiques des cinq lancers : étendue : 2,5 m ; moyenne : 18,2 m
; médiane : 18 m.
1) Expliquer
pourquoi ces caractéristiques ne concernent ni les résultats de
Solenne, ni ceux de Rachida.
Solenne : la médiane ne convient pas ; Rachida : l'étendue ne convient
pas.
2) Les
caractéristiques données sont donc celles de Sarah. Son meilleur lancer
est de 19,5 m. Quels peuvent être les trois lancers manquants de Sarah ?
19,5 -2,5 = 17 m, lancer le plus court.
Un lancer est compris entre 17 et 18 m ; un autre est compris
entre 18 et 19,5 m.
On note x et y les deux lancers inconnus : (18 +17 +19,5 +x +y) / 5 =
18,2 soit x +y +54,5 = 18,2 x5 = 91 ; x+y = 91-54,5 = 36,5.
17 et 19,5 m ; 17,1 et 19,4 m ; 17,2 et 19,3 m ; 17,3 et 19,2 m ; 17,4
et 19,1 m ; 17,5 et 19 m ; 17,6 et 18,9 m ; 17,7 et 18,8 m ; 17,8
et 18,7 m ; 17,9 et 18,6 m ; 18 et 18,5 m.
Exercice 8 (5
points)
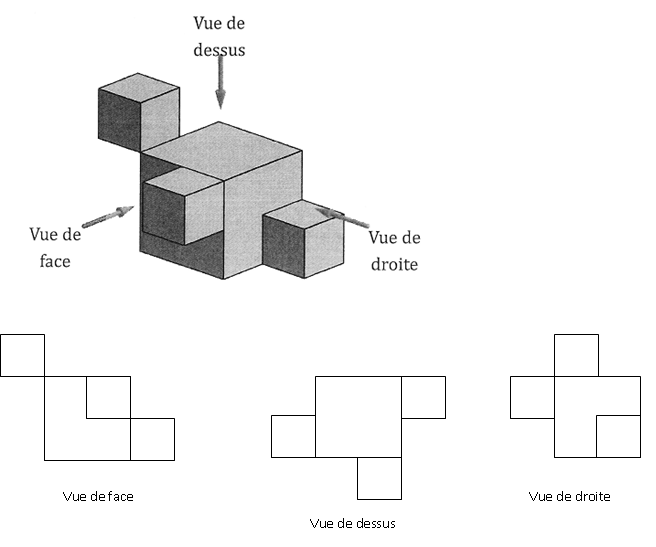
La figure ci-dessous représente un solide constitué de l'assemblage de
quatre cubes : - trois cubes d'arête 2 cm ; - un cube d'arête 4 cm.
1) Quel est le
volume de ce solide ?
3 x23 +43=24 +64 = 88 cm3.
2) on a dessiné
deux vues de ce solide face (elles ne sont pas en vraie grandeur ).
Dessiner la vue de droite de ce solide en vraie grandeur.
|
|