Mathématiques,
Brevet des collèges annales zéro 2017
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Mathématiques. Exercice 1.
Pour chacune des affirmations suivantes, dire si elle est vraie ou
fausse en justifiant soigneusement la réponse.
1) Un sac contient 6 jetons rouges,
2 jetons jaunes et des jetons verts. La probabilité de tirer un jeton vert vaut
0,5.
Affirmation : le sac
contient 4 jetons verts. Faux.
Nombre total de jetons N.
Probabilité de tirer un jeton rouge ou jaune = 0,5 = nombre de jetons
rouge et jaune / N.
N = (6+2) / 0,5 = 16 dont 8 jetons verts.
2) En informatique, on utilise comme
unités de mesure les multiples suivants de l’octet :
1Ko = 103
octets, 1Mo = 106 octets, 1 Go = 109 octets, 1To
= 1012 octets, où
Ko est l’abréviation de kilooctet, Mo celle de mégaoctet, Go celle de
gigaoctet, To celle de téraoctet.
On partage un disque dur
de 1,5 To en dossiers de 60 Go chacun.
Affirmation : on obtient
ainsi 25 dossiers. Vrai.
1,5 103 / 60=25.
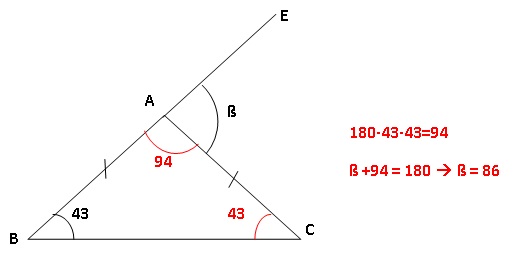
3) Sur la figure
codée suivante, les points B, A et E sont alignés.
Affirmation
: l’angle ß mesure 137°. Faux.
4) Un verre de
forme conique est complètement rempli.
On verse son contenu de sorte que la hauteur du liquide soit divisée
par 2.
Affirmation : le
volume du liquide est divisé par 6.
Faux.
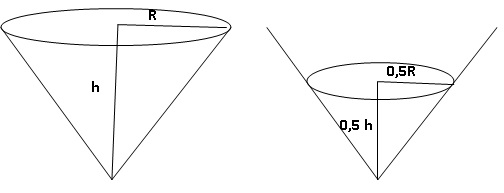
Volume du verre rempli =1/3 pR2
h ;
Si h est divisé par 2, R est également divisé par 2 ( Thalès).
Volume du verre rempli à mi-hauteur : 1/3
p(0,5R)2x0,5
h = 1/3
pR2
h / 8.
Exercice 2.
Le marnage désigne la
différence de hauteur entre la basse mer et la pleine mer qui suit.
On considère qu’à partir
du moment où la mer est basse, celle-ci monte de 1/12 du marnage
pendant la première heure, de 2/12 pendant la deuxième heure, de 3/12
pendant la troisième heure, de 3/12 pendant la quatrième heure, de 2/12
pendant la cinquième heure et de 1/12 pendant la sixième heure. Au
cours de chacune de ces heures, la montée de la mer est supposée
régulière.
1) À quel moment la montée de la mer
atteint-elle le quart du marnage ?
Au bout de la deuxième heure : 1/12 +2 /12 =3 /12 =1/4.
2) À quel moment la montée de la mer
atteint-elle le tiers du marnage ?
Au bout de ldeux heures 20 minutes : 1/12 +2 /12
+1 /12 =4 /12 =1/3.
Exercice 3.
Pour la fête d’un village on organise une course cycliste. Une prime
totale de 320 euros sera répartie entre les trois premiers coureurs. Le
premier touchera 70 euros de plus que le deuxième et le troisième
touchera 80 euros de moins que le deuxième. Déterminer la prime de
chacun des trois premiers coureurs.
On note x la prime
du second ; la prime du premier est : x+70 ; la prime du troisième est
: x-80.
x +x+70 +x-80 = 320 ; 3x = 320+10 = 330 ; x = 110.
110+70 = 180 € ; 110 € ; 110-80 = 30€.
Exercice 4.
Programme A 
Programme B 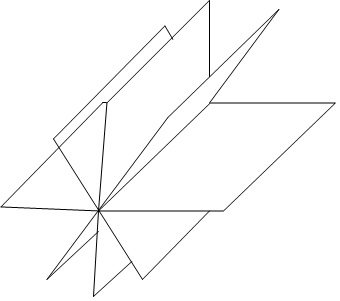
1) Pour
réaliser la figure ci-dessus, on a défini un motif en forme de losange
et on a utilisé l’un des deux programmes A et B ci-dessous. Déterminer
lequel et indiquer par une figure à main levée le résultat que l’on
obtiendrait avec l’autre programme.
|
|
|
Motif.
Stylo en position écriture
avancer de 40
tourner  de 45° de 45°
avancer
de 40
tourner  de 135° de 135°
avancer
de 40
tourner  de 45° de 45°
avancer de 40
tourner  de 135° de 135°
relever le stylo.
|
Programme A.
effacer tout
choisir la taille 1 pour le stylo
aller à x ;-230 y:0
s'orienter à 90°
répéter 8 fois
Motif
avancer de 55
|
Programme B.
effacer tout
choisir la taille 1 pour le stylo
aller à x :0 y:0
s'orienter à 90°
répéter 8 fois
Motif
tourner de 45°
|
2) Combien mesure l’espace entre
deux motifs successifs ? 55-40 = 15.
3) On souhaite
réaliser la figure ci-dessous :
Pour ce faire, on envisage d’insérer l’instruction " ajouter 1 à la
taille du stylo"
dans le programme utilisé à la question 1. Où faut-il insérer cette
instruction ?
répéter 8 fois
Motif
avancer de 55
ajouter 1 à la taille du stylo.
|
| ... |
|
|
Exercice 5.
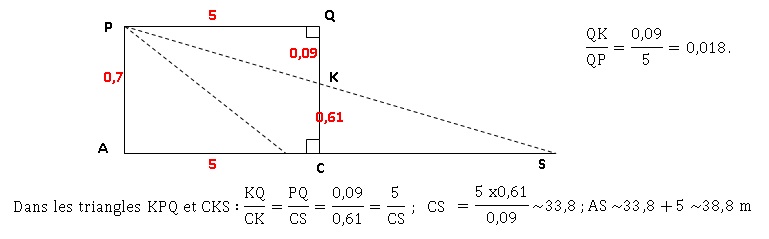
Pour
régler les feux de croisement d’une automobile, on la place face à un
mur vertical. Le phare, identifié au point P, émet un faisceau lumineux
dirigé vers le sol. On relève les mesures suivantes :
PA = 0,7 m, AC = QP = 5 m et CK = 0,61 m.
Sur le schéma ci-dessous, qui n’est pas à l’échelle, le point S
représente l’endroit où le rayon supérieur du faisceau rencontrerait le
sol en l’absence du mur. On considère que les feux de croisement sont
bien réglés si le rapport QK / QP est compris entre 0,015 et 0,02.
1) Vérifier que les
feux de croisement de la voiture sont bien réglés.
2) À quelle
distance maximale de la voiture un obstacle se trouvant sur la route
est-il éclairé par les feux de croisement ?
Exercice 6.
Un
panneau mural a pour dimensions 240 cm et 360 cm. On souhaite le
recouvrir avec des carreaux de forme carrée, tous de même taille, posés
bord à bord sans jointure.
1) Peut-on utiliser
des carreaux de : 10 cm de côté ? 14 cm de côté ? 18 cm de côté ?
On peut utiliser uniquement les carreaux de 10 cm de côtés :10 est un
diviseur de 240 et de 360 alors que 14 et 18 ne le sont pas.
2) Quelles sont
toutes les tailles possibles de carreaux comprises entre 10 et 20 cm ?
240 = 24 x3 x5 ; 360 =23 x32 x5.
10 cm ; 12 cm ; 15 cm ; 20 cm.
3) On choisit des
carreaux de 15 cm de côté. On pose une rangée de carreaux bleus sur le
pourtour et des carreaux blancs ailleurs. Combien de carreaux bleus
va-t-on utiliser ?
Sur chaque longueur on pose 360 / 15 = 24 carreaux.
Sur chaque largeur on pose ( 240-30) / 15 = 14 carreaux.
Total : 24 +24 +14 +14 = 76.
Exercice 7.
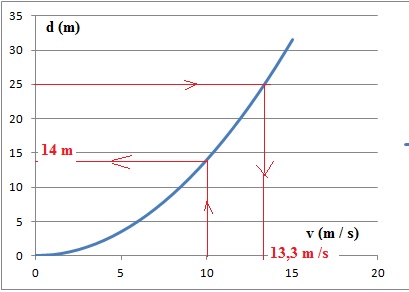
La distance de freinage d’un véhicule est la distance parcourue par
celui-ci entre le moment où le conducteur commence à freiner et celui
où le véhicule s’arrête. Celle-ci dépend de la vitesse du véhicule. La
courbe ci-dessous donne la distance de freinage d, exprimée en mètres,
en fonction de la vitesse v du véhicule, en m/s, sur une route mouillée.

1) Démontrer que 10
m/s = 36 km/h.
10 m parcourus en 1 s soit 10 x3600 = 36 000 m ou 36 km parcourus en
une heure.
2) a) D’après ce
graphique, la distance de freinage est-elle proportionnelle à la
vitesse du véhicule ?
Non, le graphe n'est pas une droite passant par l'origine.
b) Estimer la
distance de freinage d’une voiture roulant à la vitesse de 36 km/h. 14
m.
c) Un conducteur,
apercevant un obstacle, décide de freiner. On constate qu’il a parcouru
25 mètres entre le moment où il commence à freiner et celui où il
s’arrête. Déterminer, avec la précision permise par le graphique, la
vitesse à laquelle il roulait en m/s. 13,3 m /s.
3) On admet que la
distance de freinage d, en mètres, et la vitesse v, en m/s, sont liées
par la relation
d = 0,14 v2.
a) Retrouver par
le calcul le résultat obtenu à la question 2b.
d=0,14 x102= 14 m.
b) Un conducteur,
apercevant un obstacle, freine ; il lui faut 35 mètres pour s’arrêter.
À quelle vitesse roulait-il ?
v2 = d/0,14 = 35 / 0,14=250 ; v
~15,8 m/s.
|
|
|
|
Physique chimie.
Distance d’arrêt et distance de sécurité d’un véhicule.
Dr
est la distance de réaction. C’est la distance parcourue par le
véhicule entre le moment où le conducteur aperçoit l’obstacle et le
moment où il commence à freiner. Elle dépend de la durée de réaction du
conducteur.
Df est la distance de freinage. C’est la distance parcourue
par le véhicule entre le moment où le conducteur commence à freiner et
le moment où le véhicule s’arrête.
Da est la distance d’arrêt. C’est la distance parcourue par
le véhicule entre le moment où le conducteur aperçoit un obstacle et
l’arrêt du véhicule.
Le tableau suivant présente, pour différentes vitesses, la distance de
réaction et la distance de freinage sur route sèche d’un véhicule
correctement entretenu.
Vitesse
( km / h)
|
0
|
30
|
50
|
90
|
100
|
110
|
130
|
Vitesse
( m/s)
|
0
|
8
|
14
|
25
|
28
|
31
|
36
|
Dr
(m)
|
0
|
8
|
14
|
25
|
28
|
31
|
36
|
Df
(m)
|
0
|
6
|
16
|
50
|
62
|
75
|
104
|
1) Distance d’arrêt.
Au voisinage d’un collège, un véhicule roule à 30 km/h, vitesse
maximale autorisée ; donner la valeur de la distance de réaction Dr,
de
la distance de freinage Df et calculer la valeur de la
distance d’arrêt
Da. Commenter la valeur de la distance d’arrêt obtenue en la
comparant
à celle d’une autre longueur ou distance que vous choisirez.
Dr = 8 m ; Df = 6 m ; Da = 8+6 = 14 m,
comparable à la longueur d'une grande salle de classe, à la hauteur
d'un arbre.
2) Energie
cinétique.
Rappeler l’expression de l’énergie cinétique d’un objet en fonction de
sa masse m et de sa vitesse V. Calculer l’énergie cinétique d’un
véhicule de masse m = 1000 kg roulant à 50 km/h. Lors du freinage,
l’énergie cinétique du véhicule diminue jusqu’à s’annuler. Décrire ce
que devient cette énergie.
Ec = ½mv2 avec m en kg, v en m / s.
Ec = 0,5 x 1000 x 142=9,8 104 J = 98
kJ.
Cette énergie est convertie en chaleur au niveau des freins, au moment
du freinage.
Sur autoroute, des panneaux expliquent aux conducteurs comment
respecter la distance de sécurité.
L’automobiliste doit veiller à ce que le véhicule qui le précède soit
séparé de lui d’au moins deux traits blancs sur le côté droit de la
route.
Le schéma ci-dessous représente les traits blancs et donne leurs
longueurs exprimées en mètres.
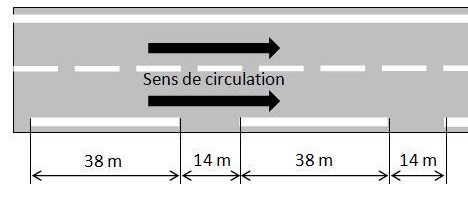
Sur autoroute et par temps sec, la vitesse des véhicules est limitée à
130 km/h.
Question : à l’aide
de calculs simples, expliquer pourquoi, sur autoroute, la règle « un
automobiliste doit veiller à ce que le véhicule qui le précède soit
séparé de lui d’au moins deux traits blancs » permet d’avoir une
distance de sécurité suffisante.
La distance de sécurité est égale à la distance parcourue par le
véhicule en 2 s, soit 72 m à la vitesse de130 km/h.
Distance correspondant à 2 traits blancs : 38+14+38=90 m.
Technologie.
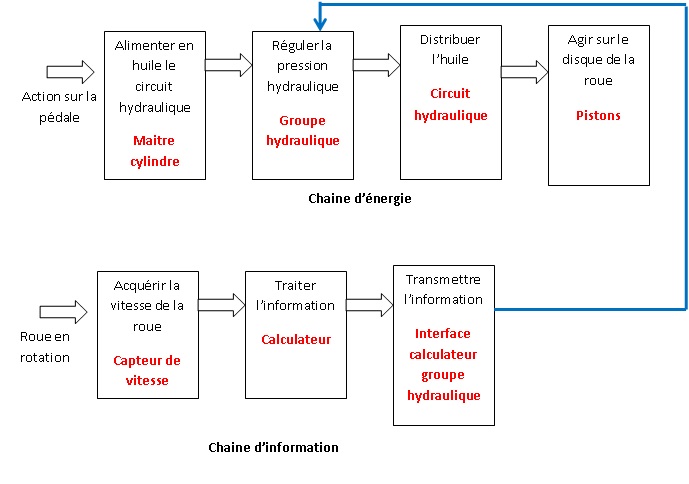
Le principe du freinage ABS est le suivant :
Lorsque le chauffeur appuie sur la pédale de frein, le maître-cylindre
alimente en huile le groupe hydraulique qui régule la pression d’huile
dans le circuit hydraulique. Les pistons portés par les étriers et
disposés de part et d’autre du disque sont poussés par l’huile sous
pression, ils pincent fortement le disque solidaire de la roue qui
ralentit. Si le pincement est trop fort, la roue peut se bloquer. Pour
éviter cela, un capteur détecte la vitesse de la roue et délivre cette
information au calculateur. Si la vitesse devient trop faible et proche
du blocage, le calculateur donne l’ordre au groupe hydraulique de
diminuer la pression. Ainsi, grâce à l’ensemble capteur de
vitesse-calculateur-groupe hydraulique, la pression est régulée lors
d’un appui sur la pédale de frein pour obtenir la meilleure efficacité
du freinage sans blocage.
1) Expliquer
pourquoi il est indispensable de doter les quatre roues d’un capteur de
vitesse.
Le blocage d'une seule roue peut entraîner la perte de contrôle du
véhicule.
Afin d'éviter qu'une roue ne se bloque, chaque roue doit être équiper
d'un capteur de vitesse.
2) Compléter la
figure en associant un composant matériel à chaque fonctionnalité.
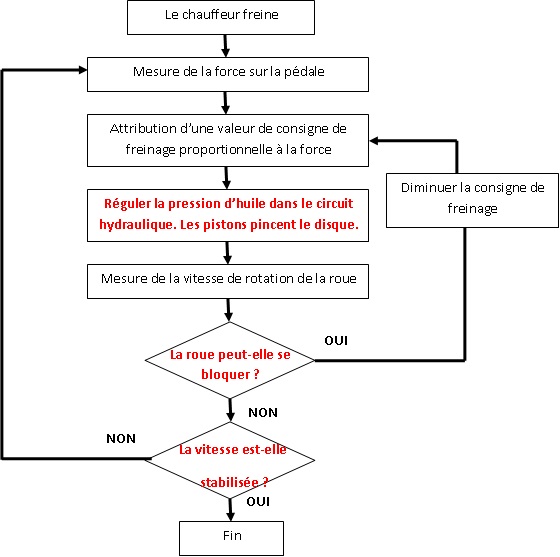
3) La figure
ci-dessous, présente l’algorithme du freinage ABS pour une roue.
Compléter les parties manquantes.
|
|
SVT.
Le comportement de l’automobiliste lors du freinage
Après avoir compris les distances d’arrêt et de sécurité d’un véhicule,
on s’intéresse maintenant au comportement de l’automobiliste lors du
freinage, en comparant celui-ci sans ou avec consommation d’alcool.
1) La durée de
réaction du conducteur, entre le moment où il voit l’obstacle et le
moment où il freine, correspond au temps de prise de décision et de
transmission des informations motrices jusqu’aux muscles des membres
inférieurs qui appuient sur la pédale de frein.
Question : à l’aide
de ces informations, compléter le schéma fonctionnel ci-dessous de la
commande volontaire du freinage chez un automobiliste.
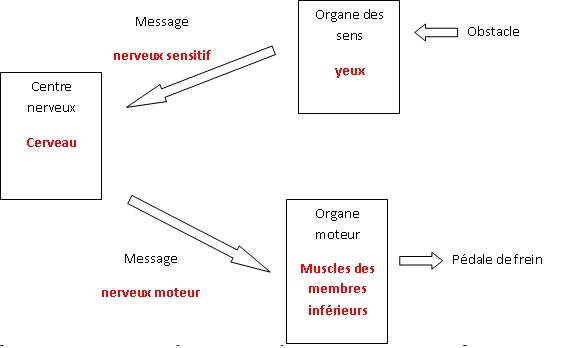
2) Lors d’une
expérimentation, on mesure la distance de réaction et la distance de
freinage d’une voiture lancée à 50 km/h, conduite par un individu à
jeun ou par un individu alcoolisé.
Les résultats de ces mesures sont donnés dans le tableau suivant :
Alcoolémie
( g /L) de sang
|
Distance
parcourue ( m)
|
Distance
de réaction DR
|
Distance
de freinage DF
|
0
|
14
|
16
|
0,5
|
22
|
16
|
0,8
|
26
|
16
|
Question :
déduire de ces résultats l’effet de l’alcool sur le freinage.
L'alcool augmente le temps de réaction donc la distance de réaction.
Une plus grande distance sera nécessaire pour arréter le véhicule. Par
contre la distance de freinage n'est pas modifiée.
3) Pour identifier
le mode d’action de l’alcool sur l’organisme du conducteur, on étudie
son effet sur des neurones du circuit de la motricité volontaire chez
un animal modèle, dont la sensibilité à l’alcool est identique à celle
de l’espèce humaine, selon le protocole schématisé dans le document 2a.
Les enregistrements ont été obtenus dans des situations d’alcoolisation
différentes (document 2b).
Questions :
préciser sur le document 2a le sens de circulation de l’information
nerveuse ;
Expliquer l’effet de l’alcool sur le comportement d’un conducteur lors
du freinage.
L'alcool a pour effet principal de ralentir l'activité du cerveau : un
retard de 2 ms est observé dans le cas d'alcoolisation.
|
|