Mathématiques, Brevet des collèges Pondichéry 2016 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Exercice 1.  Mélanie est une étudiante toulousaine qui vit en colocation dans un appartement. Ses parents habitent à Albi et elle retourne chez eux les week-ends. Elle rentre à Toulouse le dimanche soir. Sur sa route, elle passe prendre ses 2 colocataires à la sortie n° 3, dernière sortie avant le péage. Elle suit la route indiquée par l’application GPS de son téléphone portable, dont l’affichage est reproduit ci-après. 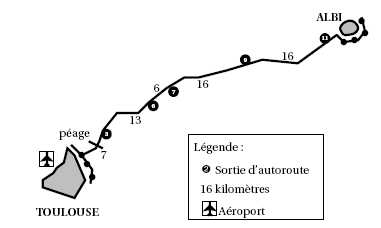Elle est partie à 16 h 20 et entre sur l’autoroute au niveau de la sortie n° 11 à 16 h 33. Le rendez-vous est à 17 h. Sachant qu’il lui faut 3 minutes pour aller de la sortie n° 3 au lieu de rendez-vous, à quelle vitesse moyenne doit-elle rouler sur l’autoroute pour arriver à l’heure exacte ? Vous donnerez votre réponse en km/h. Distance parcourue entre la sortie n°11 et la sortie n°3 : L=16+16+6+13 =51 km Durée du parcours : Dt = 16 h 57-16 h 33 min = 24 minutes ou 24 / 60 = 0,40 heure. Vitesse moyenne v = L / Dt = 51 /0,40 ~127,5 km /h. . . Exercice 2.  Le tableau ci-dessous fournit le nombre d’exploitations agricoles en France, en fonction de leur surface pour les années 2000 et 2010. A B C D 1 Surface de l'exploitation Nombre d'exploitations agricoles ( en milliers 2 En 2000 En 2010 3 Inférieure à 20 ha 359 235 4 Comprises entre 20 et 50 ha 138 88 5 Comprises entre 50 et 100 ha 122 98 6 Comprises entre 100 et 200 ha 64 73 7 Supérieure à 200 ha 15 21 8 Total 1. Quelles sont les catégories d’exploitations qui ont vu leur nombre augmenter entre 2000 et 2010 Les exploitations de plus de 100 ha ont vu leur nombre augmenter entre 2000 et 2010. 2. Quelle formule doit-on saisir dans la cellule B8 pour obtenir le nombre total d’exploitations agricoles en 2000 ? = SOMME(B3 :B7). 3. Si on étire cette formule, quel résultat s’affiche dans la cellule C8 ? 235 +88 +98 +73 +21 =515. 4. Peut-on dire qu’entre 2000 et 2010 le nombre d’exploitations de plus de 200 ha a augmenté de 40%? Justifier. (21-15) / 15 x 100 = 40 %. L'affirmation est vraie. ... Exercice 3. Un confiseur lance la fabrication de bonbons au chocolat et de bonbons au caramel pour remplir 50 boîtes. Chaque boîte contient 10 bonbons au chocolat et 8 bonbons au caramel. 1. Combien doit-il fabriquer de bonbons de chaque sorte ? 50 x10 = 500 bonbons au chocolat et 50 x 8 = 400 bonbons au caramel. 2. Jules prend au hasard un bonbon dans une boite. Quelle est la probabilité qu’il obtienne un bonbon au chocolat ? Nombre de bonbons au chocolat / Nombe total de bonbon =10 / 18 = 0,555 ~0,56. 3. Jim ouvre une autre boîte et mange un bonbon. Gourmand, il en prend sans regarder un deuxième. Est-il plus probable qu’il prenne alors un bonbon au chocolat ou un bonbon au caramel ? Oui, car le nombre de bonbons au chocolat est toujours supérieur au nombre de bonbons au caramel quel que soit le premier bonbon choisi. 4. Lors de la fabrication, certaines étapes se passent mal et, au final, le confiseur a 473 bonbons au chocolat et 387 bonbons au caramel. a. Peut-il encore constituer des boîtes contenant 10 bonbons au chocolat et 8 bonbons au caramel en utilisant tous les bonbons ? Justifier votre réponse. Il peut faire 47 boîtes de bonbons contenant 10 bonbons au chocolat et 8 bonbons au caramel. Il lui restera 3 bonbons au chocolat et  387 - 8 x47 =11 bonbons au caramel. b.  e confiseur décide de changer la composition de ses boîtes. Son objectif est de faire le plus de boîtes identiques possibles en utilisant tous ses bonbons. Combien peut-il faire de boîtes ? Quelle est la composition de chaque boîte ? 473 = 11 x 43 ; 387 = 9 x 43 ; PGCD (473 ; 387) = 43. Il peut constituer 43 boîtes contenant 11 bonbons au chocolat et 9 bonbons au caramel. Exercice 4. L’inspecteurG. est enmission dans l’Himalaya.Un hélicoptère est chargé de le transporter en haut d’une montagne puis de l’amener vers son quartier général. Le pilote : « Alors, je vous emmène, inspecteur ? » L’inspecteur : «OK, allons-y ! Mais d’abord, puis-je voir le plan de vol ? » Le trajet ABCDEF modélise le plan de vol. Il est constitué de déplacements rectilignes. On a de plus les informations suivantes :  AF= 12,5 km ; AC = 7,5 km ; CF = 10 km ; AB = 6 km ; DG = 7 km et EF = 750 m. (DE) est parallèle à (CF).  ABCH et ABGF sont des rectangles. 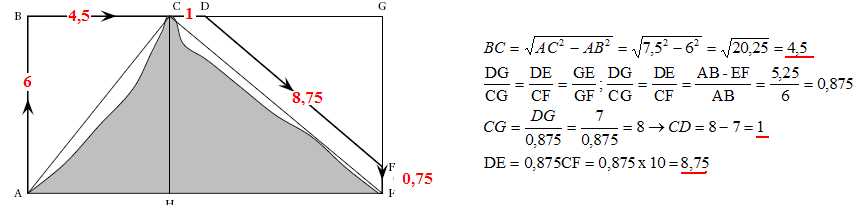Le pilote : « Je dois faire le plein . . . » L’inspecteur : « Combien consomme votre hélico ? » Le pilote : « 1,1 L par km pour ce genre de trajet » L’inspecteur : «Mais le plein nous surchargerait : 20 L de carburant seront très largement suffisants.  1. Vérifier que la longueur du parcours est de 21 kilomètres. 2. Le pilote doit-il avoir confiance en l’inspecteur G ? Justifier votre réponse. Consommation : 1,1 x 21 = 23,1 L. le pilote ne doit pas faire confiance à l'inspecteur. . . Exercice 5. Lors d’une course en moto-cross, après avoir franchi une rampe, Gaëtan a effectué un saut record en moto. Le saut commence dès que Gaëtan quitte la rampe. On note t la durée (en secondes) de ce saut. La hauteur (en mètres) est déterminée en fonction de la durée t par la fonction h suivante : h : t →(−5t −1,35)(t −3,7). Voici la courbe représentative de cette fonction h. 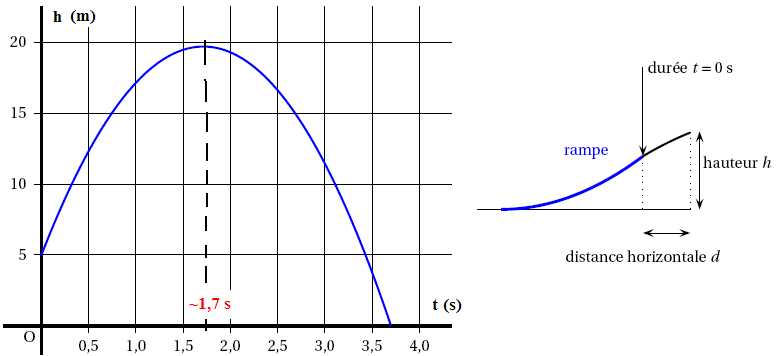Les affirmations suivantes sont-elles vraies ou fausses ? Justifier en utilisant soit le graphique soit des calculs. 1. En développant et en réduisant l’expression de h on obtient h(t ) = −5t2 −19,85t −4,995. Faux. -5t2+5 x 3,7 t-1,35 t+1,35x 3,7 = -5t2+17,15 t+4,995. 2. Lorsqu’il quitte la rampe, Gaëtan est à 3,8 m de hauteur. Faux. A t=0, h vaut déja 5 m ( lecture graphe ) et Gaêtan est qitte la rampe. 3. Le saut de Gaëtan dure moins de 4 secondes. Vrai. Sur le graphe on lit h = 0 pour t ~3,6 s. 4. Le nombre 3,5 est un antécédent du nombre 3,77 par la fonction h. -5 x3,52 +17,15 x 3,5 +4,995 = 3,77. Vrai. 5. Gaetan a obtenu la hauteur maximale avant 1,5 seconde. Faux. Sur le graphe,la hauteur maximale est atteinte  pour t ~1,7 s. Exercice 6. Lors des soldes, Rami, qui accompagne sa mère et s’ennuie un peu, compare trois étiquettes pour passer le temps : Etiquette 1 : Valeur 120 € ; soldé  105 €. Etiquette 2 : 45 €  ;-30%. Etiquette 3 : Soldes 25€ ; -12,50 € . 1. Quel est le plus fort pourcentage de remise ? Etiquette 1. (120-105) / 120 x 100 =12,5 % ; remise 15 €. Etiquette 2 : -30% ; remise 45 x 0,30 = 13,5 €. Etiquette 3 :12,50 / 25 x100 = 50 %. 2. Est-ce que la plus forte remise en euros est la plus forte en pourcentage ?  Non, la plus forte remise en euros correspond à l'étiquette1, plus petit pourcentage de remise ( -12,5 %). Exercice 7. Dans ce questionnaire à choix multiples, pour chaque question, des réponses sont proposées et une seule est exacte. Pour chacune des questions, écrire le numéro de la question et la lettre de la bonne réponse. Aucune justification n’est attendue. 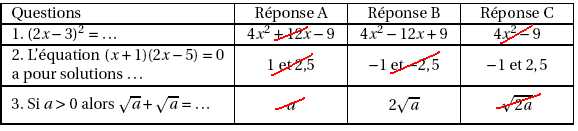Exercice 8. Afin de faciliter l’accès à sa piscine, Monsieur Joseph décide de construire un escalier constitué de deux prismes superposés dont les bases sont des triangles rectangles. 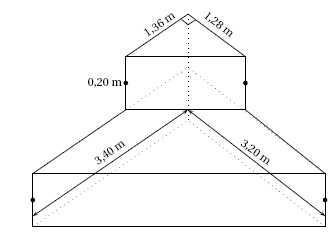1. Démontrer que le volume de l’escalier est égal à 1,262 08 m3. Aire de base du grand prisme : 3,40 x 3,20 / 2 =5,44 m2 ; hauteur 0,20 m.  Volume du grand prisme : aire de base fois hauteur = 5,44 x0,20 = 1,088 m3. Aire de base du petit prisme : 1,36 x 1,28 / 2 =0,8704 m2 ; hauteur 0,20 m.  Volume du petit prisme : aire de base fois hauteur = 0,8704 x0,20 = 0,17408 m3. Volume total : 1,088 +0,17408=1,262 08 m3. 2. Sachant que l’escalier est un ouvrage en béton courant, déterminer le nombre de sacs de ciment de 35 kg nécessaires à la réalisation de l’escalier. Un sac de ciment permet d'obtenir 100 L ( 0,100 m3) de béton.à partir de 5 seaux de sable, 8 seaux de gravillons et 17 L d'eau. Nombre de sacs de ciment : 1,26208 /0,100 = 12,62 soit 13 sacs de ciments. 3. Déterminer la quantité d’eau nécessaire à cet ouvrage. 12,62 x 17 = 214,5 L.

menu