Mathématiques, Brevet des collèges Nlle Calédonie 2015

Mathématiques, Brevet des collèges Nlle Calédonie 2015

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
Dans ce questionnaire à choix multiple, pour chaque question, une seule proposition est exacte. Pour chacune des questions, écrire le numéro de la question et recopier la bonne réponse. Aucune justification n’est attendue. Une réponse correcte rapporte 1 point. Une réponse fausse ou l’absence de réponse ne retire aucun point.
1. Marc a 10 ans et il pèse 30 kg. Quel sera son poids à 20 ans ?
On ne peut pas savoir ( proposition C).
2. Quelle est la largeur d’un rectangle de longueur 8 cm et de périmètre 24 cm ?
Périmètre = 2(longueur + largeur ) ; 12 = 8 + largeur ; largeur = 4 cm. ( proposition B).
3. Si je réponds à cette question au hasard, quelle est la probabilité que ma réponse
soit juste ?
Propositions : 1/3 ; 1/2 ; je ne peux pas savoir.
Une proposition juste sur les trois possibles, donc la probabilité est de 1/3.
4. Quel est le volume, arrondi à l’unité, d’une boule de rayon 3 cm?
4 / 3 p r³ = 4 / 3 x3,14 x3³ ~113 cm³. ( proposition A ).
5. Quelles sont les solutions de l’équation (x +1)(5x −10) = 0 ?
x+1=0 soit x = -1 ; 5x-10 = 0 soit x = 2. ( proposition C).

.
.

Exercice 2.
Un vendeur souhaite rendre son magasin plus accessible aux personnes en fauteuil roulant. Pour cela il s’est renseigné sur les normes et a décidé d’installer une rampe avec une pente de 3 degrés comme indiqué sur le schéma suivant.

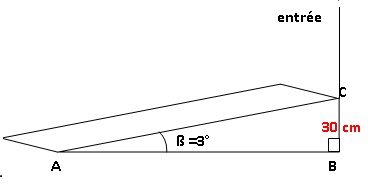
Calculer la longueur AB, arrondie au centimètre, pour savoir où la rampe doit commencer.
tan ß = BC / AB ; AB = BC / tan ß = 30 / tan 3 = 572 cm.

...

Exercice 3.
En 2010, l’UNESCO3 a dressé un inventaire des langues en danger dans le monde.
Il vise à susciter une prise de conscience sur la nécessité de préserver une diversité linguistique mondiale. Voici un tableau récapitulatif du nombre de langues en voie de disparition ou déjà éteintes :

Niveau de vitalité En voie de
disparition Déjà éteintes Total

Nombres de langues ...
231
2580

1. Sur 6 000 langues répertoriées, 43% sont soit en voie de disparition, soit déjà éteintes.
Montrer, par un calcul, que cela représente un total de 2 580 langues.
6000 x 0,43 = 2580.
2. En déduire le nombre de langues qui sont en voie de disparition.
2580-231=2349.
3. Calculer le pourcentage de langues qui sont déjà éteintes sur les 6 000 langues répertoriées dans le monde.
231 / 6000 x100 =3,85 %.

Exercice 4.
Pour répondre à la demande d’un client, un décorateur a besoin de découper des
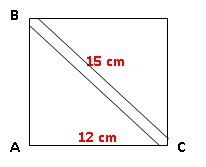
triangles dans du carrelage. Les triangles doivent être rectangles et isocèles avec une hypoténuse de longueur 15 cm. Les carreaux qu’il doit utiliser sont des carrés de 12 cm de côté.
Ces carreaux sont-ils assez grands pour faire deux de ces triangles dans chacun d’eux ?
Justifier.
Diagonale du carré de 12 cm de côté : BC²= 12² +12² = 288 cm² ; BC = 16,97 ~ 17 cm.
Oui c'est possible.

.
.

Exercice 5.
Une boîte «Chocodor »contient exactement 10 chocolats au lait, 8 chocolats noirs et 6 chocolats blancs.
Tous les chocolats ont la même forme et sont indiscernables au toucher.
1. Si l’on prend un chocolat au hasard dans cette boîte, quelle est la probabilité que ce soit un chocolat au lait ?
10 cas favorables sur 24 possibilités : probabilité : 10 / 24 = 5 / 12.
2. Alexis a acheté une boîte « Chocodor » et a déjà pris un chocolat de chaque sorte. Par gourmandise, il veut en prendre un quatrième sans regarder. Quelle est la probabilité que ce soit un chocolat noir ?
7 cas favorables sur 21 possibilités : probabilité : 7 / 21 = 1 /3.
3. Thomas a aussi acheté une boîte identique. Il l’a ouverte et a pris deux chocolats au hasard.
Quelle est la probabilité qu’il prenne deux chocolats blancs ?
Première prise : 6 cas favorables sur 24, probabilité : 6 /24 = 1 / 4.
Second tirage : 5 cas favorables sur 23, probabilité : 5 / 23.
1 /4 x 5 / 23 = 5 / 92.

Exercice 6.
On considère les polygones réguliers suivants :

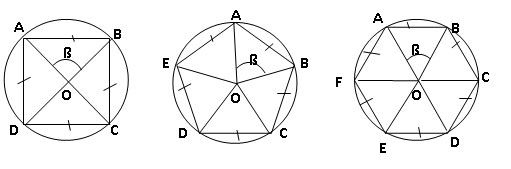
a. Le carré : Expliquer pourquoi l’angle� ß mesure 90°.
(AC) est la médiatrice de [BD].
b. Le pentagone régulier :
Expliquer pourquoi l’angle� ß mesure 72°.
Tous les triangles isocèles sont identiques : les cinq angles au centre ont la même mesure 360 / 5 = 72°.
c. L’hexagone régulier :
Calculer la mesure de l’angle ß.
Tous les triangles isocèles sont identiques : les six angles au centre ont la même mesure 360 / 6 = 60°.
2. Un polygone régulier a des côtés de longueur 5 cm. Les angles à chaque sommet mesurent 140°.
Calculer le périmètre de ce polygone.
Angle au centre dans un des triangles : 180 -140 = 40 °.
Nombre de côtés du polygone régulier: 360 / 40 = 9.
Périmètre du polygone régulier : 9 x5 = 45 cm.

Exercice 7.
Un collège a besoin de commander quelques livres de mathématiques et de français.
Chaque livre de mathématiques coûte 3 000 F et chaque livre de français 2 000 F.
Au total 30 livres ont été commandés pour un montant de 80 000 F.
Combien de livres de chaque sorte ont été commandés ?
x livres de mathématiques et y livres de français.
x+ y = 30 ; 3000 x + 2000 y = 80 000.
3000x +3000y =90 000 ; 3000 x + 2000 y = 80 000.
Soustraire : 1000 y = 10 000 ; y = 10 et x = 20.

Exercice 8.
Un site internet propose de télécharger légalement des clips vidéos. Pour cela, sur la page d’accueil, trois choix s’offrent à nous :
• Premier choix : téléchargement direct sans inscription. Avec ce mode, chaque clip peut être téléchargé pour 4 euros.
• Deuxième choix : téléchargement membre. Ce mode nécessite une inscription à 10 euros. valable un mois et permet d’acheter par la suite chaque clip pour 2 euros.
• Troisième choix : téléchargement premium. Une inscription à 50 euros permettant de télécharger tous les clips gratuitement pendant un mois.
1. Je viens pour la première fois sur ce site et je souhaite télécharger un seul clip. Quel est le choix le moins cher ?
Le premier choix revient à 4 €.
2. Pour cette question,
a. Compléter le tableau.

Nombre de clips
1
2
3
4
5

Prix pour le téléchargement direct
4
8
12
16
20

Prix pour le téléchargement membre
12
14
16
18
20

Prix pour le téléchargement premium 50
50
50
50
50

b. À partir de combien de clips devient-il intéressant de s’inscrire en tant que membre ?
A partir de 6 clips téléchargés, il vaut mieux être membre.
3. Dans cette question, x désigne le nombre de clips vidéos achetés.
f , g et h sont trois fonctions définies par :
• f (x) = 50
• g (x) = 4x
• h(x) = 2x +10
a. Associer chacune de ces fonctions au choix qu’elle représente (direct, membre ou premium).
f(x) : premium ; g(x) : direct ; h(x): membre.
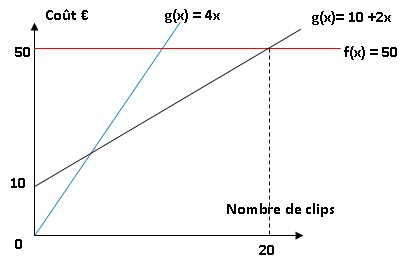
b. Tracer les droites représentant les fonctions f , g et h.
c. À l’aide du graphique, déterminer le nombre de clips à partir duquel l’offre premium devient la moins chère.
L'offre premium est la plus adaptée au delà de 21 clips.

Exercice 9.
Un marionnettiste doit faire un spectacle sur le thème de l’ombre. Pour cela il a besoin que sa marionnette de 30 cm ait une ombre de 1,2 m.
La source de lumière C est située à 8 m de la toile (AB).
La marionnette est représentée par le segment [DE].

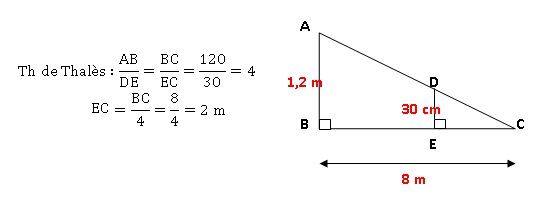
1. Démontrer que les droites (AB) et (DE) sont parallèles.
(AB) et (DE) sont toutes deux perpendiculaires à (BC).
2. Calculer EC pour savoir où il doit placer sa marionnette.

menu