Mathématiques,
Brevet des collèges Polynésie septembre 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
1. Voici un
programme de calcul :
Programme A.
• Choisir un nombre.
• Ajouter 3.
• Calculer le carré du résultat obtenu.
• Soustraire le carré du nombre de départ.
a. Eugénie choisit
4 comme nombre de départ. Vérifier qu’elle obtient 33 comme résultat du
programme.
(4+3)2-42=49-16=33.
b. Elle choisit
ensuite −5 comme nombre de départ. Quel résultat obtient-elle ?
(-5+3)2-(-5)2=4-25=
-21.
2. Voici un deuxième
programme de calcul :
Programme B.
• Choisir un nombre.
• Multiplier par 6.
• Ajouter 9 au résultat obtenu.
Clément affirme : « Si on choisit n’importe quel nombre et qu’on lui
applique les deux programmes, on obtient le même résultat. »Prouver que
Clément a raison.
Programme A : (n+3)2-n2=(n+3-n)(n+3+n)
= 3 (2n+3)= 6 n+9.
Programme B : 6 n+9
3. Quel nombre de départ faut-il
choisir pour que le résultat des programmes soit 54 ?
6n+9=54 ; n =
(54-9) / 6 = 45 /6=7,5.
Exercice 2.
Dans chaque cas,
dire si l’affirmation est vraie ou fausse (on rappelle que toutes les
réponses doivent être justifiées).
Affirmation 1
: l’angle ß mesure au dixième de degré près 36,9°. Vrai.
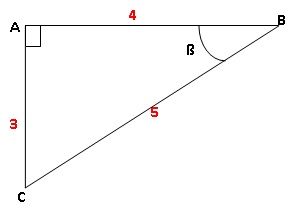
tan ß = AC / AB = 3 / 4 = 0,75 ; ß ~36,9°.
Affirmation
2. Le nombre 3 est une solution de l’équation x2 +2x
−15 = 0. Vrai.
32 +2 x3 -15 = 9+6-15=0.
Affirmation
3. Le prix avant la remise est de 63,70 €.
Faux.
Soldes −30%. Nouveau prix 49 €.
Remise : 63,7 x0,3 =19,11 €.
Nouveau prix : 63,70 -19,11 = 44,59 €.
Affirmation 4
: On a plus de chance de gagner en choisissant l’urne 2. Vrai.
Règle du jeu : Deux urnes contiennent des boules indiscernables au
toucher. On choisit une des
deux urnes et on en extrait une boule au hasard. On gagne si la boule
obtenue est rouge.
Urne 1 : 35 boules rouges et 65 boules blanches
Urne 2 : 19 boules rouges et 31 boules blanches.
Urne 1 : probabilité d'obtenir une boule rouge : 35 / (35+65) = 0,35.
Urne 2 : probabilité
d'obtenir une boule rouge :19 / (19+31) = 0,38.
|
| ... |
|
|
Exercice 3.
1.
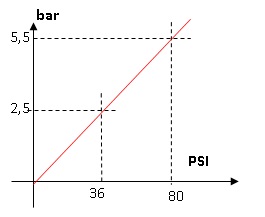
Le bar et le P.S.I. (Pound per Square Inch ou livre par pouce carré)
sont deux unités utilisées pour mesurer la pression. Le graphique
ci-dessous donne la correspondance entre ces 2 unités.
Avant de prendre la route, Léa vérifie la
pression des pneus de sa voiture. La
pression conseillée sur le manuel du véhicule est de 36 P.S.I.
Déterminer à l’aide du graphique la pression conseillée en bar.
2. Léa se rend à
Brest en prenant la route N 12 qui passe par Morlaix. Alors qu’elle se
trouve à 123 km de Brest, elle voit l'indication suivante : Brest 123
km ; Morlaix : 64 km.
Dans combien de kilomètres la distance qui la sépare de Morlaix sera la
même que celle de Morlaix à Brest ?
Distance Brest Morlaix : 123-64 = 59 km. 64-59 = 5 km.
Exercice 4.
Chez le fleuriste
un bouquet composé de 5 tulipes et 2 roses coûte 13,70 euros.
Une tulipe et une rose valent ensemble 4,30 euros.
Calculer le prix d’une tulipe et le prix d’une rose.
x : prix d'une
tulipe ; y : prix d'une rose.
5x +2y = 13,70
x+y = 4,30 soit 2x+2y = 8,60.
Soustraire : 3x = 13,70-8,60 =5,10 ; x = 5,10 / 3 = 1,70.
Par suite y = 4,30 -1,70 = 2,60.
|
|
|
|
Exercice 5.
Laurent s’installe comme éleveur de chèvres pour produire du lait afin
de fabriquer des fromages.
PARTIE 1 : La production de lait
Chèvre de race alpine :
Production de lait : 1,8 litre de lait par jour et par chèvre en
moyenne.
Pâturage : 12 chèvres maximum par hectare.
Plan simplifié des surfaces de pâturage.
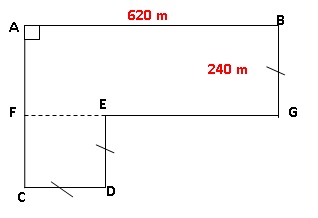
1. Prouver que
Laurent peut posséder au maximum 247 chèvres.
Aire du rectangle ABGF : 620 x240 =148 800 m2= 14,88 ha.
Aire du carré CDEF : 240 x240 = 57600 m2= 5 76 ha.
Aire totale : 14,88 + 5,76 = 20,64 ha.
Nombre maximal de chèvres : 20,64 x12 ~247 .
2. Dans ces
conditions, combien de litres de lait peut-il espérer produire par jour
en moyenne ?
247 x1,8 = 444,6 L.
Le stockage du lait
Laurent veut acheter une cuve cylindrique pour stocker le lait de ses
chèvres.
Il a le choix entre 2 modèles :
• cuve A : contenance 585 litres
• cuve B : diamètre 100 cm, hauteur 76 cm
Il choisit la cuve ayant la plus grande contenance. Laquelle va-t-il
acheter ?
Volume de la cuve B : pr2h
= 3,14 x502x76 =596 903 cm3 = 596,9 L. Il chosit
la cuve B.
Exercice 6.
Germaine souhaite réaliser un escalier pour monter à l’étage de son
appartement.
Elle a besoin pour cela de connaître les dimensions du limon (planche
dans laquelle viendront se fixer les marches de cet escalier).
Elle réalise le croquis ci-dessous.
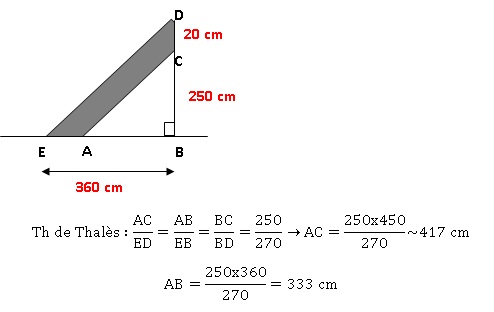
le limon est représenté par le quadrilatère ACDE.
les droites (AC) et (ED) sont parallèles.
les points E, A et B sont alignés.
les points B, C et D sont alignés.
1. Prouver que ED =
450 cm.
ED2 = EB2 +BD2 = 3602 +2702=202
500 ; ED = 450 cm.
2. Calculer les
deux dimensions AC et AE de cette planche. Arrondir les résultats au
centimètre.
AE = 360-333 = 27 cm.
|
|
Exercice 7.
La
distance d’arrêt est la distance que parcourt un véhicule entre le
moment où son conducteur voit un obstacle et lemoment où le véhicule
s’arrête.
Une formule permettant de calculer la distance d’arrêt est :
D =5 / 18 ×V +0,006×V 2 où D : est la distance d’arrêt en m
; V : la vitesse en km/h
1. Un conducteur
roule à 130 km/h sur l’autoroute. Surgit un obstacle à 100 m de lui.
Pourra-t-il s’arrêter à temps ?
D = 5 / 18 x 130 +0,006 x1302=36,11 +101,4 = 137,5 m. Non,
il ne s'arrête pas à temps.
On a utilisé un tableur pour calculer la distance d’arrêt pour quelques
vitesses.
Une copie de l’écran obtenu est donnée ci-dessous. La colonne B est
configurée pour afficher les résultats arrondis à l’unité.
|
A
|
B
|
1
|
Vitesse
( km /h)
|
Distance
d'arrêt (m)
|
2
|
30
|
14
|
3
|
40
|
21
|
4
|
50
|
29
|
5
|
60
|
38
|
6
|
70
|
49
|
7
|
80
|
61
|
8
|
90
|
74
|
Quelle formule a-t-on saisie dans la cellule B2 avant de la recopier
vers le bas ?
=5 / 18 *A2+0,006*A2*A2
3. On entend
fréquemment l’affirmation suivante : « Lorsqu’on va deux fois plus
vite, il faut une distance deux fois plus grande pour s’arrêter ».
Est-elle exacte ?
Faux. A 30 km /h, la distance d'arrêt est 14 m ; à 60 km/h, la distance
d'arrêt est 38 m.
4. Au code de la
route, on donne la règle suivante pour calculer de tête sa distance
d’arrêt : « Pour une vitesse comprise entre 50 km/h et 90 km/h,
multiplier
par lui-même le chiffre des dizaines de la vitesse ».
Le résultat calculé avec cette règle pour un automobiliste qui roule à
80 km/h est-il cohérent avec celui calculé par la formule ?
8 x8 = 64 m, valeur cohérente avec 61 m.
|
|