Mathématiques,
Brevet des collèges Polynésie 2014
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
On
place des boules toutes indiscernables au toucher dans un sac. Sur
chaque boule colorée est inscrite une lettre. Le tableau suivant
présente la répartition des boules :
|
rouge
|
vert
|
bleu
|
A
|
3
|
5
|
2
|
B
|
2
|
2
|
6
|
1. Combien y a-t-il
de boules dans le sac ?
3 +5 +2 +2 +2 +6 = 20.
2. On tire une
boule au hasard, on note sa couleur et sa lettre.
a. Vérifier qu’il y
a une chance sur dix de tirer une boule bleue portant la lettre A.
Nombre de cas favorables ( boule bleu marquée A) = 2.
Nombre de boules = 20 ;
Probabilité de tirer une boule bleue : 2 / 20 = 0,10.
b. Quelle est la
probabilité de tirer une boule rouge ?
5 boules rouges ; probabilité de tirer une boule rouge : 5 /20 = 0,25.
c. A-t-on autant de
chance de tirer une boule portant la lettre A que de tirer une boule
portant la lettre B?
Oui, 10 boules sont marquées A et 10 boules sont marquées B.
Exercice 2.
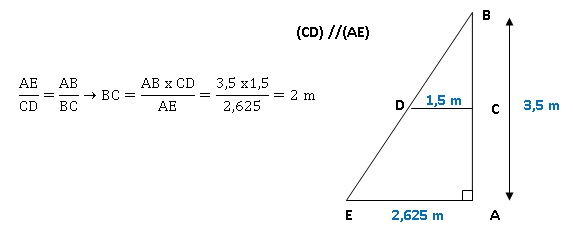
Pour
construire un mur vertical, il faut parfois utiliser un coffrage et un
étayage qui maintiendra la structure verticale le temps que le béton
sèche. Cet étayage peut se représenter par le schéma suivant.
1. Calculer BE.
BE2 = AE2 +AB2 =2,6252 +3,52
=19,14 ; BE =4,375 m.
2. Les barres [CD] et [AE] doivent être parallèles.
À quelle distance de B faut-il placer le point C?
|
|
|
Exercice 3.
La copie d’écran ci-dessous montre le travail
effectué par Léa pour étudier trois fonctions f , g et h telles que :
• f (x) = x2+3x −7
• g (x) = 4x +5
• h est une fonction affine dont Léa a oublié d’écrire l’expression
dans la cellule A4.
S=
|
=B1*B1+3B1-7
|
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
x
|
-2
|
0
|
2
|
4
|
6
|
2
|
f(x)=x2+3x-7
|
-9
|
-7
|
3
|
21
|
47
|
3
|
g(x)=4x+5
|
-3
|
5
|
13
|
21
|
29
|
4
|
h(x)
|
9
|
5
|
1
|
-3
|
-7
|
1.
Donner un nombre qui a pour image −7 par la fonction f .
L'image de 0 par la fonction f est égale à -7..
2. Vérifier à
l’aide d’un calcul détaillé que f (6) = 47.
62+3 x6-7 = 36+18-7=47
3. Expliquer
pourquoi le tableau permet de donner une solution de l’équation :
x2+3x −7 = 4x +5. Quelle est cette solution ?
Dans la partie grisée du tableau rechercher la valeur identique
figurant dans une colonne.
L'antécédent de 21 est 4, solution de l'équation.
4. À l’aide du
tableau, retrouver l’expression algébrique h(x) de la fonction affine h.
h(x) = ax +b avec a et b des constantes.
h(0) = b = 5 ; h(2) =2 a+5=1 d'où a
= -2 ; h(x) = -2x+5.
Exercice 4.
Deux affirmations
sont données ci-dessous. Pour chacune des affirmations, indiquer
si elle est vraie ou fausse. On rappelle que toutes les réponses
doivent être justifiées.
Affirmation 1
: Les diviseurs communs à 12 et 18 sont les mêmes que les diviseurs de
6.
12 et 18 sont des multiples de 6. Le PGCD de 12 et 18 est égal à 6.
L'affirmation est vraie.
Affirmation 2
: les nombres suivants sont entiers. Vrai.
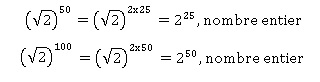
|
|
|
|
Exercice 5.
Les appareils de la maison consomment de l’énergie
même quand
ils sont en veille. La feuille de calcul ci-dessous donne la
consommation en kilowattheures (kwh) des appareils en veille d’une
famille pour une année et les dépenses correspondantes en euros :
|
A
|
B
|
C
|
D
|
E
|
1
|
Appareil
|
Nombre
|
Consommation
en veille
par an par appareil ( kWh)
|
Prixn
du kWh ( €)
|
Dépense
( €)
|
2
|
téléviseur
|
3
|
77
|
0,13
|
30,03
|
3
|
ordinateur
|
1
|
209
|
0,13
|
21,17
|
4
|
parabole
|
2
|
131
|
0,13
|
34,06
|
5
|
four
|
1
|
86
|
0;13
|
11,18
|
6
|
démodulateur
|
3
|
59
|
0,13
|
23,01
|
7
|
lecteur
DVD
|
2
|
58
|
0,13
|
15,08
|
8
|
machine
à laver
|
1
|
51
|
0,13
|
6,63
|
9
|
console
de jjeu
|
1
|
42
|
0,13
|
5,46
|
10
|
micro-ondes
|
1
|
25
|
0,13
|
3,25
|
11
|
téléphone
sans fil
|
1
|
25
|
0,13
|
3,25
|
12
|
lave-vaisselle
|
1
|
17
|
0,13
|
2,21
|
13
|
chargeur
batterie
|
4
|
13
|
0,13
|
6,76
|
14
|
|
|
|
Dépense totale
|
168,09
|
1. a. Quel calcul
permet de vérifier le résultat 34,06 affiché dans la cellule E4 ?
2 x131 x0,13 = 34,06 €
b. Quelle formule
a-t-on saisie dans la cellule E2 avant de la recopier vers le bas ?
=B2*C2*0,13
c. Une des quatre
formules ci-dessous a été saisie dans la cellule E14 pour obtenir le
montant total des dépenses dues aux veilles. Recopier sur la
copie cette formule.
= SOMME(E2 : E13)
; = E2 : E13 ; = E2+E13 ; = SOMME(E2 : E14)
2. Dans une pièce
de cette maison, les appareils qui sont en veille sont :
• un téléviseur • une console de jeu • un ordinateur • un lecteur DVD
La consommation de l’ordinateur représente-t-elle plus de la moitié de
la consommation totale des appareils de cette pièce ?
Consommation totale : 77 +42 +209 +58 = 386 kWh.
386 / 2 = 193 kWh.
Consommation ordinateur : 209 kWh, valeur supérieure à 193.
L'ordinateur consomme plus de la moitié de la consommation des
appareils en veille.
Exercice 6.
Une
famille de quatre personnes hésite entre deux modèles de piscine. Elle
regroupe des informations afin de prendre sa décision.
Piscine ronde de diamètre 3,4 m, de hauteur intérieure 1,20 m.
Piscine octogonale de diamètre extérieur 4,40 m, hauteur intérieure
1,20 m,
La construction d’une piscine de surface au sol de moins de 10 m2
ne nécessite aucune démarche administrative.
Surface minimale conseillée par baigneur : 3,40 m2.
Aire d’un octogone régulier : 2x11,414×R2 où R est le
rayon du disque extérieur à l’octogone.
Débit du robinet de remplissage : 12 litres d’eau par minute.
1. Chacun des
modèles proposés impose-t-il des démarches administratives ?
Aire de la piscine ronde pR2
= 3,14 x1,72 =9,08 m2, pas d'autorisation.
Aire de la piscine octogonale : 2x1,414x2,22 = 13,7 m2,
une autorisation est nécessaire.
2. Les quatre
membres de la famille veulent se baigner en même temps. Expliquer
pourquoi la famille doit dans ce cas choisir la piscine octogonale.
Surface minimale pour 4 baigneurs : 4 x3,4 = 13,6 m2. Seule
la piscine octogonale convient.
3. On commence le
remplissage de cette piscine octogonale le vendredi à 14 h 00 et on
laisse couler l’eau pendant la nuit, jusqu’au samedi matin à 10 h 00.
La piscine va-t-elle déborder ?
Débit du robinet : 12 L d'eau par minute.
Volume de la piscine : aire de base x hauteur = 13,7 x1,2 = 16,4 m3.
Durée d'ouverture du robinet : 20 heures soit 20 x60 = 1200 minutes.
Volume d'eau écoulée : 12 x1200 = 14 400 l = 14,4 m3, valeur
inférieur au volume de la piscine.
La piscine ne déborde pas.
|
|
Exercice 7.
Dans
tout cet exercice, on travaille avec des triangles ABC isocèles en A
tels que : BC = 5 cm. La mesure de l’angle� ABC peut varier.
On va alors s’intéresser aux angles extérieurs de ces triangles,
c’est-à-dire, comme l’indique la figure ci-après, aux angles qui sont
supplémentaires et adjacents avec les angles de ce triangle.
1. Dans cette
question uniquement, on suppose que� l'angle ABC = 40 °.
a. Construire le triangle ABC en vraie grandeur.
Aucune justification n’est attendue pour cette construction.
b. Calculer la
mesure de chacun de ses 3 angles extérieurs.
c. Vérifier que la
somme des mesures de ces 3 angles extérieurs est égale à 360 °.
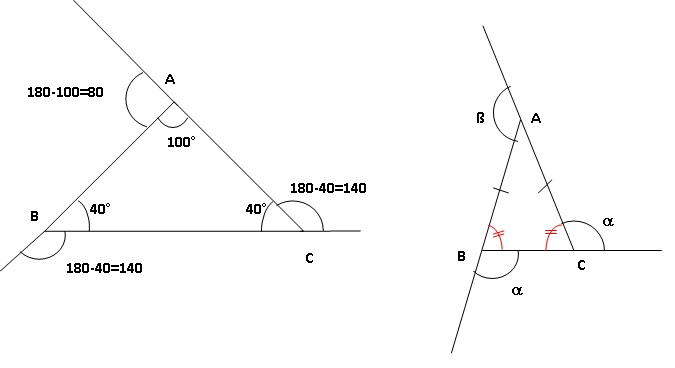
Somme des angles extérieurs : 80 +140+140 = 360°.
2. Est-il possible
de construire un triangle ABC isocèle en A tel que la somme des mesures
de ses trois angles extérieurs soit différente de 360 ° ?
Somme des angles extérieurs : 2 a
+ ß
Somme des angles du triangle isocèle en A : 180-ß +2 (180-a) = 180.
-ß -2a +360 =0 ;
2 a + ß = 360.
La construction est impossible.
|
|