Math�matiques, Brevet des coll�ges Centres �trangers 2014

Math�matiques, Brevet des coll�ges Centres �trangers 2014

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

Exercice 1.
Voici une feuille de calcul obtenue � l’aide d’un tableur.
Dans cet exercice, on cherche � comprendre comment cette feuille a �t� remplie.

A
B
C

1
216
126
90

2
126
90
36

3
90
36
54

4
54
36
18

5
36
18
18

1. En observant les valeurs du tableau, proposer une formule � entrer dans la
cellule C1, puis � recopier vers le bas.
=A1-B1
2. Le tableur fournit deux fonctions MAX et MIN. � partir de deux nombres,
MAX renvoie la valeur la plus grande et MIN la plus petite. (exemple MAX(23 ; 12) = 23)
Quelle formule a �t� entr�e dans la cellule A2, puis recopi�e vers le bas ?
=MIN(A1 ; B1)
3. Que repr�sente le nombre figurant dans la cellule C5, par rapport aux nombres 216 et 126 ?
216 = 2³ x3³ ; 126= 2 x3²x7 ; PGCD(216 ; 126) = 2 x3² =18.
4. La fraction 216 /126 est-elle irr�ductible ? Si ce n’est pas le cas, la rendre irr�ductible
en d�taillant les calculs.

.
.

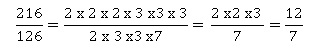
Exercice 2.
� Pise vers 1200 apr�s J. C. (probl�me attribu� � L�onard de Pise, dit Fibonacci, math�maticien
italien du moyen �ge). Une lance, longue de 20 pieds, est pos�e verticalement le long d’une tour consid�r�e comme perpendiculaire au sol. Si on �loigne l’extr�mit� de la lance qui repose sur le sol de 12 pieds de la tour, de combien descend l’autre extr�mit� de la lance le long du mur ?
* Un pied est une unit� de mesure anglo-saxonne valant environ 30 cm.

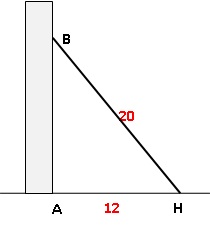
AB² = BH²-AH² =20²-12²=400-144=256 ; AB = 16 pieds
La lance descend de 20-16 = 4 pieds le long du mur.

Exercice 3.
Attention les figures trac�es ne respectent ni les mesures de longueur, ni les mesures d’angle
R�pondre par � vrai � ou � faux � ou � on ne peut pas savoir � � chacune des affirmations
suivantes et expliquer votre choix.
1. Tout triangle inscrit dans un cercle est rectangle. Faux.
Un triangle ABC inscrit dans un demi-cercle de diam�tre AB est rectangle en C.
2. Si un point M appartient � la m�diatrice d’un segment [AB] alors le triangle AMB est isoc�le.
Vrai.
Un point de la m�diatrice est �quidistant des extr�mit�s du segment.
3 et 4.

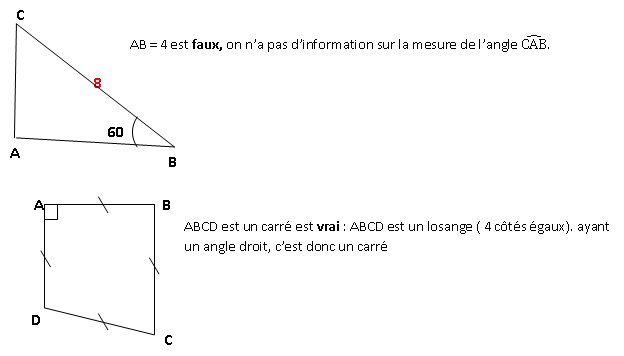
Exercice 4.
Paul en visite � Paris admire la Pyramide, r�alis�e en verre feuillet� au centre de la cour int�rieure du Louvre. Cette pyramide r�guli�re a :
• pour base un carr� ABCD de c�t� 35 m�tres ;
• pour hauteur le segment [SO] de longueur 22 m�tres.
Paul a tellement appr�ci� cette pyramide qu’il ach�te comme souvenir de sa visite une lampe � huile dont le r�servoir en verre est une r�duction � l’�chelle 1 /500 de la vraie pyramide.
Le mode d’emploi de la lampe pr�cise que, une fois allum�e, elle br�le 4 cm³ d’huile par heure.
Au bout de combien de temps ne restera-t-il plus d’huile dans le r�servoir ? Arrondir � l’unit� d’heures.
Rappel : Volume d’une pyramide = un tiers du produit de l’aire de la base par la hauteur
Dimensions du r�servoir d'huile : base carr�e de c�t� 35 /500 =0,07 m = 7 cm et de hauteur 22/500 = 0,044 m = 4,4 cm.
Volume de ce r�servoir : aire de base x hauteeur / 3 = 7 x7 x4,4 / 3 = 71,87 cm³.
Dur�e = 71,87 / 4 ~ 18 heures.

.
.

Exercice 5.
1. D�velopper et r�duire l’expression : (2n+5)(2n−5) o� n est un nombre quelconque.
(2n+5)(2n-5)=4n²+10n -10n -25 = 4n²-25.
2. En utilisant la question 1, calculer 205�195.
205 x195 = 200²-25 = 39975.

Exercice 6.
Pour pr�parer son voyage � Marseille, Julien utilise un site Internet pour choisir le meilleur itin�raire. Voici le r�sultat de sa recherche :
Calculez votre itin�raire 59 000 Lille–13000 Marseille
Co�t estim� P�age 73,90 €
Carburant 89,44 €
Temps 8 h 47 dont 8 h 31 sur autoroute
Distance 1004 km dont 993 km sur autoroute.
1. Quelle vitesse moyenne, arrondie au km/h, cet itin�raire pr�voit-il pour la portion de trajet sur autoroute ?
8 h 31 = 8 x60 +31 = 511 min ; vitesse = 993 / 511 =1,943 km / min soit 1,943 x60 = 116,6 ~117 km /h.
2. Sachant que la s�curit� routi�re pr�conise au moins une pause de 10 � 20 minutes toutes les deux heures de conduite, quelle doit �tre la dur�e minimale que Julien doit pr�voir pour son voyage ?
8 h 47 min + 4 x10 min = 8 h + 87 min = 9 h 27 min.
3. Sachant que le r�servoir de sa voiture a une capacit� de 60 L et qu’un litre d’essence co�te 1,42 €, peut-il faire le trajet avec un seul plein d’essence en se fiant aux donn�es du site internet ?
Volumr de carburant : 89,44 / 1,42 ~63 L, valeur sup�rieure au volume du r�servoir.

Exercice 7.
Il existe diff�rentes unit�s demesure de la temp�rature : en France on utilise le degr� Celsius (�C), aux Etats-Unis on utilise le degr� Fahrenheit (� F).
Pour passer des degr�s Celsius aux degr�s Fahrenheit, on multiplie le nombre de d�part par 1,8 et on ajoute 32 au r�sultat.
1. Qu’indiquerait un thermom�tre en degr�s Fahrenheit si on le plonge dans une casserole d’eau qui g�le ? On rappelle que l’eau g�le � 0 �C
0 x1,8 +32 = 32 �F.
2. Qu’indiquerait un thermom�tre en degr�s Celsius si on le plonge dans une casserole d’eau port�e � 212 �F ? Que se passe t-il ?
(212-32) / 1,8=100�C.
L'eau bout � 100 �C sous une pression de 1 bar.
3. a. Si l’on note x la temp�rature en degr� Celsius et f (x) la temp�rature en degr� Fahrenheit, exprimer f (x) en fonction de x.
f(x) = 1,8 x +32.
b. Comment nomme-t-on ce type de fonction ?
Fonction affine.
c. Quelle est l’image de 5 par la fonction f ?
f(5) = 1,8 x5 +32 = 41.
d. Quel est l’ant�c�dent de 5 par la fonction f ?
5 = 1,8 x +32 ; 1,8 x = 5-32 ; 1,8 x = -27 ; x = -27 /1,8 =-15.
e. Traduire en terme de conversion de temp�rature la relation f (10) = 50.
10 �C correspond � 50 �F.

menu