Mathématiques, Brevet des collèges Nlle Calédonie 03 /2014

Mathématiques, Brevet des collèges Nlle Calédonie 03/2014

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Exercice 1. QCM
1. Sur cette figure, les points K, F, R et K,M, P sont alignés.
KF = 3, KR = 9, KM= 4, KP = 12. Les droites (FM) et (RP) sont-elles parallèles ?

Réponse A.
2. Si on remplace x par −3 dans l’expression 5−2x, on trouve :
5-2x(-3) = 11. Réponse B.
3 On a représenté la fonction f dans le repère ci-dessous :

L’image de 2 par la fonction f est 1. Réponse A.
4. En utilisant le même graphique que la question 3.
2 a trois antécédents par la fonction f . Réponse C.
f(0,4 )=f( 1,2)=f( 4) = 2.

.
.

Exercice 2.
C’est en 1891 que les premiers vietnamiens arrivèrent en Nouvelle-Calédonie pour travailler dans les mines de nickel. De nos jours, leurs descendants continuent à transmettre leur héritage au travers de manifestations culturelles. Un des symboles de cet héritage est celui du «Nón lá » communément appelé chapeau chinois. On considère que ce chapeau est un cône.

1. Calculer la hauteur SO, arrondir à l’unité.
SO²= SM² -OM² = 37,5² -24² =830,25 ; SO = 28,81 ~29 cm.
2. En guise de décoration, on se propose de poser un ruban rouge autour du chapeau
parallèlement à sa base.
Ce ruban est disposé au tiers du chapeau en partant du sommet.
a. Quelle est la nature de la figure géométrique formée par ce ruban?
Un cercle de centre C et de rayon CN= 8 cm.
b. Calculer en cm la longueur du ruban.
2pR = 2 x3,14 x8 ~ 50,3 cm

...

Exercice 3.
Chaque année les professeurs de mathématiques de la Nouvelle-Calédonie organisent
le Rallye maths des collégiens. Pour l’année 2013, l’équipe organisatrice est confrontée à un problème de répartition des cadeaux des trois premières classes figurant au classement final.
1. Avec 292 crayons, 219 règles et 73 calculatrices. Combien de lots identiques peut-on constituer pour en avoir le plus possible et en utilisant tout le stock ? Justifier la réponse.
219 = 3 x73 ; 292 = 4 x73.
PGCD ( 292 ; 219 ; 73) =73.
On peut réaliser 73 lots identiques.
2. Quelle serait alors la composition de chacun des lots ? Justifier la réponse.
292 / 73 = 4 crayons ; 219 / 73 = 3 règles ; 73 / 73 = 1 calculatrice.
3. On suppose que le nombre de lots est de 73 lots. Sachant que l’effectif total de ces trois classes est de 80 élèves, quelle est la probabilité qu’un élève choisi au hasard ne reçoive aucun lot ?
7 cas favorables sur 80 possibilités : 7 / 80 =0,0875.

Exercice 4.
• On donne 6 nombres répartis dans six bulles.
• Vous devez trouver des étapes de calcul permettant d’obtenir le résultat affiché au centre.
• Vous pouvez utiliser les 4 opérations autant de fois que vous le voulez.
• Vous ne pouvez pas utiliser deux fois le même nombre (ou la même expression).
• Vous n’êtes pas obligé d’utiliser tous les nombres (ou les expressions) affichés.
Prenons pour exemple la liste des nombres donnée ci-dessous, en utilisant les 4 opérations,
on doit trouver 155 :

On peut, par exemple, proposer les étapes de calcul suivant :
• 50×3 = 150
• 10÷2 = 5
• 150+5 = 155 (qui est la solution à trouver ).
1. Avec les données de l’exemple précédent, proposer des étapes de calcul pour obtenir 367.
50 x8 = 400 ; 400 -25 = 375 ; 375-10 = 365 ; 365+2 = 367.
2. On donne maintenant la série de nombres suivante.

Proposer des étapes de calcul permettant d’obtenir 15 / 6.
1 / 2 x 5 / 3 = 5 / 6 ; 5 / 6 x3 = 15 / 6.
À partir des expressions réparties dans les six bulles ci-dessous, proposer des étapes de calcul permettant d’obtenir 4x²+6x −1.

5x²-x² = 4x² ; 4x² +8x-2x = 4x² +6x ; 4x² +6x +1.

Exercice 5.
Voici les résultats du DNB blanc de deux classes de 3e d’un collège de Nouméa.
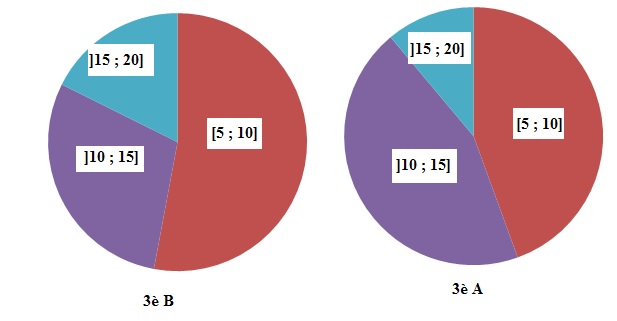
Pour la 3e A, on a : 8 ; 7 ; 12 ; 15 ; 15 ; 12 ; 18 ; 18 ; 11 ; 7 ; 8 ; 11 ; 7 ; 13 ; 10 ; 10 ; 6 et 11.
Pour la 3e B, on a : 7 ; 8 ; 7 ; 9 ; 8 ; 13 ; 8 ; 13 ; 13 ; 8 ; 19 ; 13 ; 7 ; 16 ; 18 ; 12 et 9.
1. Calculer la moyenne de chaque classe, arrondie au dixième. Que constate-t on ?
(8 +7 +12 +15 +15 +12 +18 +18 +11 +7 +13 +10 +10 +6 +11) / 18=11,1.
(7+8+7 +9 +8 +13 +8 +13 +13 +8 +19 +13 +7 +16 +18 +12 +9) / 17 =11,1.
La moyenne est la même.
2. Calculer ensuite leurs médianes.
Classer les notes par ordre croissant :
6 ;7 ; 7 ; 7 ; 8 ; 8 ; 10 ; 10 ; 11 ; 11 ; 11 ; 12 ; 12 ; 13 ; 15 ; 15 ; 18 ; 18 : médiane : 11.
7 ; 7 ;7 ; 8 ; 8 ; 8 ; 8 ; 9 ; 9 ; 12 ; 13 ; 13 ; 13 ; 13 ; 16 ; 18 ; 19 : médiane : 9.
3. Quelle est, d’après les calculs, la classe ayant le mieux assimilé les leçons ? Justifier la réponse.
Pour la 3è A, la moitié des élève sont un note supérieure ou égale à 11, alors que pour l'autre classe, la moitié des élèves ont une note inférieure ou égale à 9.
4. Deux des graphiques donnés ci-dessous représentent la répartition des notes des classes précédentes.
Attribuer à chaque classe le graphique qui lui correspond..

Exercice 6.
L’origami est le nomjaponais de l’art du pliage du papier. A partir d’un carré de 15 cm, on donne ci-dessous le début du canevas de pli de la grue japonaise.

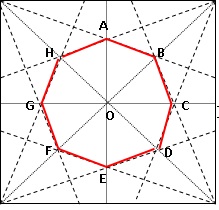
1. Cette construction fait apparaitre un polygone régulier ABCDEFGH de centre O. Est-ce un pentagone, un octogone ou un hexagone ?
huit côtés, donc octogone.
2. Calculer alors la mes ure de l’angle AOB.
360 / 8=45°.
3. Calculer ensuite la mesure de l’angle OAB.
Le triangle OAB est isocèle en O.
(180-45) / 2 = 67,5°.
4. On donne OA = OC = 4,5 cm. Calculer la longueur AC. Arrondir au dixième.
Le triangle OAC est rectangle en O.
AC² = OA² +OC² = 4,5² +4,5² = 40,5 ; AC ~6,4 cm.

Exercice 7.
Au marché municipal de Nouméa, on trouve toutes sortes de légumes et de fines herbes.
• la botte de persil vaut 20 F de plus que la botte d’oignons verts ;
• la botte de basilic coûte le même prix que la botte de menthe ;
• la botte de menthe coûte cinq fois moins cher que le kilogramme de salade verte ;
• le kilogramme de salade verte est à 900 F, soit six fois le prix d’une botte d’oignons verts.
Chacune des affirmations suivantes est-elle vraie ou fausse ? Les réponses doivent être justifiées.
Affirmation 1 : avec 700 F, on peut acheter 6 bottes d’oignons verts. Faux.
Prix des oignons verts : 900 /6= 150 F.
Le persil vaut : 150+20 =170 F.
La menthe ou du basilic vaut : 900 / 5=180 F.
6 bottes d'oignons verts valent 150 x6 = 900 F.
Affirmation 2 : avec 700 F, on peut acheter une botte de menthe, une botte d’oignons verts, une botte de basilic et une botte de persil. Vrai.
180 + 150 + 180 + 170=680 F.
Affirmation 3 : avec 1 500 F, on peut acheter 2 bottes de chacune des fines herbes (la salade ne fait pas partie des fines herbes). Vrai.
2(150 + 170 +180 +180) =1360 F.

Exercice 8.
Une feuille de calcul d’un tableur est représentée ci-dessous. Pour chaque question, une seule des trois réponses proposées est exacte. Sur la copie, indiquer le numéro
de la question et recopier, sans justifier, la proposition choisie. Aucun point ne sera enlevé en cas demauvaise réponse.

A
B
C
D

1
35
21
18

2

3
=A1*B1+C1
35 x 21+18=753 ( réponse C)
=MAX(A1 ; C1)
35 ( réponse A)
=SOMME(A1 : C1)
35+21+18=74 ( réponse B)

4

5

.

menu