Mathématiques,
Brevet des collèges Polynésie 09 / 2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice 1.
Le
diagramme en bâtons ci-dessous nous renseigne sur le nombre de buts
marqués lors de la seconde édition de la coupe de l’Outre-Mer de
football en 2010.
Nombre de buts marqués par ligue
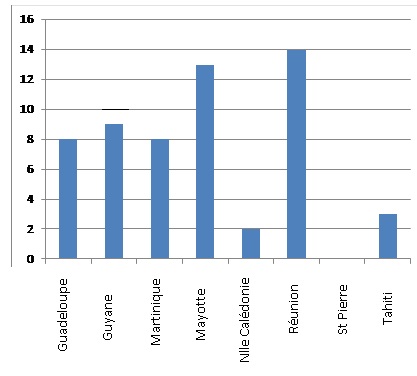
1. Combien de buts
a marqué l’équipe de Mayotte ? 13.
2. Quelle est
l’équipe qui amarqué le plus de buts ? Réunion.
3. Quelle(s)
équipe(s) ont marqué strictement moins de 8 buts ?
Nlle Calédonie ; St Pierre ; Tahiti.
4. Quelle(s)
équipe(s) ont marqué au moins 10 buts ?
Mayotte ; Réunion.
5. Quel est le
nombre total de buts marqués lors de cette coupe de l’Outre-Mer 2010 ?
8+9+8+13+2+14+0+3=57.
6. Calculer la
moyenne de buts marqués lors de cette coupe de l’Outre-Mer 2010.
Nombre de matchs ( chaque ligue rencontre toutes les autres) : 8 x7 / 2
= 28.
57 / 28 ~ 2 buts par match..
7. Compléter les
cellules B2 à B10 dans le tableau ci-dessous.
|
A
|
B
|
1
|
Ligues
d'Outre Mer
|
Nombre
de buts marqués
|
2
|
Gadeloupe
|
8
|
3
|
Guyane
|
9
|
4
|
Martinique
|
8
|
5
|
Mayotte
|
13
|
6
|
Nlle
Calédonie
|
2
|
7
|
Réunion
|
14
|
8
|
St
Pierre
|
0
|
9
|
Tahiti
|
3
|
10
|
Total
|
57
|
11
|
Moyenne
|
environ
2
|
8. Parmi
les propositions suivantes, entourer la formule que l’on doit écrire
dans la cellule B10 du tableau pour retrouver le résultat du nombre
total de buts marqués.
8+9+8+13+2+14+0+3 ; = TOTAL(B2 :B9) ; =SOMME(B2
:B9).
9. Écrire dans la
cellule B11 du tableau précédent une formule donnant la moyenne des
buts marqués.
=B10/28 ; moyenne par matcchs ; =B10/8 ( moyenne par ligue)
Exercice
2.
Heiata
et Hiro ont choisi comme gâteau de mariage une pièce montée composée de
3 gâteaux cylindriques superposés, tous centrés sur l’axe (d).
Les trois gâteaux
cylindriques sont de même hauteur : 10 cm.
• Le plus grand gâteau cylindrique, le n° 1, a pour rayon 30 cm.
• Le rayon du gâteau n° 2 est égal au 2 /3 de celui du gâteau n° 1.
• Le rayon du gâteau n° 3 est égal au 3 /4 de celui du gâteau n° 2.
1. Montrer que le
rayon du gâteau n° 2 est de 20 cm.
30 x2 / 3=20 cm.
2. Calculer le
rayon du gâteau n° 3.
20 x3 / 4 = 15 cm.
3. Montrer que le
volume total exact de la pièce montée est égal à 15 250p cm3.
Volume du cylindre n°1 : p
R12h =302 x10 p =9000 p cm3.
Volume du cylindre n°2 : p R22h
=202 x10 p
=4000 p
cm3.
Volume du cylindre n°3 : p R32h
=152 x10 p
=2250 p
cm3.
Volume total : 5 250p cm3.
4. Quelle fraction du volume total
représente le volume du gâteau n° 2 ? Donner le résultat sous forme de
fraction irréductible.
4000 / 15250 = 400 / 1525 = 16 / 61.
|
| ... |
|
|
Exercice 3.
La 24e édition du Marathon International de Moorea a
eu lieu le 18 février 2012.
Des coureurs de différentes origines ont participé à ce marathon :
• 90 coureurs provenaient de Polynésie Française dont 16 étaient des
femmes
• 7 coureurs provenaient de France Métropolitaine dont aucune femme,
• 6 provenaient d’Autriche dont 3 femmes,
• 2 provenaient du Japon dont aucune femme,
• 11 provenaient d’Italie dont 3 femmes,
• 2 provenaient des Etats-Unis dont aucune femme
• Un coureur homme était Allemand.
1. Compléter le
tableau ci-dessous à l’aide des données de l’énoncé.
|
Polynésie
|
Métropole
|
Autriche
|
Japon
|
Italie
|
USA
|
Germany
|
Femme
|
16
|
0
|
3
|
0
|
3
|
0
|
0
|
2. Combien de
coureurs ont participé à ce marathon ?
90 +7 +6 +2 +11 +2 +1 = 119.
3. Parmi les
participants à ce marathon, quel pourcentage les femmes polynésiennes
représentent-elles ? Arrondir au dixième près.
16 / 119 x100 = 13,4 %.
À la fin du marathon, on interroge un coureur au hasard.
4. Quelle est la
probabilité que ce coureur soit une femme Autrichienne ?
3 / 119 =0,0252.
5. Quelle est la
probabilité que ce coureur soit une femme ?
22 / 119 = 0,1849.
6. Quelle est la
probabilité que ce coureur soit un homme Polynésien?
74 / 119 = 0,6218.
7. Quelle est la
probabilité que ce coureur ne soit pas Japonais ?
117 / 119 =0,9832.
8. Vaitea dit que
la probabilité d’interroger un coureur homme Polynésien est exactement
trois fois plus grande que celle d’interroger un coureur homme non
Polynésien.
A-t-il raison ? Expliquer pourquoi.
P(homme polynésien) = 0,6218.
Nombre d'hommes : 119-22 =97 ; nombre d'hommes non polynésien = 97-74
=23
P( homme non polynésien) = 23 / 119 =0,1933.
0,1933 x3 =0,579, différent de 0,6218. Il a tord.
Exercice 4.
Voici le parcours du cross du collège La Bounty schématisé par la
figure ci-dessous :
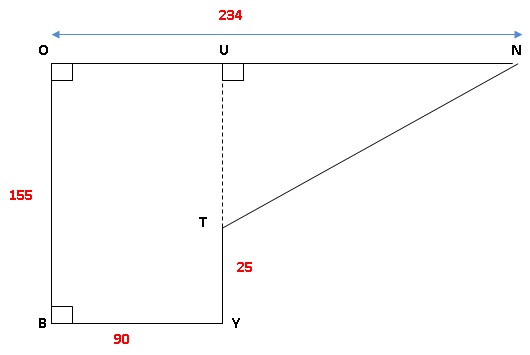
1. Montrer que la
longueur NT est égale à 194 m.
UT = 155 -25 = 130 m ; UN = 234-90 = 144 m ;
NT2 = UT2 +UN2=1302 +1442
= 37636 ; NT = 194 m.
2. Le départ et
l’arrivée de chaque course du cross se trouvent au point B.
Calculer la longueur d’un tour de parcours.
155 +234 +194 +25 +90 = 698 m.
3. Les élèves de 3e
doivent effectuer 4 tours de parcours.
Calculer la longueur totale de leur course.
4 x 698 = 2792 m.
4.
Terii, le vainqueur de la course des garçons de 3ème a effectué sa
course en 10 minutes et 42 secondes. Calculer sa vitesse moyenne et
l’exprimer en m /s. Arrondir au centième près.
10 min 42 s = 10 x60 +42 = 642 s.
vitesse ( m/s) = distance (m) / durée (s) =2792 / 642 = 4,35 m /s.
5.
Si Terii maintenait sa vitesse moyenne, penses-tu qu’il pourrait battre
le champion Georges Richmond qui a gagné dernièrement la course sur 15
km des Foulées du Front de mer en 55 minutes et 11 secondes ?
55 min 11 s = 55 x60 +11 = 3311 s.
Distance parcourue à la vitesse moyenne de 4,35 m /s :
4,35 x3311 ~14,4 km, valeur inférieure à 15 km. La réponse est non.
.
|
|
|
|
Exercice 5.
Teiki
se promène en montagne et aimerait connaître la hauteur d’un Pinus (ou
Pin des Caraibes) situé devant lui. Pour cela, il utilise un bâton et
prend quelques mesures au sol. Il procède de la façon suivante :
Il pique le bâton en terre, verticalement, à 12 mètres du Pinus.
- La partie visible (hors du sol) du bâton mesure 2 m.
- Teiki se place derrière le bâton, de façon à ce que son oeil, situé à
1,60 m au dessus du sol, voie en alignement le sommet de l’arbre et
l’extrémité du bâton.
- Teiki marque sa position au sol, puis mesure la distance entre sa
position et le bâton. Il trouve alors 1,2 m.
On peut représenter cette situation à l’aide du schéma ci-dessous :
1. Quelle est la hauteur du Pinus
au-dessus du sol ?
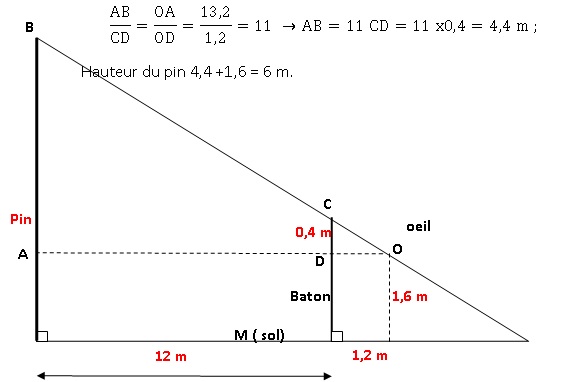
Exercice 6.
L’île d’Aratika est au Nord de l’île de Fakarava.
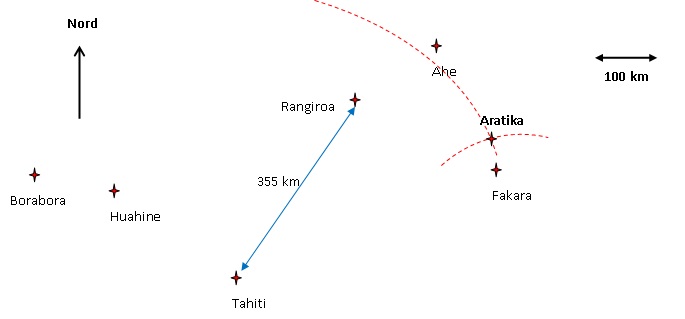
A l’aide des documents suivants et de l’Annexe 1 et en considérant que
tous les vols entre Tahiti et les îles des Tuamotu se font à la même
vitesse moyenne, placer avec le plus de précision possible l’île
d’Aratika sur l’Annexe 1 en expliquant en détail sur ta copie ta
démarche.
Document 1 : Temps de vol
entre Tahiti et les îles des Tuamotu (Nord) :
Tahiti–Rangiroa : 55 min Tahiti–Ahe : 1 h 15 min
Tahiti–Apataki : 1 h 05 min Tahiti–Aratika : 1 h 15 min
Tahiti–Arutua : 1 h 05 min.
Document 2 :
Distance entre les îles :
Tahiti–Moorea : 17 km Apataki–Arutua : 17 km Tahiti–Bora Bora : 268 km
Fakarava–Aratika : 50 km Tahiti–Raiatea : 210 km Fakarava–Faaite : 21 km
Tahiti–Rangiroa : 355 km Faaite–Anaa : 61 km Tahiti–Huahine : 175 km.
Vitesse moyenne de l'avion : 355 / 55 = 6,45 km / min.
Distance Tahiti- Aratika : 6,45 x (60+15) =484 km.
Echelle : 1,4 cm pour 100 km.
Tracer un cercle, centré sur Tahiti, de rayon 4,84 x1,4 ~6,8 cm.
Tracer un cercle, centré sur Fakarava, de rayon 50 x1,4 /100 ~0,7 cm.
|
|