Mathématiques, Brevet des collèges Centres étrangers 2012

Mathématiques, Brevet des collèges Centres étrangers 2012

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
1. Calculer :

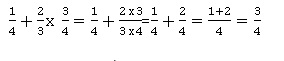
2. Au goûter, Lise mange 1 / 4 du paquet de gâteaux qu’elle vient d’ouvrir.
De retour du collège, sa soeur Agathe mange les 2 / 3 des gâteaux restants dans le paquet entamé par Lise. IL reste alors 5 gâteaux.
Quel était le nombre initial de gâteaux dans le paquet ?
On note a le nombre de gateau.
Lise en mange : a / 4 = 0,25 a ; il en reste 0,75 a.
Agathe mange : 0,75 a x 2 /3 = 0,5 a ; il en reste 0,25 a = 5 soit a = 20.

.
.

Exercice 2.
Une usine doit fabriquer des boîtes cylindriques de contenance 250 cm³de hauteur h et de rayon x.
1. On suppose que x = 3 cm.
a.Montrer que h ≈ 8,8 cm.
volume d’un cylindre : px² h ; 3,14 x3² xh = 250 ; h = 250 /(3,14 x9) = 8,84 cm.
b. La surface latérale du cylindre est une plaque rectangulaire de largeur 8,8 cm et de longueur L..
Calculer une valeur approchée de L au mm près.
L = 2 px = 2 x3,14 x3 = 18,849 ~18,8 cm.
2. On a représenté ci-dessous la hauteur de la boîte en fonction du rayon.

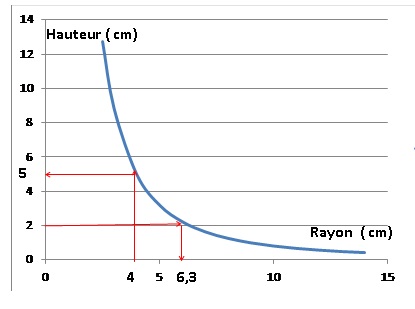
a. La fonction représentée est-elle une fonction affine ? Justifier.
Non, le graphe n'est pas une droite.
b. Par lecture graphique, indiquer :
• quel est approximativement le rayon correspondant à une hauteur de 2 cm. 6,3 cm.
• quelle est approximativement la hauteur correspondant à un rayon de 4 cm. 5 cm.

Exercice 3.
On considère les programmes de calcul suivants :
Programme A
• Choisir un nombre.
• Lui ajouter 1
• Calculer le carré de la somme obtenue
• Soustraire au résultat le carré du nombre de départ.
Programme B
• Choisir un nombre
• Ajoute 1 au double de ce nombre
1. On choisit 5 comme nombre de départ. Quel résultat obtient-on avec chacun des deux programmes ?
A : 5 +1 = 6 ; 6² = 36 ; 36-5² = 36-25 = 11.
B : 5 x2 +1 = 11.
2. Démontrer que quel que soit le nombre choisi, les résultats obtenus avec les deux programmes sont toujours égaux.
A : (n+1)² -n² = (n+1+n)(n+1-n) =2n+1.
B : 2n+1.

Exercice 4. QCM.

.
.

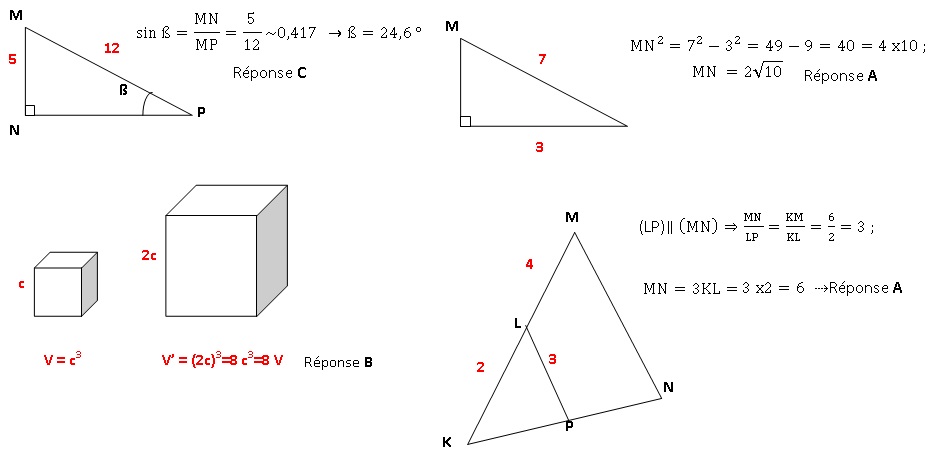
Exercice 5.
Lors de sa sortie au Mont Saint Michel, un élève achète un souvenir dans une boutique.
Cet objet est assimilé à un solide composé d’une calotte sphérique de rayon 4,5 cm posée sur un cylindre de hauteur 3,8 cm.
Voici ci-dessous une représentation en perspective de cet objet :

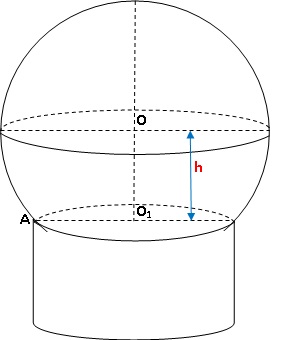
O est le centre de la calotte sphérique et O₁est le centre d’une des bases du cylindre.
A est un point de la section du cylindre avec la sphère de centre O et O₁A = 3,6 cm.
1. a. Montrer que la distance OO₁ = 2,7 cm.
OO₁² = OA²-AO₁² = 4,5² -3,6² = 7,29 ; OO₁ = 2,7 cm.
b. Quelle est la hauteur totale de l’objet ?
3,8 +2,7 +4,5 = 11 cm.
2. a. La maquette du Mont Saint Michel qui est à l’intérieur de la calotte sphérique est assimilée à un cône de hauteur 4,7 cm dont la base a pour rayon 3,6 cm.Montrer qu’une valeur approchée du volume de cette maquette est 64 cm³.
Volume d’un cône : 1/3 × aire de base × hauteur.
1 / 3 x3,14 x3,6² x4,7 =63,7 ~64 cm³.

Exercice 6.
Dans le cadre d’un projet pédagogique, des professeurs préparent une sortie au Mont SaintMichel avec les 48 élèves de 3e.
Deux activités sont au programme :
• la visite duMont et de son abbaye ;
• la traversée à pied de la baie duMont Saint Michel.
Partie 1 : Financement de la sortie
Le coût total de cette sortie (bus, hébergement et nourriture, activités, ... ) s’élève à 120 € par élève.
1. Le FSE (foyer socio-éducatif ) du collège propose de prendre en charge 15% du coût total de cette sortie.
Quelle est la somme prise en charge par le FSE ?
120 x48 x0,15 = 864 €.
2. Pour réduire encore le coût, les professeurs décident d’organiser une tombola.
Chaque élève dispose d’une carte contenant 20 cases qu’il doit vendre à 2 € la case.
En décembre, les professeurs font le point avec les 48 élèves sur le nombre de cases vendues par chacun d’entre eux.
Voici les résultats obtenus :

Nombre de cases vendues
10
12
14
15
16
18
20

Nombre d'élèves
5
12
9
7
5
6
4

a. Quel est le nombre total de cases déjà vendues en décembre ?
10 x5 +12 x12 +14 x9 +15 x7 +16 x5 +18 x6 +20 x4 =50 +144 +126 +105 +80 +108 +80 =693.
b. Quelle somme d’argent cela représente-t-il ?
693 x2 = 1386 €.
c. Quel est le pourcentage d’élèves ayant vendu 15 cases ou moins ? (arrondir à l’unité).
(5 +12 +9 +7) / 48 = 0,6875 ( ~69 %)
d. Quel est le nombre moyen de cases vendues par élève ? (arrondir à l’unité).
693 / 48 = 14,4 ~ 14.
3. Les 92 lots à gagner sont les suivants :
• un vélo ; • un lecteur DVD; • 20 DVD; • 20 clés USB de 4 GO; • 50 sachets de chocolats.
Ces lots sont fournis gratuitement par trois magasins qui ont accepté de sponsoriser le projet.
Le triage au sort a lieu aumois de mars. Les 960 cases ont toutes été vendues. Une personne a acheté une case.
a. Quelle est la probabilité que cette personne gagne un lot ? (arrondir au centième)
92 / 960 = 0,0958 ~0,096.
b. Quelle est la probabilité que cette personne gagne une clé USB? (arrondir au centième).
20 / 960 = 0,0208 ~0,021.

Exercice 7.
Avant la sortie, les professeurs de mathématiques donnent ces deux exercices à leurs élèves.
1. Alexandre souhaite savoir à quelle distance il se trouve du Mont à l’aide d’un théodolite (appareil servant à mesurer des angles). Il sait que le sommet S du Mont est à 170 m d’altitude. Son oeil (O sur le dessin) étant situé à 1,60 m du sol, il obtient la mesure suivante :� SOH= 25 °. (Le dessin n’est pas réalisé à l’échelle).
1. À quelle distance LK du Mont se trouve-t-il ? (Donner une valeur approchée au mètre).

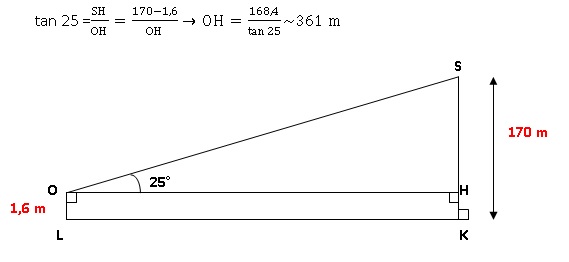
2. Sachant que le Mont est inscrit dans un rectangle de 225 m sur 285 m , on peut dire que la superficie de la partie émergée du Mont se situe :
• entre 10 000 m² et 40 000 m²,
• entre 40 000 m² et 80 000 m²,
• entre 80 000 m² et 150 000m²,
• entre 150 000 m² et 200 000 m².
Quelle est la bonne réponse ? Justifier.
225 x285 =64 125 m². Entre 40 000 m² et 80 000 m².

Le Mont Saint Michel est entouré par la mer qui est soumise au phénomène des marées.
La traversée de la baie ne peut se faire qu’à marée basse.
a. Quel jour la marée est-elle basse à 11 h 14 min ? Jeudi 3.
b. Le samedi 5, quelle est la durée écoulée entre les deux « pleines mers » ?
19 h13 - 6 h 58 = 12 h 15 min.
2. Les professeurs souhaitent faire la traversée un mardi après midi. Avant de fixer une date, ils regardent le calendrier des marées.
Quel mardi doivent-ils choisir ? Justifier. Mardi 8.
La basse mer a lieu à 15 h 09.
3. Le trajet prévu est long de 13 km et devra se faire en 2 h 30 min. Quelle sera la vitesse moyenne du groupe en km/h.
13 / 2,5 = 5,2 km / h.

menu