Un projet novateur
: Solar impulse 2,
bac
Sti2d Stl Nlle Calédonie 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
Partie A. Examen médical préparatoire du
pilote .
Pendant le trajet, les capacités physiques sont mises à rude épreuve.
Avant le départ, le pilote doit vérifier sa bonne résistance cardiaque.
C'est pourquoi une scintigraphie du myocarde peut lui être prescrite
par son médecin.
A.1 Donner deux raisons qui
justifieraient un tel examen ?
Le muscle cardiaque, soumis à rude épreuve durant le vol, doit
être parfaitement irrigué et se contracté correctement.
A.2 Le technétium
99 (Tc 99), émetteur ß- , est utilisé pour cet examen. C'est
le plus courant des isotopes de cet élément.
A.2.1 Définir le
terme isotope.
Deux isotopes ne diffèrent que par leur nombre de neutrons. Ils ont le
même numéro atomique.
A.2.2 Ecrire
l'équation de désintégration ß- du Tc 99. Identifier le
noyau fils.
9943Tc ---> AZX +0-1e.
Conservation de la charge : 43 = Z-1 ; Z = 44 ( élément ruthénium )
Conservation du nombre de nucléons : A+0 = 99.
9943Tc
---> 9944Ru
+0-1e.
A.3 Lors de la désintégration du Tc
99, un des rayonnements émis possède une énergie, E, égale à 294 keV.
A.3.1 Donner
l'expression littérale de la longueur d'onde, l., de ce rayonnement dans
le vide, en fonction de E et des constantes physiques.
l = hc
/ E.
A.3.2 Calculer la
valeur numérique de l.,
en picomètres (1 pm = 10-12 m).
294 keV = 2,94 105 eV = 2,94 105 x1,6 10-19
= 4,704 10-14 J
6,63 10-34 x3 108 / (4,704 10-14)~4,2
10-12 m = 4,2 pm.
A.3.3 Préciser à
quel domaine des ondes électromagnétiques appartient ce rayonnement. Rayons X.
A.4 La demi-vie
d'un échantillon radioactif est la durée au bout de laquelle la moitié
des noyaux initialement présents a été désintégrée.
A.4.1 Pourquoi la
demi-vie du technétium est-elle compatible avec un examen médical ?
Sa demi-vie est courte ( environ 6 heures). Il disparaît de l'organisme
par désintégration au bout d'environ 60 heures ( 4 jours).
A.4.2 Retrouver la
valeur de la demi-vie du technétium. Détailler le raisonnement.
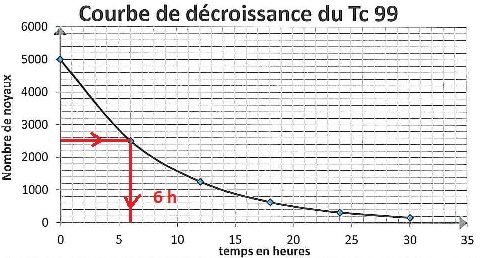
A.5 Lors de
l'examen médical le pilote de 75 kg reçoit une dose de 2, 5 mL de Tc 99
d'activité A0 = 62 MBq. Quelques minutes plus tard, les
premières images du coeur sont visualisées grâce à une gamma-caméra à
scintillations.
A.5.1 Définir
l'activité d'un échantillon.
L'activité, exprimée en Bq, est le nombre de désintégrations par
seconde.
A.5.2 Donner la
relation entre le nombre de noyaux radioactifs, N, d'un échantillon et
son activité, A.
A = l N avec l = ln 2 / T.
A.5.3 Montrer que
le nombre de noyaux radioactifs, N0 , reçus par le patient
lors de l'injection est de 1, 9. 1012.
Donnée: constante radioactive du technétium : l= 3, 21x10-5 s-1
.
N0 = 62 106 / (3,21 10-5) ~1,9 1012.
A.5.4 En déduire la
masse, m0 ,de technétium reçue par le pilote.
Masse d'un noyau de technétium 99 : m(Tc) = 1, 65 x 10-25 kg.
m0 = 1,9 1012 x1,65 10-25 ~3,2 10-13
kg.
A.5.5 Une partie du
rayonnement peut être absorbée par l'organisme humain. La « dose
d'énergie, D, absorbée » est:
D =E / m avec E en joule et m en kg.
Parmi les unités suivantes, quelle est celle de la dose d'énergie
absorbée, D ?
Curie Becquerel Gray Sievert
A.5.6 Calculer la
dose d'énergie, D, absorbée par le pilote, sachant que l'énergie reçue
lors de l'injection est de 1,0 10- 2 J.
D = 75 / (1,0 10-2) = 7,5 103 Gy.
A.5.7 Citer un
risque pour l'organisme humain lié à la radioactivité.
Cancer.
|
|
|
|
Partie
B. Echanges énergétiques soleil- cellules photovoltaïques et cellules -
batterie.
B.1 Bilan énergétique pour
les cellules photovoltaïques
B.1.1 Compléter la
chaîne énergétique .
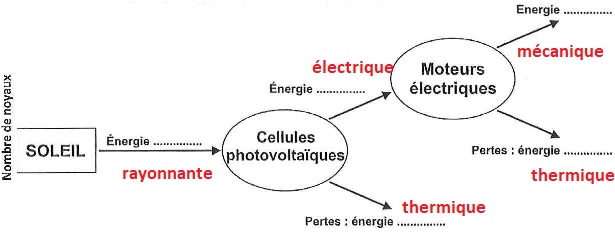
B.1.2 Calculer la
puissance solaire moyenne, PR, absorbée par l'ensemble des
cellules photovoltaïques, pendant que le Soleil brille.
Entre Le Caire et Abou Dhabi la puissance solaire moyenne en juillet
est de 380 W /m2 . Le soleil brille en moyenne 14 h par jour.
Surface des cellules 269,5 m2.
PR = 380 x269,5 ~ 1,0 105 W.
B.1.3 Montrer que
l'énergie solaire, ER, reçue par l'ensemble des cellules
photovoltaïques lors d'une journée de vol vaut 1, 43 x 106
W. h.
1,0 105 x 14 ~1,43 106 Wh.
B.1.4 Exprimer
l'énergie, Emot reçue par les moteurs, en fonction du
rendement, h= 22,7 %, des
cellules et de l'énergie, ER. Calculer sa valeur numérique
pour une journée.
Emot = ER h = 1,43 106
x0,227=3,25 105 Wh.
B.2 Bilan énergétique pour la propulsion
B.2.1 Calculer, en
watts, la puissance totale, Pmot pour l'ensemble des quatre
moteurs de Solar Impulse 2 .
4 moteurs électriques de puissance 17, 5 cv chacun. 1cv= 0,736 kW.
4 x17,5 x736 =5,15 104 W.
B.2.2 En déduire
l'énergie, E'mot nécessaire à leur fonctionnement pendant
une journée de 14 h.
5,15 104 x14 =7,21 105 Wh.
B.2.3 L'énergie, Emot
est-elle suffisante pour alimenter les quatre moteurs de l'avion ?
Justifier la réponse.
E'mot > Emot, les moteurs ne peuvent pas être
alimentés grâce à l'énergie électrique d'origine solaire, pendant 14
heures.
B.3 Rôle des batteries en
décharge
Les batteries utilisées sont entièrement chargées au départ. Elles se
déchargent, notamment la nuit, pour permettre à l'avion de voler en
l'absence de lumière et sont rechargées le jour lors des phases de
planage.
B.3.1 Avancer au
moins deux raisons qui justifient le choix de batteries
lithium-polymères pour Solar Impulse 2.
L'énergie stockée par kilogramme de batteries est plus élevée que celle
des autres batteries.
Durée de vie importante.
B.3.2 A l'aide des
demi-équations fournies, identifier l'oxydant qui réagit lors de la
décharge. Justifier la réponse.
Oxydation du lithium à l'anode négative : LiC6 --> Li+
+e- +6C.
Réduction de Li+ à la cathode positive : MnO2 +Li+
+e- ---> LiMnO2.
B.3.3 Déterminer
l'équation de la réaction ayant lieu lors de la décharge des batteries.
LiC6 + MnO2 --> LiMnO2
+6C.
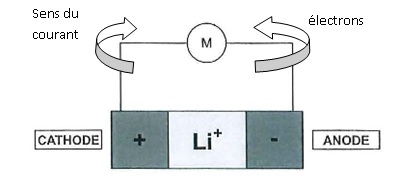
B.3.4 Compléter le document en
indiquant, en décharge, le sens de circulation des électrons et le sens
du courant.
B.3.5 Compléter la
chaîne énergétique des batteries en décharge.
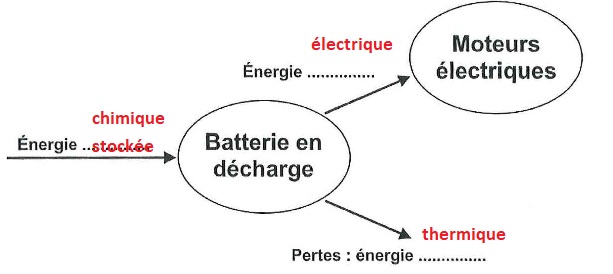
8.3.6 Calculer
l'énergie disponible, Ehatt des batteries lorsqu'elles sont
complètement chargées.
Masse totale : 660 kg
Densité énergétique : 260 W. h. kg-1
Rendement: 86 %.
Ebatt = 660 x260 =1,72 105 Wh.
8.3.7 En tenant
compte du rendement desbatteries, vérifier que l'énergie disponible
vaut E'aM = 1,48 x 102 kW. h à l'entrée des
moteurs.
1,72 105 x0,86 =1,48 105 Wh = 1,48 102
kWh.
8.3.8 Sachant que
les moteurs nécessitent pour fonctionner une puissance d'environ 50 kW,
combien d'heures Solar Impulse 2 peut-il voler sans soleil ? Conclure.
148 /50 ~3 heures.
De nuit, les moteurs peuvent fonctionner pendant 3 heures grâce aux
batteries. Il doit donc, à partir d'une altitude élevée, planer.
|
|
|
|
Partie C. Et si Solar
impulse 2 fonctionnait avec des moteurs thermiques ?
Solar Impulse 2 a été
conçu dans l'optique de montrer qu'il était possible de voler plusieurs
jours d'affilée sans avoir
recours aux énergies fossiles.
C.1 Énergie fossile et combustion
C.1.1 Qu'appelle-t-on énergie
fossile ? Donner au moins une raison qui a poussé les scientifiques à développer le projet
Solar Impulse.
Ce sont les énergies du type charbon, pétrole, gaz naturel, d'origine
fossile, qui ne se renouvellent pas.
Leur combustion contribue à l'effe t de serre ( émission de CO2).
C.1.2 Compléter la chaîne
énergétique du document suivant.
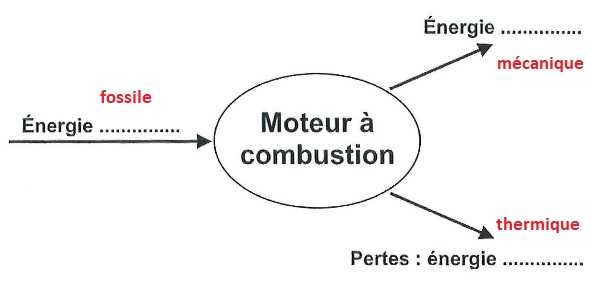
Lors de la
combustion, l'heptane réagit avec le dioxygène pour former du dioxyde
de carbone et de l'eau,
selon l'équation :
C7H16
(l) + ...... O2(g) -->...... CO2 (g) + ...... H2O
(g)
C.1.3 Recopier et ajuster cette
équation sur votre copie.
C7H16
(l) + 11 O2(g) --> 7 CO2 (g) + 8 H2O
(g)
C.1.4 Donner la signification des
pictogrammes relatifs à l'heptane.
Inflammable, toxique pour l'environnement et cancérigène.
C.1.5
Montrer que l'enthalpie standard
de réaction de combustion de l'heptane serait de - 4 796 kJ. mo1-1
.
7 Df H°(CO2)
+8 Df H°(eau) -Df
H°(heptane)=7 x(-393,5) +8x(-285,8) -(245,2) =- 4 796 kJ. mo1-1 .
C.2. Rendement des moteurs à
combustion
L'énergie mécanique
nécessaire à un vol de 48 h est d'environ 9, 0 x 109 J.
C.2.1 Le rendement d'un moteur à
combustion est de l'ordre de 20 %. Calculer l'énergie chimique, Echim qui serait
nécessaire pour que le vol puisse avoir lieu.
Echim = Eméca / rendement = 9,0 109 /
0,20 =4,5 1010 J.
C.2.2.a Montrer que la quantité de
matière, nhept d'heptane nécessaire à un tel vol est d'environ 9, 4 x 103 mol.
4,5 1010 / (4,796 106) =9,38 103~9,4
103 mol.
C.2.2.b Calculer la masse, mhept
d'heptane correspondante.
Mheptane = 100 g/mol ; 100,2 x 9,38 103 =9,399 105
g = 9,399 102 kg ~9,4 102 kg.
C.2.2.c En déduire le volume
d'heptane correspondant.
Masse volumique de l'heptane : 0,68 kg / L.
9,4 102 /0,68 =1,382 103 L ~1,4 103 L.
C.2.3 En utilisant l'équation de
combustion de l'heptane, montrer que la quantité de matière, nc02 , de C02
libérée en 48 h serait de 6, 6 x 104 mol.
7 nhept = 7 x 9,4 103 =6,58 104 ~6,6 104
mol.
C.2.4 Calculer, en tonnes, la masse,
mc02
correspondante.
6,6 104 x MCO2 = 6,6 104 x44 ~2,9 106
g ~2,9 tonnes.
C.3 Crédit carbone - Question ouverte
Le Crédit carbone est
une unité correspondant à une tonne d'équivalent C02 sur les
marchés du
carbone. Combien, selon vous, le voyage de Solar Impulse 2 pourrait-il obtenir de crédit carbone pour son tour
du monde ?
2,9 t pour cette étape.
Le tour du monde s'est effectué en 17 érapes.
Soit 2,9 x17 ~49 t.
|
|
|