Mathématiques,
QCM, nombres complexes
Bac Sti2d et Stl 2015.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Nlle Calédonie.
1. La
négation de la phrase « toute solution de l’équation (E) est
strictement supérieure à 3 » :
a. toute solution
de (E) est inférieure ou égale à 3
b. aucune solution
de (E) n’est strictement supérieure à 3
c. au moins une
solution de (E) est inférieure ou égale à 3. Vrai.
d. une seule
solution de (E) est inférieure ou égale à 3
2. Soient Z1
et Z2 les nombres complexes défini ci-dessous. Une forme
exponentielle du quotient
Z1 / Z2 est :
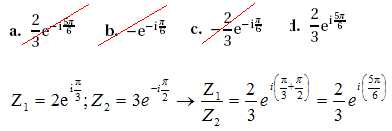
3. On
considère l’équation différentielle y′ +5y = 3, où y désigne une
fonction dérivable sur l’ensemble des réels. La solution f de cette
équation telle que f (0) = 0 est la fonction de la variable x vérifiant
pour tout réel x :
a. f (x) = +0,6e5x
+0,6 ; b. f (x) = −0,6e−5x
+0,6 , vrai; c. f (x) = 0 ; d. f (x) = −3e−5x
+3
Solution générale de y'+5y = 0 : g(x) = A e-5x avec A une constante.
Solution particulière de y'+5y = 3 ; 3 /5.
Solution générale de y' +5y = 3 : f(x) = A e-5x +0,6.
f(0) = 0 = A+0,6 ; A = -0,6.
4. On considère la
production d’une usine de composants électroniques. On admet que la
durée de
fonctionnement sans panne (en années) de ces composants peut être
modélisée par une variable
aléatoire X suivant la loi exponentielle de paramètre l = 0,1.
La probabilité qu’un composant pris au hasard, soit tombé en panne au
bout 6 ans est, au centième
près : a. 1,6 ; b.
0,55, vrai ; c. 0,45 ; d. 0,05.
p(X >=6) = exp(-lt
)= exp(-0,1*6) =exp(-0,6) ~0,549 ~0,55.
Métropole 09/ 2015.
1. On considère le nombre complexe z
= 3 exp(i p/3).
Le nombre complexe conjugué de z est égal à -3 exp(i p/3)
; 3 exp(-i p/3), vrai ; -3
exp(-i p/3) ; 33
exp(i 2p/3).
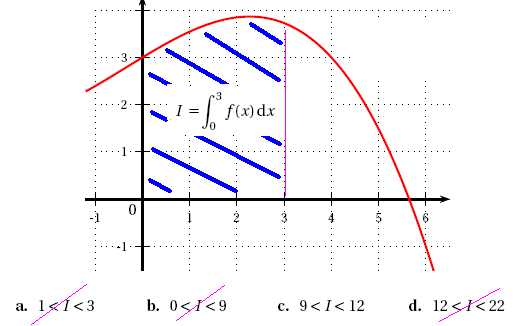
2. La figure
ci-dessous donne la courbe représentative d’une fonction f définie sur
R. On a alors, en unités d’aire :
|
|
|
3. La figure ci-dessous donne la
courbe représentative de la fonction g définie sur [0 ; +∞[ par
g (x)= ln(x2 −2x +4).
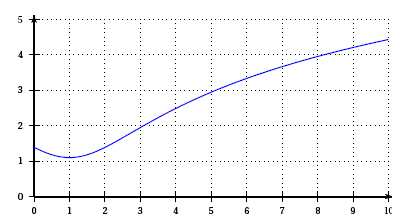
La courbe de la fonction dérivée de la fonction g est :
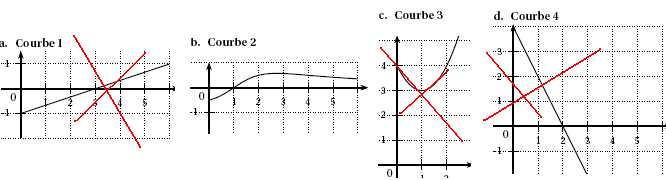
g(x)
décroît de 0 à 1 ( dérivée négative ) , présente un minimum pour
x=1( dérivée nulle ) et croît ensuite ( dérivée positive ).
4. La variable X
suit la loi normale d’espérance 3 et d’écart type 6. La probabilité P(X
< 3) vaut :
a. 3 ; b. 0,5 , vrai ; c. 0 ; d. 0,997.
(3-3) / 6 = 0 ; P(0)
=0,50 ; P(X
< 3) = 0,5.
|
|
Polynésie.
1.
Le plan est rapporté à un repère orthonormé (O, A, B). L’ensemble E des
images des nombres complexes z vérifiant la relation |z| = 1 est
représenté en gras par :
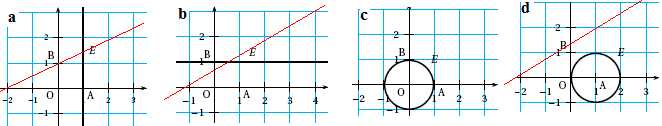
2. Le produit z1
x z2 est égal à :
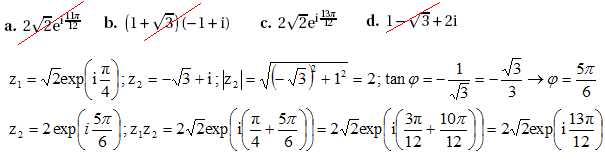
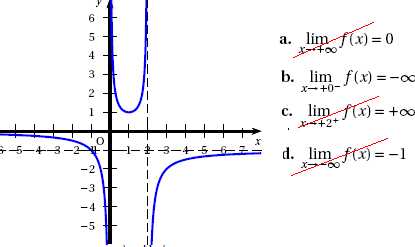
3. Voici
la représentation graphique d’une fonction f . Cette courbe admet les
quatre asymptotes suivantes :
- deux asymptotes horizontales d’équations respectives y = −1 et y
= 0 ;
- deux asymptotes verticales d’équations respectives x = 0 et x =
2. Choisissez la bonne égalité :
4.
On considère l’équation différentielle y′ +2y = 5,(E) où y désigne une
fonction de la variable réelle x dérivable sur R et de dérivée notée
y′. Une solution de cette équation est :
Solution générale de y'+2y =0 ; y = A exp(-2x), avec A une constante.
Solution particulière de (E) y = 2,5. Solution générale de (E) : y = A
exp(-2x) +2,5. Réponse a (
avec A = -0,5). |
|