Mathématiques,
étude de fonctions
Bac Sti2d et Stl 2015.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Nlle Calédonie.
Pour
estimer la quantité dematière nécessaire à la fabrication de la partie
inférieure de l’aileron, l’entreprise souhaite connaître le mieux
possible l’aire A du domaine hachuré.
Pour modéliser le profil
latéral de la partie inférieure on se place dans un repère orthonormé
avec une échelle de 1 carreau pour 10 cm et on se propose d’utiliser,
pour des abscisses comprises entre 0,45 et 3, la courbeCf représentative
de la fonction f définie sur ]0 ; +∞[ par :
f (x) =a / x+b +4ln(x) où a et b sont des constantes réelles qui
restent à déterminer.
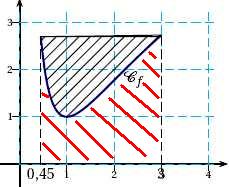
1. Évaluer l’aire A
en nombre entier de carreaux en expliquant votre démarche.
Aire du rectangle de côtés 2,55 x 2,7 - aire hachurée en rouge
~ 6,9 -4,5 ~2,4 carreaux .
2. Déterminer
graphiquement les valeurs de f (1) et de f ′(1).
f(1) = 1 ; f '(1) = 0, tangente horizontale.
3. Vérifier que le
choix de a = 4 et b = −3 répond au problème posé.
f(1) = 4 / 1 -3+4ln 1 = 4-3+0 = 1 ;
f '(x) = -4 / x2+4 / x ; f ' (1) = -4 / 1 +4 /1 =0.
4. Soit la
fonction F définie sur ]0 ; +∞[ par F(x) = (4x +4) ln(x)−7x.
Montrer que F est une primitive de f .
Dériver F : on pose u = 4x+4) et v = ln (x) ; u' = 4 ; v' = 1 / x ;
dérivé d'un produit u'v + v'u = 4 ln (x)+(4x+4) / x = 4 ln (x) +4 +4 /x.
F ' (x) = 4
ln (x)+4 +4 / x-7 = 4 ln(x) -3 +4 / x = f(x).
5.
Déterminer au cm2 près une valeur approchée de l’aire A.
A = 6,9 -[ F(3) -F(0,45) = 6,9 -(16 ln3-21) +5,8 ln 0,45 -3,15.
A = 6,9 -17,58+21 -4,63 -3,15 ~2,54 unités d'aire ou 254 cm2.
Métropole septembre.
Avec
une centaine de décès en moyenne par an, le monoxyde de carbone (CO)
est la première cause de mortalité accidentelle par intoxication en
France.
La société COalerte fabrique un modèle de détecteurs qui
enregistre en temps réel la concentration de monoxyde de carbone en
parties par million (ppm).
Un tel détecteur produit un signal
d’alarme respectant les modalités fixées par la norme européenne EN 50
291 ci-dessous. Il déclenche un signal d’alarme :
• si la concentration est supérieure à 30 ppm pendant au moins 120
minutes ;;
• si la concentration est supérieure à 50 ppm pendant au moins 60
minutes ;
• si la concentration est supérieure à 100 ppm pendant au moins la
minute ;
• si la concentration est supérieure à 300 ppm pendant au moins 3
minutes.
Un
laboratoire d’essais procède à des tests sur un détecteur produit par
la société COalerte en simulant un accident qui provoque une
concentration anormale de monoxyde de carbone dans une pièce.
|
|
|
Partie A.
Le
laboratoire relève la concentration de monoxyde de carbone en fonction
du temps, exprimé en heures. Les enregistrements effectués sur une
période de 8 heures se traduisent par la représentation graphique
ci-dessous.
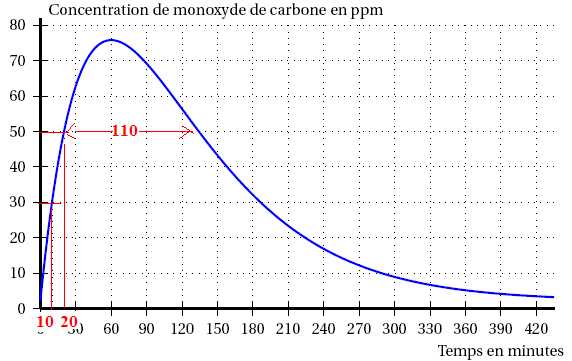
1. Estimer au bout de
combien de temps devrait retentir un signal d’alarme.
Au bout de 10 minutes, la concentration en monoxyde de carbone atteint
30 ppm.
Au
bout de 20 minutes, la concentration en monoxyde de carbone atteint 50
ppm et reste supérrieure à cette valeur pendant plus de 60 min. Un
signal d'alarme va retentir au bout de 60 +20 = 80 minutes.
2.
Une personne présente dans la pièce depuis le début d’un tel accident
risquerait elle de présenter des symptômes ? Si oui, lesquels ?
La
concentration maximale en monoxyde de carbone vaut 75 ppm : céphalée et
nausée chez les enfants ; troubles du rythme cardiaque pour les
personnes atteintes de coronaropathie.
Partie B.
Dans cette partie, tous les résultats seront arrondis à 10−2
près.
La
concentration de monoxyde de carbone exprimée en ppm dans la pièce en
fonction du temps, exprimé en heures, est modélisée par la fonction f
définie sur [0 ; 8] par
f (t )= 2,2+200t e−t .
1. Calculer la
concentration de monoxyde de carbone en ppm dans la pièce :
a. au moment de
l’accident ; f(t=0) = 2,2 ppm.
b. 30 minutes
après. f(t= 0,5) = 2,2 +200*0,5 e-0,5 = 62,85 ppm.
2. À
l’aide du graphique de la partie A, conjecturer les variations de la
concentration de monoxyde de carbone dans la pièce en fonction du temps.
La concentration en monxyde de carbone croït pendant une heure, atteint
un maximum, puis décroît plus lentement.
3. On note f ′ la
fonction dérivée de la fonction f sur l’intervalle [0 ; 8].
a. Montrer que pour
tout réel t de l’intervalle [0 ; 8], f ′(t ) = 200(1−t )e−t .
On pose u = 200 t ; v = e-t ; u' = 200 ; v' = -e-t.
Dérivée d'un produit : u'v +v'u = 200 e-t -200t e-t
; f '(t) = 200 (1-t)e-t.
b. Étudier le signe
de f ′(t ) sur l’intervalle [0 ; 8].
f '(t) s'annule pour t = 1 ; le terme en exponentiel est positif ; f
'(t) est positive sur [0 ; 1[ et négative sur ]1 ; 8].
c. Valider ou
invalider la conjecture émise à la question 2.
La conjecture est validée : fonction croissante si f '(t) positive et
décroissante si f '(t) négative.
4. On note F la fonction définie
sur l’intervalle [0 ; 8] par F(t )= 2,2t −200(t +1)e−t .
On admet que F est une primitive de la fonction f sur l’intervalle [0 ;
8].
Calculer la valeur moyenne de la concentration de monoxyde de carbone
lors des 8 heures qui ont suivi l’accident.
Cmoyen = 1 / 8 { [ F(t)]08 =1 / 8 [2,2 x 8 −200(8 +1)e−8 ]-[2,2
x 0 -200(0+1)e-0] }
Cmoyen
=1 / 8 [17,6 −1800 x 3,35 10-4 ]+200
} =27,12 ppm.
b.
Pour des raisons de sécurité, le ministère du travail fixe un seuil
pour la concentration moyenne de monoxyde de carbone. Ce seuil est de
50 ppm pour une période de 8 heures.
La sécurité des personnes présentes dans la pièce aurait-elle été
remise en cause lors de l’accident simulé ?
27,12 ppm est
inférieure au seuil de 50 ppm : la sécurité des personnes présentes
dans la pièce, n'est pas remise en cause.
|
|
|
|
Antilles Guyanne.
Partie A.
On considère la fonction f définie sur ]0 ; +∞[ par : f (x) = ax +b
ln(x)+1 où a et b sont deux nombres réels.
Cf est la représentation graphique de la fonction f dans un
repère orthonormé.
Les points A et E sont deux points de la courbe Cf . Le
point A a pour coordonnées (1 ; 2) et le point E a pour abscisse 4.
La tangente à Cf au point E est horizontale.
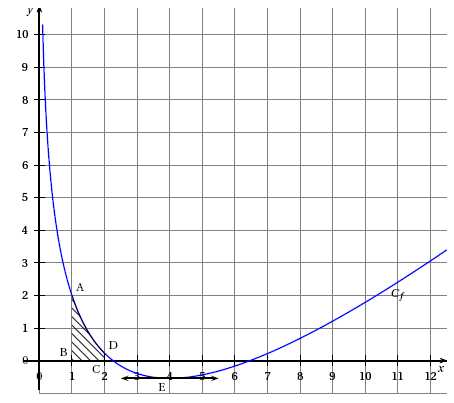
1. Déterminer f
(1) et f ′(4) où f ′ désigne la fonction dérivée de f .
f(1) = 2 ( lecture
graphe ) ; f '(4) = 0,
tangente horizontale).
2. Calculer f ′(x)
puis exprimer f ′(4) en fonction de a et b.
f '(x) = a + b / x ; f '(4) = a +0,25
b = 0.
3. Déterminer les
valeurs de a et b.
f(1) = 2 = a+1 soit a = 1 ;
par suite b = -4.
Partie B .
Soit la fonction f définie sur ]0 ; +∞[ par : f (x) = x −4ln(x)+1
1. Déterminer la limite de f(x) quand x tend vers zéro. Donner
une interprétation graphique du résultat.
x tend vers zéro ; ln (x) tend vers - l'infini ; -4 ln(x) tend
vers plus l'infini.
La droite d'équation x=0 est asymptote à la courbe.
2. Déterminer la
limite de f(x) quand x tend vers l'infini. (on pourra
factoriser l’expression de f (x) par x).
f(x) = x [1-4ln(x) / x +1 /x].
1 / x tend vers zéro ; ln(x) / x tend vers zéro ; f(x) tend donc vers
l'infini.
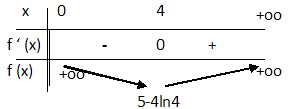
3. Calculer la
dérivée f ′ de f . En déduire le tableau des variations de f .
f '(x) = 1-4 / x.
Partie C.
Une
entreprise fabrique des pièces de carrosserie de voiture. La forme
d’une pièce correspond à la zone hachurée sur le graphique
On souhaite déterminer la mesure de l’aire de la pièce en unité d’aire.
Le point D est le point de la courbe Cf d’abscisse 2. Les
points B et C ont pour coordonnées respectives (1 ; 0) et (2 ; 0).
Soit la fonction G définie sur ]0 ; +∞[ par : G(x) = x ln(x)−x.
1. Calculer la
dérivée G′ de G.
On pose u = x et v = ln(x) ; u'=1 et v' = 1/x ; dérivée d'un produit
u'v +v'u = ln(x) +1 ; G' = ln(x).
2. En déduire une
primitive F de la fonction f donnée dans la partie B sur ]0 ; +∞[.
F = ½x2 -4( x ln(x)−x) +x = ½x2-4
x ln(x) +5x.
3. Déterminer la
valeur exacte de l’aire de la pièce en unité d’aire ; puis en donner
une valeur arrondie à 10−2.
F(2)-F(1) = 0,5 x 4 -4x2ln(2)+10 -(0,5 -0+5) = 12- 8ln(2)-5,5 = 6,5 -8 ln2 ~0,95 unités d'aire.
On étudie la charge d’un condensateur et l’on dispose pour cela du
circuit électrique ci-contre composé de :
• une source de tension continue E de 10 V. • une résistance R de 105
ohms . • un condensateur de capacité C de 10−6 F.
On
note u la tension exprimée en volt aux bornes du condensateur. Cette
tension u est une fonction du temps t exprimé en seconde.
La fonction u est définie et dérivable sur [0 ; +∞[ ; elle vérifie
l’équation différentielle suivante :
RCu′ +u = E où u′ est la fonction dérivée de u.
1. Justifier que
l’équation différentielle est équivalente à : u′ +10u = 100 (E).
RC = 105 x 10-6 = 0,1.
0,1 u' + u = 10 ; u' +10 u = 100.
2. a. Déterminer la
forme générale u(t ) des solutions de cette équation différentielle.
Solution générale de u'+10 u =0 : u = A zxp(-10t) avec A une
constante.
Solution particulière de (E) u = 10.
Solution générale de (E) : u = A
exp(-10 t) +10.
b.
On considère qu’à l’instant t = 0, le condensateur est déchargé. Parmi
les solutions, déterminer l’unique fonction u tel que u(0) = 0.
u(0) = 0 = A+10 ; A = -10 ; u(t) = 10
( 1-exp(-10t)).
c. Déterminer en
justifiant la réponse, la limite en +∞de la fonction u ainsi obtenue.
En donner une interprétation.
Le terme en exponentielle tend vers zéro si le temps devient très long.
u(t) tend vers 10 : le condensateur est chargé complètement.
3. On
donne ci-contre la représentation graphique de la fonction u qui vient
d’être obtenue à la question 2. b. avec les unités suivantes : 1 unité
pour 1 seconde sur l’axe des abscisses et 1 unité pour 1 volt sur l’axe
des ordonnées.
On appelle T le temps de charge en seconde pour que u(T ) soit égal à
95% de E.
a. Déterminer
graphiquement le temps de charge T .
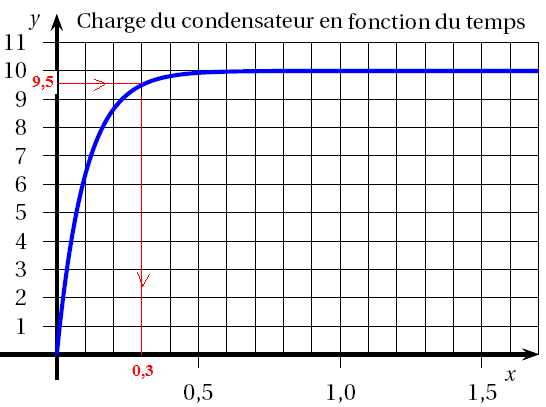
b. Retrouver, par
le calcul, le résultat précédent.
9,5 = 10 ( 1-exp(-10T)) ; 0,95 = 1-exp(-10T) ; exp(-10T) = 0,05 ; -10T
= ln(0,05) ; T ~0,3 s.
4.
Sans modifier les valeurs respectives de E et de C, déterminer la
valeur de R afin que le temps de charge T soit multiplié par 2.
exp(-2T/(RC)) = 0,05 ;-2T / (RC) = ln 0,05 ; RC = -2T / ln (0,05) =-0,6
/ ln(0,05) ~0,20 ; R = 0,2 / 10-6 = 2 105 ohms.
|
|
Métropole.
Une
fibre optique est un fil très fin, en verre ou en plastique, qui a la
propriété d’être un conducteur de la lumière et sert dans la
transmission d’un signal véhiculant des données.
La puissance du signal, exprimée en milliwatts (mW), s’atténue au cours
de la propagation. On note PE et PS les
puissances respectives du signal à l’entrée et à la sortie d’une
fibre. Pour une fibre de longueur L exprimée en kilomètres (km), la
relation liant PE , PS et L est donnée par : PS
= PE x e−aL
où a est le coefficient d’atténuation linéaire dépendant de la fibre.
Une entreprise utilise deux types de fibre optique de coefficients
d’atténuation différents.
Dans tout l’exercice :
- la puissance du signal à l’entrée de la fibre est 7mW ;
- à la sortie, un signal est détectable si sa puissance est
d’aumoins 0,08 mW ;
- pour rester détectable, un signal doit être amplifié dès que sa
puissance devient strictement inférieure à 0,08 mW.
Partie A.
Le premier type de fibre de longueur 100 km utilisé par l’entreprise a
un coefficient d’atténuation linéaire a = 0,046.
Pour
ce type de fibre, sera-t-il nécessaire de placer au moins un
amplificateur sur la ligne pour que le signal soit détectable en sortie
?
PS = 7 x
exp(-0,046 x 100) =0,070 mW,
valeur inférieure à 0,08 mW : le signal doit être amplifié.
Partie B.
La
puissance du signal le long du second type de fibre est modélisée par
une fonction g de la variable x, où x étant la distance en kilomètres
parcourue par le signal depuis l’entrée de la fibre.On admet que cette
fonction g est définie et dérivable sur l’intervalle [0 ; +∞[ et
qu’elle est solution sur cet intervalle de l’équation différentielle y′
+0,035y = 0.
1. Résoudre
l’équation différentielle y′ +0,035y = 0.
g(x) = A exp(-0,035 x)
avec A une constante.
2. a. Sachant que g
(0) = 7, vérifier que la fonction g est définie sur l’intervalle [0 ;
+∞[ par g (x) = 7exp(−0,035x).
g(0) = A exp(0) = 7 ; A = 7 et g(x) = 7
exp(-0,035 x).
b.
En déduire le coefficient d’atténuation de cette fibre. 0,035.
3. a. Étudier le
sens de variation de la fonction g .
g'(x) = 7 x(-0,035) exp(−0,035x) =
-0,245 exp(−0,035x) ; la dérivée
est négative sur l'intervalle d'étude, g(x) est strictement
décroissante.
b.
Déterminer la limite de la fonction g en +∞.
Le terme en exponentielle tend vers zéro ; g(x) tend vers zéro.
4. a. Le signal
sera-t-il encore détecté au bout de 100 km de propagation ?
g (100) = 7exp(−0,035 x
100)= 7 exp ( -3,5) = 0,211 mW,
valeur supérieure à 0,08 mW : le signal est détecté.
b.
Déterminer la longueur maximale de la fibre permettant une détection du
signal à la sortie sans amplification.
g(x) >=0,08 ; 7exp(−0,035x)
>= 0,08 ; exp(−0,035x)
>=0,011482 ; -0,035 x >= ln 0,01142857 ; -0,035 x >= -4,4716 ; x < 127,76 km.
Polynésie.
Un
pont à une seule arche d’une longueur de 16 m enjambe une route à
double circulation. La figure ci-dessous donne une vue de l’une des
deux façades de ce pont (1 unité
représente 1 mètre). La partie
supérieure du pont est à une hauteur de 5m au-dessus de la route. La
partie de l’axe des abscisses comprise entre -8 et 8 représente la
chaussée sur
laquelle sont délimitées les zones de circulation des piétons, des
cyclistes et des véhicules motorisés.
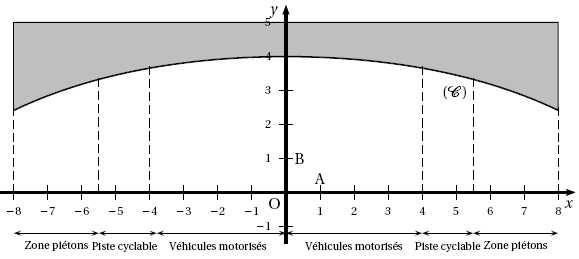
A– Étude de la
fonction représentée par la courbe(C )
Soit la fonction f définie, pour tout réel x de l’intervalle [−8 ; 8],
par f (x) = k −0,5[e0,2x +e−0,2x ] où k désigne
un entier naturel fixé.
On note (C ) sa courbe représentative, donnée ci-dessus dans le repère
orthonormé (O, A, B).
1. Déterminer
graphiquement f (0). En déduire que pour tout réel x de l’intervalle
[−8 ; 8] : f (x) = 5−0,5[e0,2x +e−0,2x ].
f(0) = 4 = k-0,5 [e0 +e-0] =k-0,5(1+1) = k-1 ; k = 5.
2.
En tenant compte du fait que l’on doit laisser une hauteur de sécurité
de 50 cm, quelle doit être la hauteur maximale exprimée en mètre d’un
véhicule motorisé pour qu’il puisse passer sous le pont ? On arrondira
le résultat à 10−1.
f(4) = 5-0,5[e0,8 +e-0,8] =5-0,5 [ 2,226 +0,4493]
=3,66 m ; retirer 0,5 m d'où :
3,2 m.
3. Montrer que la
fonction f ′ dérivée de la fonction f est définie, pour tout réel x de
l’intervalle [−8 ; 8], par f ′(x) = 0,1e−0,2x (1−e0,4x
).
f '(x) = 0-0,5(0,2 e0,2x
-0,2e−0,2x ) = -0,1 (e0,2x -e−0,2x) = 0,1 (e-0,2x
-e+0,2x) = 0,1e−0,2x
(1−e0,4x ).
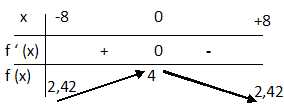
4.
Étudier le signe de f ′(x) sur [−8 ; 8]. En déduire le tableau de
variation de f sur [−8 ; 8].
0,1e−0,2x est
positif ; 1-e−0,4x s'annule
pour x = 0 ; 1-e−0,4x est
positif pour x appartenant à ]-8 ; 0[ et négatif pour x appartenant à
[0 ; 8[.
B– Calculs d’aires
La façade du pont est la partie grisée représentée sur la figure
précédente.
1. Calculer la
valeur exacte de l’intégrale I .
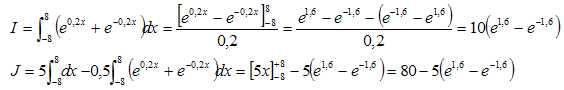
2. Vérifier que
l’aire de la façade exprimée en m2 vaut 5(e1,6 −e−1,6).
16 x 5 - J = 5(e1,6 −e−1,6).
3.
On veut peindre les deux façades du pont. En déduire l’aire S exprimée
en m2 de la surface totale à peindre ; en donner une valeur
en m2 approchée à 10−2 près.
2 x 5 (4,953 -0,2019) = 47,51 m2.
4.
La peinture utilisée pour peindre les façades du pont est vendue par
bidon de 5 litres. Sachant que cette peinture a une propriété de
recouvrement de 3 m2 par litre, combien de bidons sont
nécessaires pour recouvrir les deux faces de cette construction ?
47,51 / (3 x 5) =3,17 soit 4 bidons.
|
|