Mathématiques,
QCM, pourcentages, suites numériques
Bac St2S 2014.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie.
On présente dans un
tableau, extrait d’une feuille de calcul, le nombre de cartes SIM(carte
électronique permettant d’utiliser un réseau de téléphonie mobile avec
un téléphone mobile) en service en France métropolitaine.
|
A
|
B
|
C |
D
|
E
|
F
|
G
|
H
|
1
|
|
Juin
2010
|
Décembre
2010
|
Juin
2011
|
Décembre
2011
|
Juin
2012
|
Décembre
2012
|
Juin
2013
|
2
|
Nombre
de cartes SIM ( en millions )
|
62,1
|
65
|
66
|
68,6
|
|
73,1
|
74,8
|
3
|
Taux
d'évolution semestriel
|
|
4,7
%
|
|
3,9
%
|
4,8%
|
|
|
Source : ARCEP
1. a. Calculer le
nombre de cartes SIM, arrondi au dixième de million, en service en
France métropolitaine en juin 2012.
Soit x ce nombre : ( x-68,6) /68,6 = 0,048 ; x=68,6 = 68,6 x0,048 =
3,2928 ; x = 68,6 +3,2928 ~71,9.
b. Calculer le taux
d’évolution, du nombre de cartes SIM en service en France
métropolitaine entre décembre 2012 et juin 2013.
(74,8-73,1) / 73,1 x100 ~2,3 %.
c. Les cellules de
C3 à H3 sont au format pourcentage avec une seule décimale. Donner une
formule qui, entrée dans la cellule C3, permet par recopie les taux
d’évolution semestriels dans la plage de cellules C3 : H3.
=(C2-B2) / B2
2. On suppose qu’à
partir de juin 2013 le nombre de cartes SIM en service en France
métropolitaine augmente chaque semestre de 3%.
On note un le nombre de cartes SIM en service en France métropolitaine,
exprimé en millions, à la fin du n-ième semestre après juin 2013. On
définit ainsi la suite (un) avec u0 = 74,8 et u1
est le nombre de cartes SIMen service en France métropolitaine en
décembre 2013.
a. Montrer que la
suite (un) est géométrique et déterminer sa raison.
L'élément de rang n+1 est obtenu en multipliant l'élément de rang
n par le nombre 1,03.
Chaque élément est obtenu en multipliant le précédent par 1,03. La
suite est géométrique de raison q = 1,03.
b. Exprimer un
en fonction de n.
un = u0 x 1,03n= 74,8 x1,03n.
c. Calculer u4 . Donner
son arrondi au dixième de million et interpréter le résultat.
u4 = 74,8 x1,034 = 84,2.
En juin 2015, le nombre de carte SIM en service en France est
égal à 84,2 millions.
d. Résoudre
l’inéquation : 74,8×1,03n >100. Interpréter le résultat.
log 74,8 + n log 1,03 > log 100 ; n log 1,03 > log100 -log 74,8 ;
n > 0,126 / log 1,03 ; n >9,8.
En juin 2018, le nombre de carte SIM en service en
France est supérieur à 100 millions.
QCM.
1. La fonction g
est définie sur l’intervalle [0 ; 100] par : g (x) = 4×0,7x+1
. On a alors :
a. g (2) = 2,96 ; b. g (2) = 21,952 ; c. g (2) = 1,372 vrai ; d. g (2)= 8,84.
g(2) = 4 x0,73 = 1,372.
2. La fonction h
est définie sur l’intervalle [0 ; 5] par : h(x) = x3 −6x2
−15x +3. La fonction h est dérivable sur l’intervalle [0 ; 5] et on
note h′ sa fonction dérivée. On a :
a. h′(x) = (3x
+3)(x −5) vrai ; b. h′(x) = 3x2 −6x +3 ; c. h′(x) = 3x2 −12x +3 ; d. h′(x) = −15x −15.
h'(x) = 3x2 -12x-15 =3 (x+1)( x-5).
3.
La fonction m est définie sur [1 ; 9]. On suppose que m est dérivable
sur l’intervalle [1 ; 9] et on note m′ sa fonction dérivée avec :
m′(x) = −2x +6 . On en déduit que :
a. La fonction m
est décroissante sur [1 ; 9] ; b.
La fonction m est croissante sur [1 ; 9]
c. La fonction m
est décroissante sur [1 ; 3] ; d.
La fonction m est croissante sur [1 ; 3], vrai.
m'(x) est positive sur [1 ; 3 [ : m(x) est strictement croissante
sur cet intervalle.
m'(x) est négative sur ]3 ; 9 ] :
m(x) est strictement décroissante sur cet intervalle.
m'(x) = 0 pour x = 3 ; m(x) présente un maximum pour x = 3.
4.
On donne les représentations graphiques de 4 fonctions définies sur
l’intervalle [0 ; 4] . On suppose que chacune de ces fonctions est
dérivable sur l’intervalle [0 ; 4] . Laquelle admet la droite
d’équation y = 2x +1 comme tangente en un point de sa courbe
représentative ?
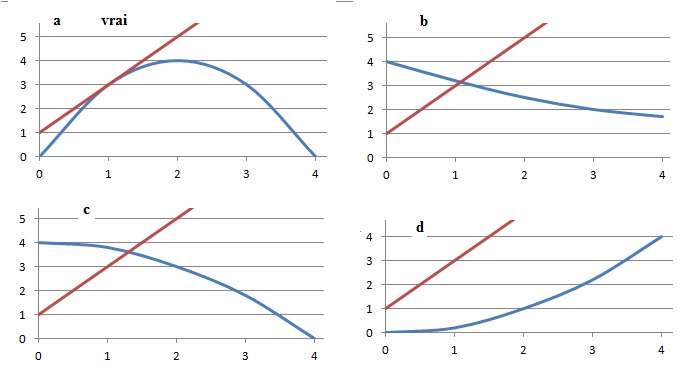
|
|
|
Métropole
On
mesure la fréquence cardiaque d’un athlète courant sur un tapis roulant
dont la vitesse peut être modifiée. Les résultats sont donnés dans le
tableau ci-dessous.
Vitesse
de course xi ( km / h)
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
Fréquence
cardiaque yi ( battements par minute)
|
128
|
134
|
139
|
145
|
150
|
156
|
163
|
1. a. Représenter
le nuage de points de coordonnées (xi ; yi ).
b. Déterminer les
coordonnées du point moyen G de ce nuage de points et le placer. Que
remarque-t-on ?
xG=(12 +13 +14 +15 +16 +17 +18) / 7=15
yG=(128 +134 +139 +145 +150 +156 +163) / 7 =145.
G est confondu avec l'un des points du nuage.
c. Pour estimer la
fréquence cardiaque de l’athlète à des vitesses de course plus élevées,
on utilise un ajustement affine de ce nuage de points.
On admet que la droite (D) d’équation : y = 5,7x +59,5 réalise un tel
ajustement. Tracer la droite (D).
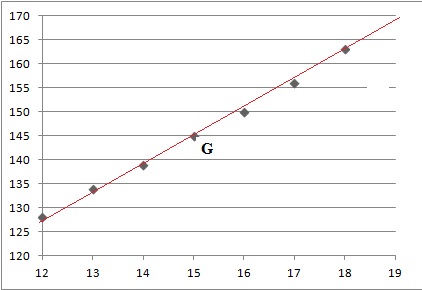
2. La fréquence
cardiaque maximale est le nombre maximal de battements que le coeur est
en mesure d’effectuer en une minute. Pour un individu d’âge N, cette
fréquence, habituellement notée Fcmax, est donnée par : Fcmax
= 220−N.
Dans les questions suivantes, les résultats seront arrondis à l’unité.
En utilisant l’ajustement affine précédent :
a. calculer la
fréquence cardiaque de l’athlète pour une vitesse de course de 20 km.h−1
;
f = 5,7 x20 +59,5 = 173,5 ~174.
b. déterminer
jusqu’à quelle vitesse pourra aller l’athlète, sachant qu’il a 35 ans ;
justifier la réponse.
fcmax
= 220-35 =185.
185 = 5,7 x +59,5 ; 5,7 x = 185-59,5 = 125,5 ; x = 125,5 / 5,7 = 22
km/h.
QCM
1. La suite (un)
est une suite arithmétique telle que : u1 = −10 et u6
= 8. Sa raison est égale à :
A. 3 ; B. −3 ; C. 3,6, vrai ; D. −3,6.
u6 = u1 +5 r ; 5r = 8-(-10) = 18 ; r = 18 /5 =
3,6.
2. La suite (un)
est une suite arithmétique de raison −15 et telle que u1 =
1000.
Le premier entier naturel n tel que un inférieur ou égal à
250 est :
A. 49 ; B. 50 ; C. 51, vrai ; D. 52.
un = u1 + (n-1) r ; n-1= (un-u1)
/ r ; n =1+
(un-u1) / r = 1 +(250-1000)/(-15).
n=51. A partir du terme de rang 51, un est inférieur ou égal à 250.
3.
On sait que la population d’une ville était de 235 000 habitants le 1er
janvier 2013 et que cette population augmente de 1,5% par an. Le 1er
janvier 2020, une estimation de la population de cette ville, arrondie
à l’unité, sera de :
A. 260814, vrai ; B. 264726 ; C. 625105; D. 4015195.
Suite géométrique de raison q = 1,015 et de premier terme u0
= 235000.
u7 = u0 q7 = 235000 x1,0157
= 260814.
4. Dans le tableau
ci-dessous, extrait d’une feuille de calcul automatisé, se trouve le
premier terme u1 d’une suite géométrique (un) de
raison 0,8. On a u1 = 150.
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
2
|
150
|
|
|
|
|
|
La
formule à entrer dans la cellule B2, destinée à être recopiée vers la
droite jusqu’à la cellule F2 et qui permet d’afficher les termes
suivants de cette suite, est :
A. =$ A2*0,8 ; B. =A2*0,8 vrai ; C. =150*$A1 ; D. =A2*0,8^A1.
5. Le tableau
ci-dessous résume une partie des informations concernant les pratiques
artistiques et sportives de 400 élèves d’un lycée.
Nombre
d'élèves...
|
pratiquant
une activité artistique
|
ne
pratiquant pas d'activité artistique
|
Total
|
pratiquant
un sport
|
90
|
150
|
240
|
ne
pratiquant pas de sport
|
90
|
70
|
160
|
Total
|
180
|
220
|
400
|
On choisit un élève de ce lycée au hasard.
a. La probabilité
que l’élève choisi pratique un sport et une activité artistique est :
A. 90 ; B. 0,175 ; C. 0,225, vrai ; D. 0,825.
90 / 400 = 0,225.
b. Sachant qu’un
élève pratique un sport, la probabilité qu’il pratique une activité
artistique est :
A. 0,375, vrai ; B. 0,45 ; C. 0,225 ; D. 0,825.
90 / 240=0,375
c. La probabilité
qu’un élève de ce lycée choisi au hasard pratique un sport ou une
activité artistique est :
A. 0,375 ; B. 0,175 ; C. 0,325 ; D. 0,825, vrai.
(240 +180 -90 ) /400 =0,825
|
|
|
|
Antilles.
Le tableau ci-dessous donne le nombre de maladies professionnelles
ayant entrainé un arrêt de travail de 2003 à 2010 :
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
Année
|
2003
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2
|
Rang
de l'année xi |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
3
|
Nombre
de maladies professionnelles yi
|
34600
|
36900
|
41300
|
42300
|
43800
|
45400
|
49300
|
50700
|
Source : Caisse Nationale d’assuranceMaladie des Travailleurs Salariés
1. Représenter le nuage de points de coordonnées (xi, yi).
2. a. Déterminer
les coordonnées exactes du point moyen G de ce nuage de points.
b. Placer le point
G sur le graphique précédent.
xi=(1 +2 +3 +4 +5 +6 +7 +8 ) / 8 =4,5.
yi=(32600 +36900 +41300 +42300 +43800 +45400 +49300 +50700)
/8=43037,5.
3. On considère que la droite (D) d’équation y = 2244x +32939,5,
réalise un ajustement du nuage de points.
a. Vérifier par le
calcul que le point G appartient à la droite (D).
b. Tracer la droite
(D) sur le graphique précédent.
2244 x4,5 +32939,5=43037,5 =yG.
Les coordonnées de G vérifient l'équation de la droite (D). G
appartient à cette droite.
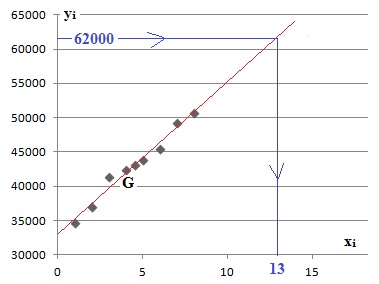
4. Déterminer par
le calcul le nombre de maladies professionnelles ayant entrainé un
arrêt de travail prévu par l’ajustement de la question 3. en 2014 ? (
On donnera le résultat arrondi à la centaine).
Rang de l'année 2014 : x=12 ; y = 2244 x12 + 32939,5=59867,5 ~59900.
5. a. En utilisant
le graphique, déterminer l’année, à partir de laquelle l’ajustement de
la question 3. prévoit que l’on dépassera 62 000 maladies
professionnelles ayant entrainé un arrêt de travail.
b. Retrouver par un
calcul, le résultat de la question 5.a.
2244x +32939,5 >62000 ; 2244 x > 62000-32939,5 ; 2244 x >
29060,5 ; x >29060,5 / 2244 ; x >12,95.
( x >13). en 2015 on dépassera 62000 maladies professionnelles
ayant entraînées un arrêt de travail.
Le tableau ci-dessous, extrait d’une feuille de tableur, donne
l’évolution du nombre de mariages en France de 2007 à 2011.
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
Année
|
2007
|
2008
|
2009
|
2010
|
2011
|
2
|
Nombre
de mariages
|
273669
|
265404
|
251478
|
251654
|
236826
|
3
|
taux
d'évolution par rapport à l'année précédente
|
|
-3,02%
|
-5,25%
|
0,07
%
|
-5,89
%
|
Source : INSEE, estimations de population-statistiques de l’état civil
On précise que les
cellules C3 à F3 ont au format pourcentage avec deux décimales.
1. Une formule a
été saisie dans la cellule C3 puis recopiée vers la droite jusqu’à la
cellule F3 pour calculer le tauxd’évolution du nombre demariages en
France entre deux années consécutives de 2007 à 2011.
Parmi les formules ci-dessous, une et une seule est exacte.
a.
=(C2-B2)/C2 ; b. =C2/B2 ; c.
=(C2-$ B2)/$ B2 ; d.
=(C2-B2)/B2 . Vrai.
Recopier la réponse choisie sur la copie.
2. Montrer que le
nombre de mariages en France a baissé d’environ 13,46% entre 2007 et
2011.
(236826 - 273669) / 273669 x100 = -13,46 %.
3.
On considère qu’à partir de 2011, le nombre de mariages continue à
baisser chaque année de 3,55%. Pour tout entier n positif ou nul, on
note un le nombre de mariages en France pour l’année
(2011+n). Ainsi u0 = 236826.
a. À l’aide de ce
modèle, estimer le nombre de mariages en France en 2012.
u1=u0 x(1-0,0355)=0,9645 u0=0,9645 x
236826=228419.
b. Justifier pour
tout entier n l’égalité : un+1 = 0,9645×un.
c. En déduire la
nature de la suite (un) et préciser sa raison.
d. Pour tout entier
n, exprimer un en fonction de n.
Chaque élément est obtenu en multipliant
le précédent par 0,9645. La
suite est géométrique de raison q = 0,9645
un = 0,9645n u0.
e. Selon ce modèle,
à partir de quelle année le nombre de mariages en France deviendrait-il
inférieur à 200 000 ?
0,9645n u0 <
200000 ; n log 0,9645 + log u0 < log 200000 ;
-0,0157 n + 5,374 < 5,301 ; -0,0157 n < -0,073 ; n >0,073 /
0,0157 ; n > 4,6 ; on retient x = 5 ( année 2016 ).
|
|
Antilles septembre.
L’indice de masse corporelle d’une personne (IMC) se calcule grâce à la
formule suivante : IMC = Masse / (Taille)2 dans laquelle
lamasse est exprimée en kilogramme et la taille en mètre.
On précise qu’une personne est en surpoids si son IMC est supérieur ou
égal à 25.
On a demandé à un groupe de 10 élèves de donner leur masse et leur
taille. Les données ont ensuite été consignées dans une feuille
automatisée de calcul reproduite ci-dessous :
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
1
|
Elève
n°
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
2
|
Masse
( kg)
|
54
|
65
|
64
|
70
|
72
|
61
|
64
|
76
|
45
|
78
|
3
|
Taille
(m)
|
1,73
|
1,84
|
1,65
|
1,62
|
1,70
|
1,74
|
1,86
|
1,57
|
1,60
|
1,71
|
4
|
IMC
|
18,0
|
19,2
|
23,5
|
26,7
|
24,9
|
20,1
|
18,5
|
30,8
|
17,6
|
26,7
|
La ligne 4 est au format nombre
avec une décimale.
1. Quelle formule a
été saisie dans la cellule B4 puis recopiée vers la droite jusqu’à la
cellule K4 pour calculer l’IMC des 10 élèves ?
=B2/(B3*B3)
2. Quelle est la
proportion d’élèves en surpoids dans ce groupe ? On exprimera le
résultat en pourcentage.
3 élèves sur 10 sont en surpoids soit 3 *100 / 10 = 30 %.
En 2012, en France, on
comptait une proportion d’hommes d’environ 47,5%.
Environ 42% des femmes et 54% des hommes étaient en surpoids. (source :
rapport OBEPI 2012)
On choisit une personne au hasard dans la population française, chaque
personne ayant la même probabilité d’être choisie.
On désigne par les lettres F, H et S les évènements suivants :
F : « la personne choisie est une femme »
H : « la personne choisie est un homme »
S : « la personne choisie est en surpoids »
1. a. Donner la
probabilité que la personne choisie soit une femme. On note P(F) cette
probabilité.
p(F) = 1-0,475 = 0,525.
b. Donner la
probabilité que la personne choisie soit en surpoids sachant que c’est
un homme.On note PH (S) cette probabilité.
PH (S)=0,54.
2.
Compléter l’arbre des probabilités donné dans l’annexe, à rendre avec
la copie.
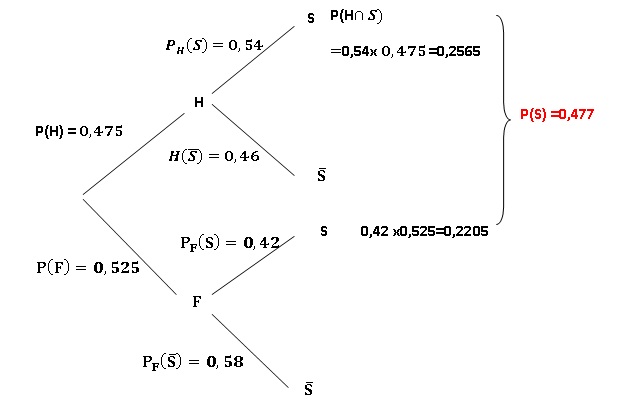
a. Décrire par une
phrase l’événement suivant H ∩S. et calculer sa probabilité.
La personne est un homme en surpoids.P(H ∩S) = 0,2565
~0,26.
3. Montrer que :
P(S)= 0,477.
4. Les évènements S
et H sont-ils indépendants ? Justifier la réponse.
P(H) x P(S) = 0,475 x 0,477 = 0,2266, valeur différente de P(H ∩S). Les
évenements S et H ne sont pas indépendants.
5. Calculer la
probabilité de choisir un homme sachant que la personne choisie est en
surpoids. On donnera le résultat arrondi à 0,001 près.
PS(H) = P(H ∩S) / P(S)
=0,2565 / 0,477 ~0,538.
Le tableau ci-dessous donne la population française, hors Mayotte, de
l’année 2004 à l’année 2013.
Année
|
Rang
de l'année ( xi)
|
Population
( yi) en milliers
|
2004
|
1
|
62251
|
2005
|
2
|
62731
|
2006
|
3
|
63186
|
2007
|
4
|
63601
|
2008
|
5
|
63962
|
2009
|
6
|
64305
|
2010
|
7
|
64613
|
2011
|
8
|
64949
|
2012
|
9
|
65281
|
2013
|
10
|
65586
|
Source : INSEE (en 2011, 2012
et 2013, les données sont provisoires)
On donne, en annexe, le nuage de points Mi (xi ; yi
).
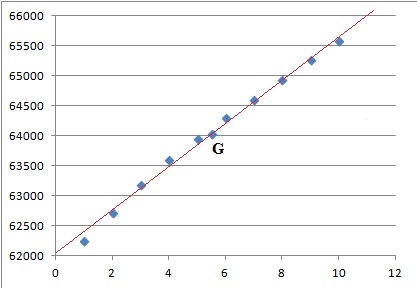
1. a. Montrer que
les coordonnées du point moyen G du nuage de points sont (5,5 ;
64 046,5), puis placer G sur le graphique.
xi =(1+2+3+4 +5+6+7 +8+9+10) /10=5,5.
yi = (62251 +62731 +63186 +63601 +63962 +64305 +64613 +64949
+65281 +65586) / 10 =64046,5.
b. On admet que la
droite D de coefficient directeur 364 passant par le point G constitue
un ajustement du nuage de point .
Montrer que l’équation réduite de la droite D est : y = 364x +62044,5.
La droite d'équation y = 364 x+b passe par G( 5,5 ; 64046,5) : 64046,5
= 364 x5,5 +b, d'où b =62044,5.
c. Tracer la
droite D sur le graphique.
2. En utilisant
l’ajustement précédent, déterminer par le calcul, une estimation de la
population française hors Mayotte, en 2015.
x = 12 ; y = 364 x12 +62044,5 = 66412,6 en milliers d'habitants.
En quelle
année, selon l’ajustement de la question 1. b., la population
française, hors Mayotte, dépasserait-elle 67 000 milliers d’habitants ?
364x +62044,5 > 67000 ; 364 x > 67000-62044,5 ; 364 x
>4955,5 ; x > 4955,5 / 364 ; x >13,6. x = 14, année 2017.
Nlle Calédonie.
Le tableau suivant donne l’évolution du nombre d’interruptions
volontaires de grossesse (I.V.G.)médicamenteuses dans les villes des
départements d’outre-mer de 2005 à 2011.
Année
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
Rang
(xi)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Nombre
d'IVG médicamenteuse (yi)
|
543
|
952
|
1338
|
1642
|
1967
|
2467
|
2511
|
Source : DREES,Ministère des
affaires sociales et de la santé
1. Calculer le
taux d’évolution du nombre d’I.V.G.médicamenteuses entre 2010 et 2011.
Arrondir le résultat à 0,1%.
(2511-2467) / 2467 x100 =1,78 ~1,8 %.
2. Représenter sur
une feuille de papiermillimétré le nuage de points.
3. Déterminer les
coordonnées du point moyen G de ce nuage de points. On arrondira
l’ordonnée de G à l’entier.
xi =(1 +2 +3 +4 +5 +6 +7) / 7 =4.
yi=(543 +952 +1338 +1642 +1967 +2467 +2511) / 7 ~1631.
Dans toute la suite de l’exercice, on prendra pour coordonnées de G(4 ;
1 631).
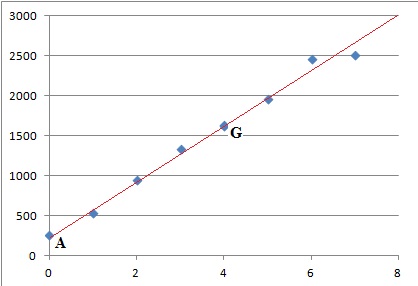
4. Soit le point
A(0 ; 265).
a. Tracer la
droite (AG) sur le graphique du nuage de points
b. Montrer que la
droite (AG) a pour équation : y = 341,5x +265.
La droite d'équation y = ax+b passe en A ; 265= 0 +b.
La droite passe en G : 1631 = 4a +265 d'où a = (1631-265) / 4 = 341,5.
5. On admet que la
droite (AG) est un ajustement affine pertinent du nuage de points qui
permet d’effectuer des estimations au-delà de 2011. En utilisant cet
ajustement affine, calculer :
a. le nombre
d’I.V.G.médicamenteuses dans les villes des départements d’outremer en
2014 ;
x = 10 ; y = 3415+265 = 3680.
b. l’année à partir
de laquelle le nombre d’I.V.G. médicamenteuses dans les villes des
départements d’outre-mer dépassera 4 500.
341,5x +265 > 4500 ;
341,5 x > 4235 ; x > 4235 / 341,5 ; x >12,4 ; x = 13, année
2017.
Chaque année on déplore des accidents de la route mortels (c’est-à-dire
ayant entraîné un décès au moins).
Le tableau ci-dessous indique le nombre de conducteurs de voiture de
tourisme impliqués dans un accident mortel en 2011, en fonction de leur
alcoolémie et du port
de la ceinture de sécurité.
|
Test
d'alcoolémie positif
|
Test
d'alcoolémie négatif
|
Total
|
Nombe
de conducteurs ceinturés
|
383
|
2185
|
2568
|
Nombre
de conducteurs non ceinturés
|
167
|
92
|
259
|
Total
|
550
|
2277
|
2827
|
Source : ONISR, Fichier des accidents
Dans les questions suivantes, les résultats seront donnés sous forme
décimale et arrondis au millième.
On prélève au hasard le dossier d’un conducteur parmi les 2 827
conducteurs impliqués dans des accidents mortels.
On considère les évènements suivants :
A : « Le test d’alcoolémie du conducteur était positif au moment de
l’accident » ;
C : « Le conducteur était ceinturé au moment de l’accident ».
1. Calculer la
probabilité que le test d’alcoolémie du conducteur ait été positif au
moment de l’accident.
P(A) =550 / 2827 ~0,195.
2. Calculer la
probabilité que le conducteur n’ait pas été ceinturé au moment de
l’accident.
259 / 2827 ~ 0,092.
3. a. Décrire par une phrase l’évènement suivant.et montrer que sa
probabilité est environ égale à 0,227.
Le conducteur n'était pas ceinturé ou bien le test d'alcoolémie
était positif.
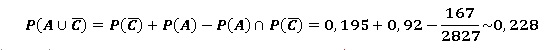
4. a. Quelle est la probabilité que le
conducteur n’ait pas été ceinturé, sachant que son test d’alcoolémie
était négatif ?
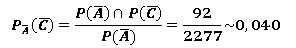
b. Calculer la
probabilité suivante.
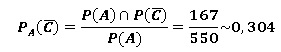
c. Comparer ces
deux derniers résultats et commenter par une phrase.
En buvant, on oublie de mettre la ceinture.
|
|