Mathématiques,
probabilités
Bac St2S 2014.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie.
Partie A.
Les résultats d’une étude concernant le nombre de personnes d’une
commune ayant attrapé la grippe entre 2007 et 2012 sont donnés dans le
tableau ci-dessous.
Année
|
2007
|
2008 |
2009
|
2010
|
2011
|
2012
|
Rang
de l'année (xi)
|
1
|
2
|
3
|
4
|
5
|
6
|
Nombre
de personnes ( yi)
|
618
|
601
|
605
|
600
|
597
|
591
|
1.a Représenter le nuage de points
associé aux données du tableau précédent de coordonnées (xi
; yi ).
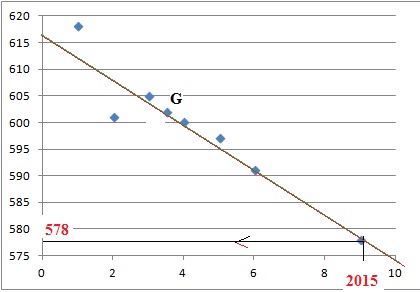
b. Calculer les
coordonnées du point moyen G de ce nuage de points et placer G dans le
repère précédent.
xG = (1 +2 +3 +4 +5 +6) / 6= 3,5.
yG = (618 +601 +605 +600 +597 +591) / 6 =602.
2. On considère la
droite (D) d’équation : y = −4,3x +617,05. On admet que la droite (D)
réalise un ajustement affine du nuage de points, valable jusqu’en 2015.
a. Le point G
appartient-il à la droite (D) ? Justifier.
-4,3 x3,5 +617,05 = 602=yG.
Les coordonnées du point G vérifient l'équation de (D) : G appartient à
cette droite.
b. Tracer la droite
(D) dans le repère précédent.
c. Déterminer
graphiquement puis par le calcul une prévision du nombre de personnes
qui auront la grippe en 2015. Pour la lecture graphique, on laissera
apparent les traits de construction.
Pour 2015, x =9 : y = -4,3 x9 +617,05 ~578.
Partie B.
En 2013, dans le lycée de cette commune, on a compté 240 élèves absents
pour raison médicale parmi lesquels il y a 108 filles.
On sait que 25% de ces filles ont été absentes à cause de la grippe et
que 12,5 % des élèves absents pou raison médicale sont des garçons
atteints de la grippe.
1. On a commencé à
remplir un tableau résumant la situation décrite et dans lequel figure
une donnée dans la case grisée.
|
Nombres
d'élèves absents
à cause de la grippe
|
Nombre
d'élèves absents
pour une raison médicale
autre que la grippe
|
Total
|
Nombre
de filles absentes
pour raison médicale
|
108
x0,25=27
|
108-27=81
|
108
|
Nombre
de garçons absents
pour raison médicale |
30
|
132-30=102
|
132
|
Total
|
57
|
183
|
240
|
a. Décrire par une
phrase ce que signifie le nombre « 30 » indiqué dans cette case grisée.
30 garçons sont absents à cause de la grippe.
b. Indiquer le
calcul effectué pour obtenir ce nombre à partir des données de
l’exercice.
Nombre de garçons absents à cause de la grippe : 240 x0,125 =30.
c. Compléter le
tableau.
On choisit au hasard un élève absent pour raison médicale. On considère
les événements suivants :
F : « l’élève choisi est une fille » ;
M : « l’élève choisi a été absent à cause de la grippe ».
2. Calculer la
probabilité de l’événement F, notée p(F).
p(F) = nombre de filles / nombre d'élèves = 108 / 240 =0,45.
3. a. Décrire par
une phrase l’événement F ∩M.
Une fille a été absente à cause de la grippe.
b. Calculer la
probabilité de l’événement F ∩M , notée p(F ∩M).
Nombre de filles malades à cause de la grippe / nombre d'absents = 27 /
240 = 0,1125.
4. Montrer que la
probabilité de choisir un élève absent à cause de la grippe est 0,2375.
57 élèves absents pour cause de grippe sur 240 absents = 57 /
240=0,2375.
5. Calculer la
probabilité de choisir une fille sachant que l’absence est due à la
grippe.
27 filles grippés sur 57 grippés = 27 /
57= 9 / 19 ~0,474.
|
|
|
Antilles
Un magasin d’informatique propose différents
produits tels que des ordinateurs, du matériel d’impression ou des
logiciels.
Partie A.
80 clients ont acheté dans ce magasin un seul produit parmi ceux
proposés ci-dessus. Ils ont réglé soit en espèces soit en utilisant une
carte bancaire. Parmi ces clients :
• 70% ont payé en utilisant une carte bancaire, les autres ayant payé
en espèces ;
• 48 clients ont acheté du matériel d’impression;
• aucun ordinateur n’a été payé en espèces ;
• le quart de ceux qui ont payé en utilisant une carte bancaire a
acheté un logiciel ;
• parmi les clients ayant payé en espèces, il y en a autant qui ont
acheté un logiciel que du matériel d’impression.
1. Recopier et
compléter le tableau des effectifs ci-dessous, représentant la
répartition des achats et des modes de paiement des 80 clients
|
Matériel
d'impression
|
Logiciels
|
Ordinateurs
|
Total
|
Espèces
|
12
|
12
|
0
|
80-56=24
|
Carte
bancaire
|
36
|
14
|
6
|
80
x0,7=56
|
Total
|
48
|
26
|
6
|
80
|
2.
On choisit au hasard un des 80 clients. Chaque client a la même
probabilité d’être choisi.
On considère les évènements suivants :
A : « le client a acheté du matériel d’impression »
B : « le client a payé par carte bancaire ».
a. Calculer la
probabilité de l’évènement A.
48 clients sur 80 soit 48 / 80 = 0,60.
b. Calculer la
probabilité de l’évènement B.
56 clients sur 80 soit 56 / 80 = 0,70
c. Décrire par une
phrase l’évènement A∩B.
Le client a acheté du matériel d'impression et a payé par carte
bancaire.
d. Calculer la
probabilité de l’évènement A∩B.
36 / 80 = 0,45.
e. Décrire par une
phrase l’évènement suivant et.calculer sa probabilité.
Probabilité de "client a acheté du matériel d'impression ou a payé par
carte bancaire" :
p(A) +p(B) -p(A∩B)=0,60
+ 0,70 -0,45 = 0,85..
3. Sachant qu’un
client a acheté du matériel d’impression, calculer la probabilité qu’il
ait payé en espèces.
12 / 48 = 0,25.
Partie B
1. Soit f la
fonction définie sur l’ intervalle [1 ; 10] : f (x) = x2−12x
+96
a. On note f '(x)
la fonction dérivée de la fonction f . Calculer f '(x) pour tout x
appartenant à l’intervalle [1 ; 10].
f '(x)=2x-12 = 2(x-6).
b. Étudier le signe
de f '(x) pour x appartenant à l’intervalle [1 ; 10].
Si x appartient à [1 ; 6[, f '(x) est négative ; f(x) est décroissante.
Si
x appartient à ]6 ; 10], f '(x) est positive ; f(x) est strictement
croissante.
Si x = 6, f '(x) est nulle ; f(x) présente un minimum.
c. En déduire le tableau de
variation de la fonction f sur l’intervalle [1 ; 10].
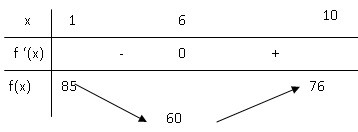
2. Le magasin
d’informatique se fournit en ordinateurs auprès d’une entreprise locale
qui peut fabriquer au maximum10 ordinateurs par semaine. On note x le
nombre d’ordinateurs produits en une semaine.
On admet que, pour tout x entier appartenant à l’intervalle [1 ; 10],
le coût total de fabrication, exprimé en dizaines d’euros, est égal à f
(x).
a. Déterminer le
nombre d’ordinateurs fabriqués par semaine qui permet un coût total de
fabrication minimal.
b. Donner la valeur
de ce coût minimal.
L'entreprise
fabrique 6 ordinateurs pour un coût minimal de 600 €.
|
|
|
|
Métropole septembre.
Le
tableau ci-dessous, extrait d’une feuille de calcul, donne le nombre de
licences sportives délivrées chaque année dans une ville :
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
1
|
Année
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
2
|
Rang
de l'année xi |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
3
|
Nombre
de licences yi
|
7093
|
7117
|
7331
|
7415
|
7587
|
7630
|
7820
|
7813
|
8090
|
4
|
Pourcentage
d'évolution ( en %)
|
|
|
|
|
|
|
|
|
|
Partie A.
1. Construire le
nuage de points de coordonnées xi, yi.
2. a. Calculer les
coordonnées du point moyen G de ce nuage de points.
b. Placer le point
moyen G sur le graphique.
xG = (1 +2 +3 +4 +5 +6 +7 +8 +9) / 9 =5.
yG = (7093 +7117 +7331 +7415 +7587 +7630 +7820 +7813 +8090)
/ 9 = 7544.
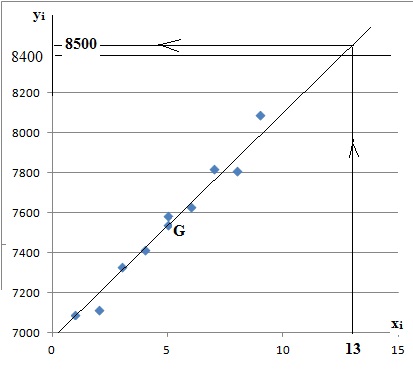
3. On considère la
droite (D), d’équation y = 121,15x+6938,25. On suppose que la droite
(D) réalise un ajustement affine du nuage de points, fiable jusqu’en
2017.
a. Montrer que le
point moyen G appartient à la droite (D).
121,15 x5 +6938,25=7544 = yG.
Les coordonnées du point G vérifient l'équation
de (D) : G appartient à cette droite.
b. Construire cette
droite sur le graphique précédent.
c. En utilisant la
représentation graphique, estimer le nombre de licences sportives qui
seront délivrées en 2017.
d. Retrouver par le
calcul l’estimation obtenue à la question précédente.
Rang de l'année 2017 : x = 13 ; y = 121,15 x13 +6938,25=8513.
Partie B.
On arrondira les pourcentages au dixième.
1. a. Déterminer le
pourcentage d’évolution du nombre de licences entre 2005 et 2006.
(7117-7093) / 7093 x 100 = 0,338 ~0,4 %.
b. Proposer une
formule, à saisir dans la cellule C4, qui, recopiée vers la droite,
permet de calculer le pourcentage d’évolution entre deux années
successives. Les résultats dans les cellules C4 à J4 sont au format
pourcentage.
=(C3-B3)/B3
2. Sachant qu’en
2013, 687 licenciés pratiquaient l’équitation, déterminer le
pourcentage qu’ils représentaient parmi l’ensemble des licenciés de
2013.
687 / 8090 x 100~8,5 %
3. Sachant que les
footballeurs représentaient 30% de l’ensemble des licenciés en 2013,
calculer le nombre de footballeurs licenciés en 2013.
8090 x0,3 =2427.
Lors d’une compétition, les 198 cyclistes participants ont été
contrôlés. Parmi eux, 21 cyclistes ont eu un résultat « positif » au
test anti-dopage.
Néanmoins, 3 cyclistes parmi ces 21 testés « positif » n’avaient pris
aucun produit dopant et 2 cyclistes parmi les testés « négatif »
avaient pris des produits dopants.
1. Compléter le
tableau suivant :
|
Cyclistes
dopés
|
Cyclistes
non dopés
|
Total
|
Cyclistes
testés positif
|
18
|
3
|
21
|
Cyclistes
testés négatif
|
2
|
175
|
177
|
Total
|
20
|
178
|
198
|
2. On choisit un
cycliste au hasard parmi les 198 compétiteurs. On considère les
évènements suivants :
D : « Le cycliste s’est dopé ».
N : « Le cycliste est testé "négatif" ».
a. Quelle est la
probabilité qu’un cycliste soit testé "positif" ?
p(D)=21 198 =0,106 ~0,11.
b. Calculer les
probabilités suivantes.
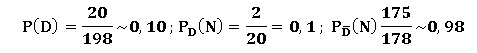
c. Exprimer par une
phrase l’évènement suivant puis calculer sa probabilité.

3. Compléter
l’arbre pondéré .
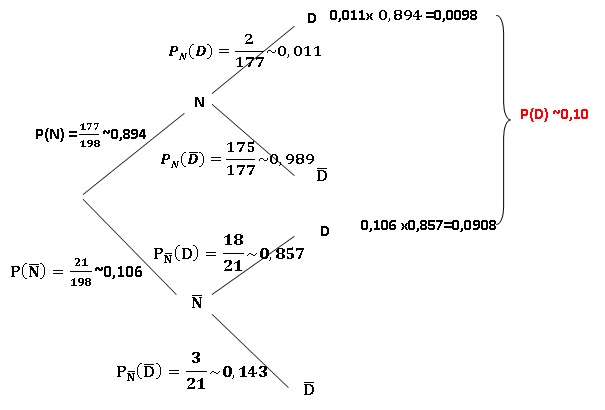
4. Déterminer
l’efficacité du test pratiqué lors de cette compétition.
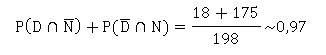
|
|
Antilles septembre.
L’indice de masse corporelle d’une personne (IMC) se calcule grâce à la
formule suivante : IMC = Masse / (Taille)2 dans laquelle
lamasse est exprimée en kilogramme et la taille en mètre.
On précise qu’une personne est en surpoids si son IMC est supérieur ou
égal à 25.
On a demandé à un groupe de 10 élèves de donner leur masse et leur
taille. Les données ont ensuite été consignées dans une feuille
automatisée de calcul reproduite ci-dessous :
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
1
|
Elève
n°
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
2
|
Masse
( kg)
|
54
|
65
|
64
|
70
|
72
|
61
|
64
|
76
|
45
|
78
|
3
|
Taille
(m)
|
1,73
|
1,84
|
1,65
|
1,62
|
1,70
|
1,74
|
1,86
|
1,57
|
1,60
|
1,71
|
4
|
IMC
|
18,0
|
19,2
|
23,5
|
26,7
|
24,9
|
20,1
|
18,5
|
30,8
|
17,6
|
26,7
|
La ligne 4 est au format nombre
avec une décimale.
1. Quelle formule a
été saisie dans la cellule B4 puis recopiée vers la droite jusqu’à la
cellule K4 pour calculer l’IMC des 10 élèves ?
=B2/(B3*B3)
2. Quelle est la
proportion d’élèves en surpoids dans ce groupe ? On exprimera le
résultat en pourcentage.
3 élèves sur 10 sont en surpoids soit 3 *100 / 10 = 30 %.
En 2012, en France, on
comptait une proportion d’hommes d’environ 47,5%.
Environ 42% des femmes et 54% des hommes étaient en surpoids. (source :
rapport OBEPI 2012)
On choisit une personne au hasard dans la population française, chaque
personne ayant la même probabilité d’être choisie.
On désigne par les lettres F, H et S les évènements suivants :
F : « la personne choisie est une femme »
H : « la personne choisie est un homme »
S : « la personne choisie est en surpoids »
1. a. Donner la
probabilité que la personne choisie soit une femme. On note P(F) cette
probabilité.
p(F) = 1-0,475 = 0,525.
b. Donner la
probabilité que la personne choisie soit en surpoids sachant que c’est
un homme.On note PH (S) cette probabilité.
PH (S)=0,54.
2.
Compléter l’arbre des probabilités donné dans l’annexe, à rendre avec
la copie.
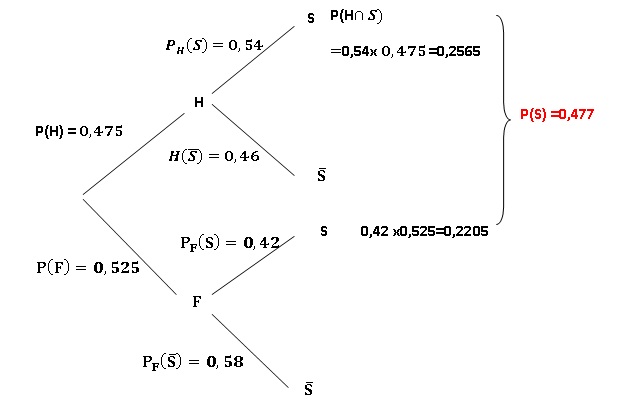
a. Décrire par une
phrase l’événement suivant H ∩S. et calculer sa probabilité.
La personne est un homme en surpoids.P(H ∩S) = 0,2565
~0,26.
3. Montrer que :
P(S)= 0,477.
4. Les évènements S
et H sont-ils indépendants ? Justifier la réponse.
P(H) x P(S) = 0,475 x 0,477 = 0,2266, valeur différente de P(H ∩S). Les
évenements S et H ne sont pas indépendants.
5. Calculer la
probabilité de choisir un homme sachant que la personne choisie est en
surpoids. On donnera le résultat arrondi à 0,001 près.
PS(H) = P(H ∩S) / P(S)
=0,2565 / 0,477 ~0,538.
Le tableau ci-dessous donne la population française, hors Mayotte, de
l’année 2004 à l’année 2013.
Année
|
Rang
de l'année ( xi)
|
Population
( yi) en milliers
|
2004
|
1
|
62251
|
2005
|
2
|
62731
|
2006
|
3
|
63186
|
2007
|
4
|
63601
|
2008
|
5
|
63962
|
2009
|
6
|
64305
|
2010
|
7
|
64613
|
2011
|
8
|
64949
|
2012
|
9
|
65281
|
2013
|
10
|
65586
|
Source : INSEE (en 2011, 2012
et 2013, les données sont provisoires)
On donne, en annexe, le nuage de points Mi (xi ; yi
).
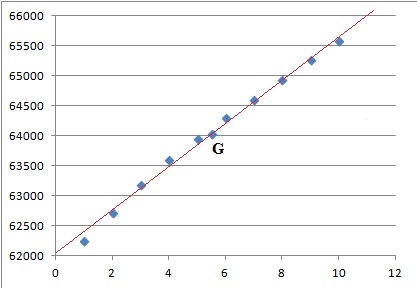
1. a. Montrer que
les coordonnées du point moyen G du nuage de points sont (5,5 ;
64 046,5), puis placer G sur le graphique.
xi =(1+2+3+4 +5+6+7 +8+9+10) /10=5,5.
yi = (62251 +62731 +63186 +63601 +63962 +64305 +64613 +64949
+65281 +65586) / 10 =64046,5.
b. On admet que la
droite D de coefficient directeur 364 passant par le point G constitue
un ajustement du nuage de point .
Montrer que l’équation réduite de la droite D est : y = 364x +62044,5.
La droite d'équation y = 364 x+b passe par G( 5,5 ; 64046,5) : 64046,5
= 364 x5,5 +b, d'où b =62044,5.
c. Tracer la
droite D sur le graphique.
2. En utilisant
l’ajustement précédent, déterminer par le calcul, une estimation de la
population française hors Mayotte, en 2015.
x = 12 ; y = 364 x12 +62044,5 = 66412,6 en milliers d'habitants.
En quelle
année, selon l’ajustement de la question 1. b., la population
française, hors Mayotte, dépasserait-elle 67 000 milliers d’habitants ?
364x +62044,5 > 67000 ; 364 x > 67000-62044,5 ; 364 x
>4955,5 ; x > 4955,5 / 364 ; x >13,6. x = 14, année 2017.
Nlle Calédonie.
Le tableau suivant donne l’évolution du nombre d’interruptions
volontaires de grossesse (I.V.G.)médicamenteuses dans les villes des
départements d’outre-mer de 2005 à 2011.
Année
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
Rang
(xi)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Nombre
d'IVG médicamenteuse (yi)
|
543
|
952
|
1338
|
1642
|
1967
|
2467
|
2511
|
Source : DREES,Ministère des
affaires sociales et de la santé
1. Calculer le
taux d’évolution du nombre d’I.V.G.médicamenteuses entre 2010 et 2011.
Arrondir le résultat à 0,1%.
(2511-2467) / 2467 x100 =1,78 ~1,8 %.
2. Représenter sur
une feuille de papiermillimétré le nuage de points.
3. Déterminer les
coordonnées du point moyen G de ce nuage de points. On arrondira
l’ordonnée de G à l’entier.
xi =(1 +2 +3 +4 +5 +6 +7) / 7 =4.
yi=(543 +952 +1338 +1642 +1967 +2467 +2511) / 7 ~1631.
Dans toute la suite de l’exercice, on prendra pour coordonnées de G(4 ;
1 631).
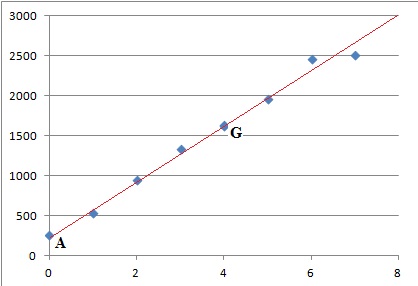
4. Soit le point
A(0 ; 265).
a. Tracer la
droite (AG) sur le graphique du nuage de points
b. Montrer que la
droite (AG) a pour équation : y = 341,5x +265.
La droite d'équation y = ax+b passe en A ; 265= 0 +b.
La droite passe en G : 1631 = 4a +265 d'où a = (1631-265) / 4 = 341,5.
5. On admet que la
droite (AG) est un ajustement affine pertinent du nuage de points qui
permet d’effectuer des estimations au-delà de 2011. En utilisant cet
ajustement affine, calculer :
a. le nombre
d’I.V.G.médicamenteuses dans les villes des départements d’outremer en
2014 ;
x = 10 ; y = 3415+265 = 3680.
b. l’année à partir
de laquelle le nombre d’I.V.G. médicamenteuses dans les villes des
départements d’outre-mer dépassera 4 500.
341,5x +265 > 4500 ;
341,5 x > 4235 ; x > 4235 / 341,5 ; x >12,4 ; x = 13, année
2017.
Chaque année on déplore des accidents de la route mortels (c’est-à-dire
ayant entraîné un décès au moins).
Le tableau ci-dessous indique le nombre de conducteurs de voiture de
tourisme impliqués dans un accident mortel en 2011, en fonction de leur
alcoolémie et du port
de la ceinture de sécurité.
|
Test
d'alcoolémie positif
|
Test
d'alcoolémie négatif
|
Total
|
Nombe
de conducteurs ceinturés
|
383
|
2185
|
2568
|
Nombre
de conducteurs non ceinturés
|
167
|
92
|
259
|
Total
|
550
|
2277
|
2827
|
Source : ONISR, Fichier des accidents
Dans les questions suivantes, les résultats seront donnés sous forme
décimale et arrondis au millième.
On prélève au hasard le dossier d’un conducteur parmi les 2 827
conducteurs impliqués dans des accidents mortels.
On considère les évènements suivants :
A : « Le test d’alcoolémie du conducteur était positif au moment de
l’accident » ;
C : « Le conducteur était ceinturé au moment de l’accident ».
1. Calculer la
probabilité que le test d’alcoolémie du conducteur ait été positif au
moment de l’accident.
P(A) =550 / 2827 ~0,195.
2. Calculer la
probabilité que le conducteur n’ait pas été ceinturé au moment de
l’accident.
259 / 2827 ~ 0,092.
3. a. Décrire par une phrase l’évènement suivant.et montrer que sa
probabilité est environ égale à 0,227.
Le conducteur n'était pas ceinturé ou bien le test d'alcoolémie
était positif.
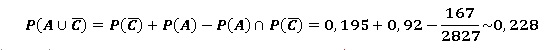
4. a. Quelle est la probabilité que le
conducteur n’ait pas été ceinturé, sachant que son test d’alcoolémie
était négatif ?
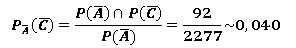
b. Calculer la
probabilité suivante.
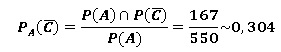
c. Comparer ces
deux derniers résultats et commenter par une phrase.
En buvant, on oublie de mettre la ceinture.
|
|