Fonction, suite,
probabilités, tétraèdre. Bac S Nlle Calédonie 03 /17.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
....
.....
|
Exercice1.
On considère la fonction f définie et dérivable sur [0 ; +∞[ par f (x)
= xe−x et on note Cf sa courbe représentative
dans un repère orthogonal.
Partie A.
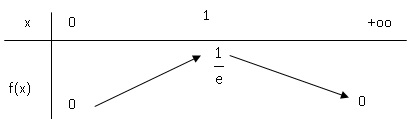
1. Justifier
toutes les informations du tableau de variations de f donné ci-dessous.
Quand x = 0, e-x =1 et f(x) = zéro.
Quand x tend vers plus l'infini, e-x tend
vers zéro et par croissance comparée x / ex tend vers zéro.
Dériver en posant : u = x
et v = e-x ; u' = 1 ; v' =-e-x ; f '(x) =u'v +v'u
= e-x-xe-x =e-x(1-x).
f '(x) s'annule pour x = 1.
e-x est positif ; f '(x) est positive pour x <1 et
négative pour x >1.
f(x) est strictement croissante sur [0 ; 1[ et strictement
décroissante sur ]1 ; +oo[.
f(1) = e-1.
2- Soit F la
fonction définie et dérivable sur [0 ; +∞[ par F(x) = (−x −1)e−x
.
Démontrer que la fonction F est une primitive de f sur [0 ; +∞[.
Dériver F en posant u = -x-1 et v = e-x ; u' = -1 ; v' = -e-x.
F '(x) = u'v +v'u= -e-x+(x+1)e-x =x e-x
= f(x).
Partie B.
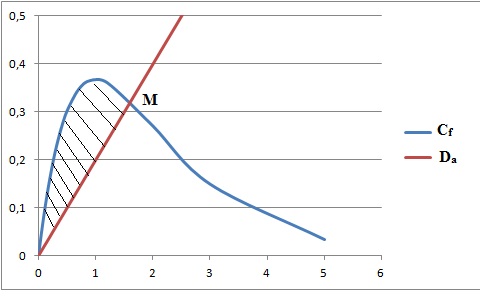
Soit a un nombre réel tel que 0 < a < 1. On considère la droite Da
d’équation y = ax et M le point d’intersection de la droite Da
avec la courbe Cf . On note xM l’abscisse du
point M.
On note H(a) l’aire, exprimée en unités d’aire, du domaine hachuré sur
le graphique ci-dessous, c’est-à-dire du domaine situé sous la courbe Cf
au-dessus de la droite Da et entre les droites d’équation x
= 0 et x = xM.
Le but de cette partie est d’établir l’existence et l’unicité de la
valeur de a telle que H(a)= 0,5 puis d’étudier un algorithme.
1. Prouver que la
droite Da et la courbe Cf ont un unique point
d’intersection M distinct de l’origine.
xe-x = ax ; x(e-x-a)=0 ; x=0 et x= -ln(a).
La droite et la courbe se coupent à l'origine et en M tel que xM
= -ln (a).
On admet dans la suite de l’exercice que le point M a pour abscisse xM
= −lna et que la courbe Cf est située au-dessus de la droite
Da sur l’intervalle [0 ; −ln(a)].
2. Montrer que
H(a)= a ln(a)−0,5a (ln(a))2+1-a
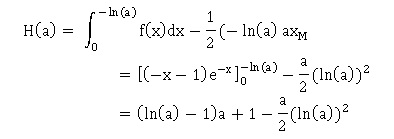
3. Soit la fonction
H définie sur ]0 ; 1] parH(x)= x ln(x)−0,5 x(ln(x))2+1−x.
On admet que H est dérivable sur ]0 ; 1] et que son tableau de
variations correspond à celui qui est proposé ci-dessous.
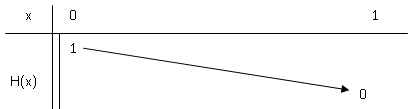
Justifier
qu’il existe un unique réel a
∈]0 ; 1[ tel que H(a)
= 0,5.
H(x) est continue et strictement décroissante ]0 ; 1] et diminue de 1 à
0 . D'après le théorème des valeurs intermédiaires, il existe un unique
réel a ∈]0 ; 1[ tel que H(a) = 0,5.
4. On considère
l’algorithme présenté ci-dessous.
VARIABLES : A, B et C sont des nombres ;
p est un entier naturel.
INITIALISATION : Demander la valeur de p
A prend la valeur 0
B prend la valeur 1
TRAITEMENT : Tant que B − A > 10−p
C prend la valeur (A+B)/2
Si H(C)> 0,5
Alors A prend la valeur de C
Sinon B prend la valeur de C
Fin de la boucle Si
Fin de la boucle Tant que
SORTIE : Afficher A et B.
Que représentent les valeurs A et B affichées en sortie de cet
algorithme ?
L'algorithme détermine un encadrement à 10-p de la solution
de H(x) = 0,5.
A est la borne inférieure et B la borne supérieure.
5. Donner un
encadrement d’amplitude 0,01 de a.

a est
compris entre 0,06 et 0,07.
|
| .
. |
|
|
Exercice 2. QCM
1. La durée de vie
T (exprimée en années) d’un appareil électronique suit la loi
exponentielle de paramètre l
positif.
On sait qu’un tel appareil a une durée de vie moyenne de quatre ans.
La probabilité que cet appareil fonctionne deux années de plus sachant
qu’il a déjà fonctionné trois ans est d’environ 0,39 à 0,01 près. Faux.
La loi exponentielle est sans mémoire ; P(X >2) = e-2l avec l = 1/4 = 0,25.
P(X>2) = e-0,5 ~0,61.
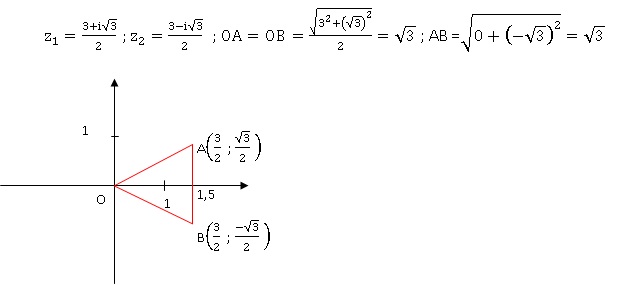
2. Le plan complexe
est muni d’un repère orthonormal.
L’équation z3−3z2+3z = 0 admet trois solutions
dans l’ensemble des nombres complexes C, qui sont les affixes de trois
points formant un triangle équilatéral. Vrai.
z(z2-3z+3)=0 ; première solution z = 0.
z2-3z+3=0
; discriminant D = (-3)2 -4x3 = -3 = 3 i2.
|
|
|
|
Exercice
3.
Des étudiants d’une université se préparent à passer un examen pour
lequel quatre thèmes (A, B, C et D) sont au programme.
Partie A.
Sur les 34 sujets de l’examen déjà posés, 22 portaient sur le thème A.
Peut-on rejeter au seuil de 95% l’affirmation suivante : « il y a une
chance sur deux que le thème A soit évalué le jour de l’examen » ?
Hypothèse
: il y a une chance sur 2 que le thème A soit évalué.
p = q = 0,5 ; n = 34 >
30.
np = nq = 34 x0,5 = 17 >5.
Les conditions sont vérifiées pour que l'on établisse un intervalle de
fluctuation asymptotique au seuil de 95 %.
1,96 (pq / n)½ = 1,96 (0,5 x0,5 / 34)½ ~0,168 ;
intervalle de fluctuation [0,5 -0,168 ; 0,5 +0,168 ] soit [ 0,33 ; 0,67
].
Fréquence du thème A : 22 / 34 ~0,65.
Cette valeur appartient à l'intervalle de fluctuation, l'hypothèse est
valide.
Partie B.
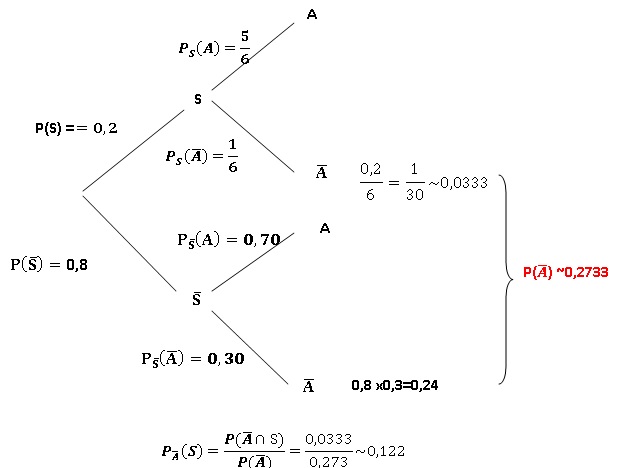
Le thème A reste pour beaucoup d’étudiants une partie du programme
difficile à maîtriser. Un stage de préparation est alors proposé pour
travailler ce thème. Lors de l’examen, on a constaté que s’il y a un
exercice portant sur le thème A :
• 30% des étudiants n’ayant pas sμivi le stage ne traitent pas
l’exercice ;
•5 / 6 des étudiants ayant suivi le stage l’ont traité.
On sait de plus que 20% des étudiants participent au stage.
Lors des résultats de l’examen, un étudiant s’exclame : « Je n’ai pas
du tout traité le thème A ».
Quelle est la probabilité que cet étudiant ait suivi le stage ? On
arrondira le résultat à 0,001 près.
Evénement S " l'étudiant a suivi le stage" ; événement A :" le
thème A est traité".
Partie C.
On suppose que la variable aléatoire T , associant la durée (exprimée
en minutes) que consacre un étudiant de cette université pour la
composition de cet examen, suit la loi normale d’espérance μ = 225 et
d’écart-type s
> 0.
La probabilité qu’un étudiant finisse son examen en moins de 235
minutes est de 0,98.
Déterminer une valeur approchée de s à 0,1 près.
On pourra, par exemple, introduire la variable aléatoire Z =(T−225) /s.
Z suit la loi normale centrée réduite ( moyenne zéro, écart type 1).
On cherche le nombre réel ß tel que P(Z< ß) = 0,98. Les tables
ou la calculatrice donne ß = 2,054.
s
=(235-225) /2,054 =4,869 ~4,9.
Exercice 5.
On considère la suite (un) définie par : u0 = 0 ;
un+1 =1 /(2-un) pour tout entier naturel n >0.
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Un
|
0
|
0,5
|
2/3
|
3/4
|
4/5
|
5/6
|
6/7
|
7/8
|
8/9
|
Prouver que la suite (un) converge.
Hypothèse : un = n / (n+1)
Démonstration par récurence :
Initialisation
: u1 =1/(2) = 0,5 est vérrifié.
Hérédité :
l'hypothèse est supposée vraie au rang p : up = p / (p+1).
up+1= 1 / [2-p /(p+1)] = 1 / [(p+2) / (p+1)]= (p+1) / (p+2).
L'hypothèse est vraie au rang p+1.
Conclusion
: l'hypothèse est vraie au rang 1 et héréditaire.
Donc un = n /( n+1) quel que soit n entier naturel.
un = 1
/( 1+1/n) ; 1 /n tend vers zéro quand n tend vers l'infini et un
tend vers 1.
|
|
|
|
Exercice 5.
L’espace est muni d’un repère orthonormé (O; i, j, k).
On considère les points A(−1 ; −1 ; 0), B(6 ; −5 ; 1), C(1 ; 2 ; −2) et
S(13 ; 37 ; 54).
1. a. Justifier que
les points A, B et C définissent bien un plan.

Les points A, B et C ne sont pas alignés : ils définissent un plan.
b. Prouver que le
vecteur de coordonnées (5 ; 16 ; 29) est un vecteur normal au plan
(ABC).
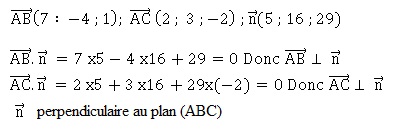
c. En déduire une
équation cartésienne du plan (ABC).
5x +16y +29 z = a.
A (-1 ; -1 ; 0) appartient au plan (ABC) :
5x(-1) +16x(-1) +29 x0 = a ; a = -21.
5x +16y +29 z + 21=0.
2. a. Déterminer la
nature du triangle ABC.
AB = [72 +(-4)2 +12]½=66½.
AC = [22 +32 +(-2)2]½=17½.
BC =[(-5)2 +72 +(-3)2]½=83½.
BC2 = AC2 +AB2, le triangle ABC est
rectangle en A, d'après la réciproque du théorème de Pythagore.
b. Démontrer que la
valeur exacte de l’aire du triangle ABC est, en unités d’aire : 0,5
x(1122)½.
AB xAC / 2 = (66x17)½/2 = 1122½ /2.
3. a. Prouver que
les points A, B, C et S ne sont pas coplanaires.
Ces quatres points sont coplanaires si S(13 ; 37 ; 54) appartient au
plan ( ABC) d'équation 5x +16y +29 z + 21=0.
5x13 +16 x37 +29x54 +21 différe de zéro, donc S n'appartient pas au
plan ( ABC).
b. La droite (D) perpendiculaire au plan
(ABC) passant par le point S coupe le plan (ABC) en un point noté H.
Déterminer les coordonnées du point H.
Equation paramétrique de la droite (D), perpendiculaire au plan
( ABC) :
x = 5t+xS = 5t +13 ; y =16t +yS = 16t+37 ; z =
29t +zS = 29t +54.
H appartient au plan ( ABC) : 5 xH +16yH +29zH
+21 = 0.
H appartient à la droite (D)
: xH = 5t +13 ; yH = 16t+37 ; zH
= 29t +54.
25 t+5*13+16*16t+16*37+29*29t+29*54+21=0 ; 1122 t +2244=0 d'où t
= -2.
xH = 5x(-2) +13 = 3 ; yH = 16x(-2)+37= 5 ; zH
= 29x(-2) +54= -4.
4. Déterminer le
volume du tétraèdre SABC.
Hauteur SH =[(3-13)2 +(5-37)2+(-4-54)2]½
=4488½ ~67.
Aire de base : 1122½ /2.
Volume du tétraèdre : hauteur x aire de base / 3 = (4488 x1122)½
/ 6 = 2244 / 6=374 unités de volume.
|
|