Mathématiques,
géométrie dans l'espace, Bac S 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry.
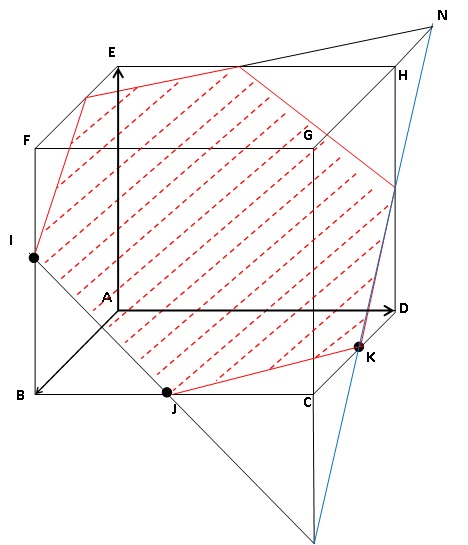
ABCDEFGH
désigne un cube de côté 1. Le point I est le milieu du segment [BF]. Le
point J est le milieu du segment [BC]. Le point K est le milieu du
segment [CD].
Partie
A.
Dans cette partie, on ne demande aucune justification
On admet que les droites (IJ) et (CG) sont sécantes en un point L.
Construire, sur la figure et en laissant apparents les traits de
construction:
• le point L ;
• l’intersection D des plans (IJK) et (CDH) ;
• la section du cube par le plan (IJK).
Partie
B.
1. Donner les
coordonnées de A, G, I, J et K dans ce repère ci-dessus.
A(0 ; 0 ; 0 ) ; G( 1 ; 1 ; 1 ) ; I( 1 ; 0 ; ½ ) ; J( 1 ; ½ ; 0 ) ; K( ½
; 1 ; 0 ).
2. a. Montrer que
le vecteur AG est normal au plan (IJK).

b. En déduire une
équation cartésienne du plan (IJK).
Soit un point P(x ; y ; z ) du plan (IJK).
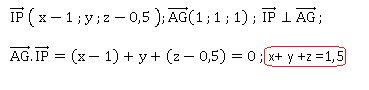
3. On désigne par M
un point du segment [AG] et t le réel de l’intervalle [0 ; 1] tel que 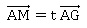
a. Démontrer que MI2
= 3t 2 −3t +1,25.
Coordonnées du point M : M(t ; t ; t )
Coordonnées du vecteur MI : 1-t ; -t ; 0,5-t.
MI2 = (1-t)2 + (-t)2 + (0,5-t)2
= 1+t2-2t+t2+0,25+t2-t =3t2-3t+1,25.
b. Démontrer que la
distance MI est minimale pour le point Mmini(0,5 ; 0,5 ;
0,5).
Le trinome ax2 +bx+c est minimal pour x = -b /(2a) ; MI2
et donc MI, est minimal pour t = 3/6 =0,5.
Coordonnée du point Mmini correspondant à t = 0,5 :Mmini
( 0,5 ; 0,5 ; 0,5 ).
4. Démontrer que
pour ce point (0,5 ; 0,5 ; 0,5) :
a. N appartient au
plan (IJK).
Equation du plan (IJK) : x +y +z = 1,5.
xMmini + y Mmini + zMmini = 0,5 +0,5
+0,5 = 1,5 : Mmini appartient au plan (IJK).
b. La droite (IMmini)
est perpendiculaire aux droites (AG) et (BF).
Les points I et Mmini appartiennent au plan ( IJK) et le
vecteur AG est normal à ce plan.
On en conclut que les droites (IMmini) et (AG) sont
orthogonales.
Or le point Mmini est le milieu de [AG]
On
en conclut que les droites (IMmini) et (AG) sont
orthogonales en Mmini.
|
| .
. |
|
|
Liban.
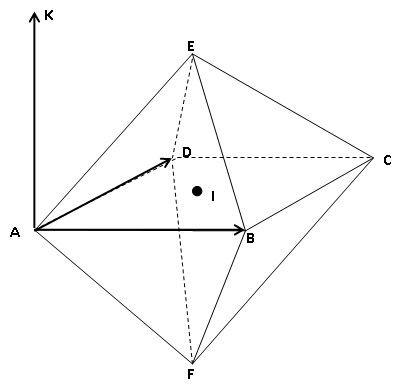
On
considère un solide ADECBF constitué de deux pyramides identiques ayant
pour base commune le carré ABCD de centre I.Toutes les arêtes sont de
longueur 1.
L’espace est rapporté au repère orthonormé ci-dessous.
1. a. Montrer que
IE =2½ / 2.
. En déduire les coordonnées des points I, E et F.
Les deux pyramides sont identiques, régulières, à base carrée, et leurs
arètes ont la même longueur, l'unité. E et F ont pour projeté
orthogonal, le centre I du carré ABCD.
Donc AC = 2½ et AI = ½AC = 2½/2.
Le triangle AEI est rectangle en I : IE2 = AE2-AI2
= 1-(2½/2)2=0,5
; IE =2½/2.
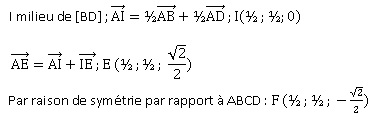
b. Montrer que le vecteur n de
coordonées (0 ; -2 ; 2½ ) est normal au plan (ABE).
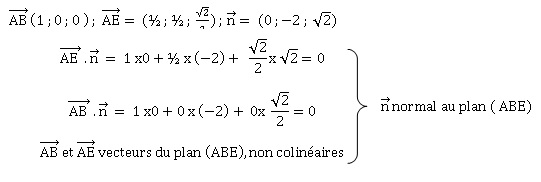
c. Déterminer une
équation cartésienne du plan (ABE).
Soit un point P(x ; y ; z ) du plan (ABE).
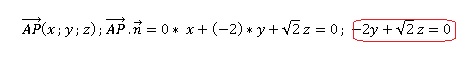
2. On nomme M le milieu du segment
[DF] et N celui du segment [AB].
a. Démontrer que
les plans (FDC) et (ABE) sont parallèles.
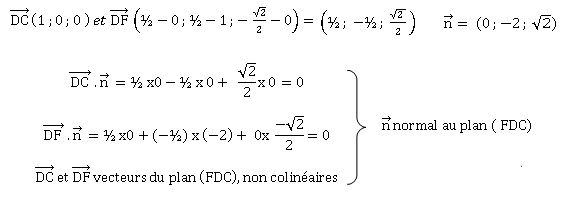
Les plans ( FDC) et (ABE) sont normaux au même vecteur, ils sont donc
parallèles.
b. Déterminer
l’intersection des plans (EMN) et (FDC).
Le point M appartient au segment [EM] et M est le milieu du
segment [FD] : M appartient à l'intersection des plans (FDC) et EMN).
Les plans (FDC) et (ABC) étant parallèles, le plan ( EMN) les coupe
suivant deux droites parallèles.
La droite (EN) étant l'intersection des plans (EMN) et (ABE), la droite
parralèle à (EN) passant par M est l'intersection cherchée.
c. Construire
la section du solide ADECBF par le plan (EMN).
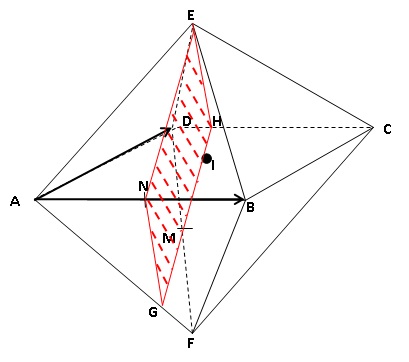
[MH] intersection du plan (EMN) avec la fgace (FCD)
[NG] intersection du plan (EMN) par la face (ABF).
[EN] intersection du plan (EMN) par la face (ABE).
|
|
Antilles Guyanne.
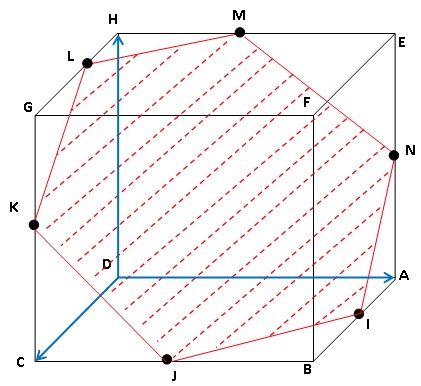
ABCDEFGH est un cube d’arête égale à
1.
L’espace est muni du repère orthonormé desiné en bleu.
Dans ce repère, on a : D(0 ; 0 ; 0), C(1 ; 0 ; 0), A(0 ; 1 ; 0), H(0 ;
0 ; 1) et E(0 ; 1 ; 1).
Soit I le milieu de [AB].
Soit P le plan parallèle au plan (BGE) et passant par le point I .
On admet que la section du cube par le plan P représentée ci-dessus est
un hexagone dont les sommets I , J , K, L, M, et N appartiennent
respectivement aux arêtes
[AB], [BC], [CG], [GH], [HE] et [AE].
1. a. Montrer que
le vecteur DF est normal au plan (BGE).
On démontre que ce vecteur est orthogonal à deux vecteurs non
colinéaires du plan ( BGE).
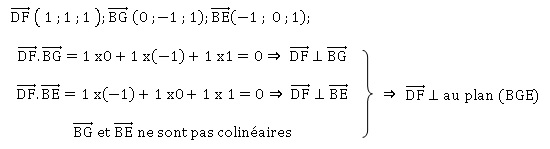
b. En déduire une
équation cartésienne du plan P.
Soit
un point Q(x ; y ; z ) du plan P; I appartient également au plan P.
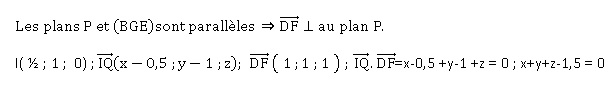
2. Montrer que le point N est le
milieu du segment [AE].
Les intersections de deux plans parallèles, P et (BGE), avec la plan
(ABE) sont deux droites parallèles. Ces droites sontt (IN) et (BE).
Théorème de Thalès dans les triangles ABE et AIN : AI / AB = 0,5 = AN /
AE. N est donc le milieu du segment [AE].
3. a. Déterminer
une représentation paramétrique de la droite (HB).
Cette droite (HB) passe par le point H(0 ; 0 ; 1) et par le point B(1 ;
1 ; 0).

b. En déduire que
la droite (HB) et le plan P son sécants en un point T dont on précisera
les coordonnées.
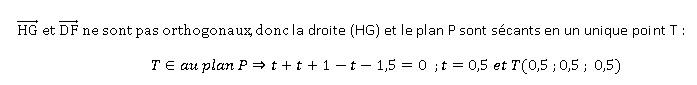
4. Calculer, en
unités de volume, le volume du tétraèdre FBGE.
La base de ce tétraèdre est le triangle rectangle FBG d'aire
B=½FG x BF = 0,5 unité d'aire.
Hauteur du tétraèdre FE = 1.
Volume du tétraèdre V = B x FE / 3 = 0,5 x1 /3 = 1 / 6 unité
d'aire.
Nlle
Calédonie.
On considère le cube ABCDEFGH représenté ci-dessous.
1. Tracer, sans
justifier, la section du cube par le plan (IJK) où K est un point du
segment [BF].
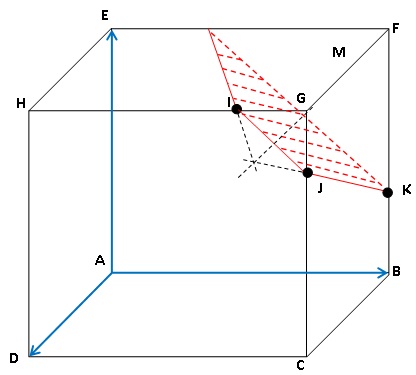
2. Tracer, sans justifier, la section du cube
par le plan (IJL) où L est un point de la droite (BF).
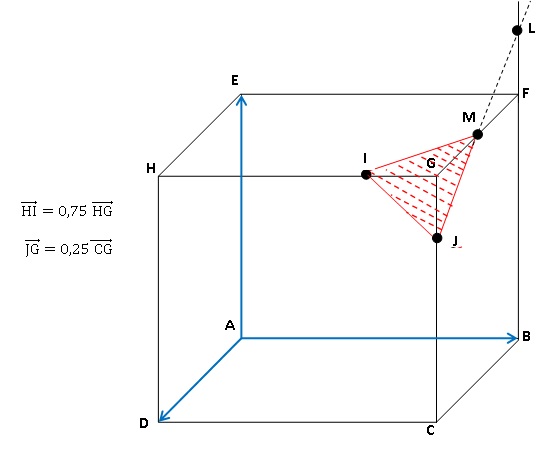
3. Existe-t-il un
point P de la droite (BF) tel que la section du cube par le plan (IJP)
soit un triangle équilatéral ? Justifier votre réponse.
On note K un point du segment [GF] tel que GK = 0,25 GF.
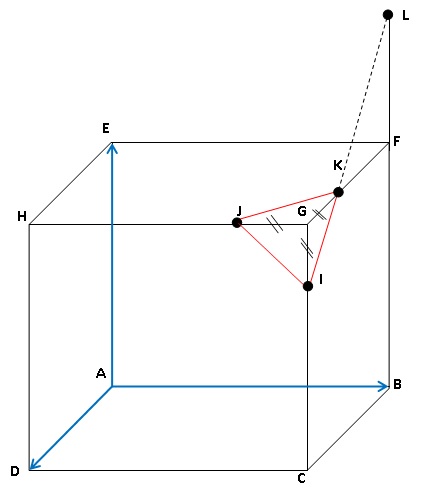
Les trois triangles IJG, IGK et JGK sont superposables.Donc JK=IJ =IK
et le triangle IJK est équilatéral.
Ecrire le théorème de Thalès dans les ttriangles IGK et LFK en
remarquant que KF = 3 GK.
FL / IG = KF / GK = 3 ; FL = 3 IG.
Le point L est tel que FL est égal au 3 / 4 du côté du cube.
Amérique
du sud.
Partie A : un
calcul de volume sans repère
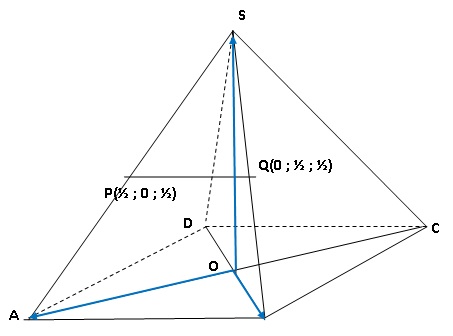
On considère une pyramide équilatère SABCD (pyramide à base carrée dont
toutes les faces latérales sont des
triangles équilatéraux).Les diagonales du carré ABCD mesurent 24 cm. On
note O le centre du carré ABCD.
On admettra que OS = OA.
1. Sans utiliser de
repère, démontrer que la droite (SO) est orthogonale au plan (ABC).
Le triangle SAC est isocèle car SA = SC.
O étant le milieu du segment [AC], OS est la médiane issue de S dans le
triangle SAC.
Ce triangle étant isocèle en S, la médiane issue de S est également
médiatrice du côté AC.
En conséquence (SO) et (AC) sont perpendiculaires.
Une démonstration identique dans le triangle SBd conduit à : (SO)
et (BD) sont perpendiculaires.
Les deux droites sécantes (BD) et (AC) du plan ( ABC) sont
perpendiculaires à la droite ( OS).
La droite (OS) est donc orthogonale au plan ( ABC).
2.
En déduire le volume, en cm3, de la pyramide SABCD.
Aire de la base carré ABCD : A
= AB2 avec 2AB2 = AC2
=242 =576 ; AB2 =288
cm2.
Volume de la pyramide : V =
A
x OS / 3 = 288 x 12 / 3 = 1152 cm3.
Partie B : dans un
repère
On considère le repère orthonormé représenté en bleu.
1. On note P et Q
les milieux respectifs des segments [AS] et [BS].
a. Justifier que le
vecteur n de coordonnées (1 ; 1 ; −3) est un vecteur normal au plan
(PQC).
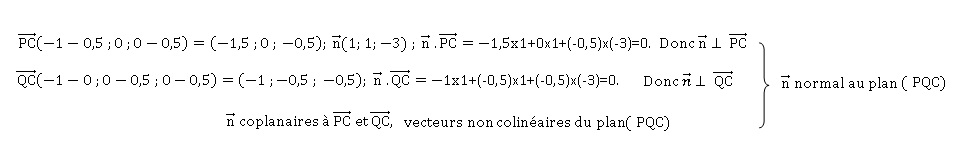
b. En déduire une
équation cartésienne du plan (PQC).
Soit M( x ; y ; z) un point du plan ( PQC).
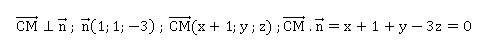
Equation du plan (PQC) : x +y -3z+1=0.
2. Soit H le point
du plan (PQC) tel que la droite (SH) est orthogonale au plan (PQC).
a. Donner une
représentation paramétrique de la droite (SH).
La droite (SH) est orthogonale au plan (PQC) ; le vecteur 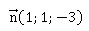 est orthogonal au plan ( PQC). est orthogonal au plan ( PQC).
Donc le vecteur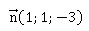 est un vecteur directeur de la droite (SH).
est un vecteur directeur de la droite (SH).
Le point S(0 ; 0 ; 1) appartient à cette droite (SH).
Représentation paramétrique de cette droite (SH) : k appartenant à R.
x= k ; y = k ; z =1-3k.
b. Calculer les
coordonnées du point H.
Le point H est l'intersection de la droite (SH) et du plan (PQC) ; les
coordonnées du point H sont telles que :
x+y-3z+1 = 0 ; k+k-3+9k+1=0 ; 11 k = 2 ; k = 2 /11.
H ( 2/11 ; 2 /11 ; 1-6/11) soit H(2/11 ; 2/11 ; 5/11).
c. Montrer alors
que la longueur SH, en unité de longueur, est 2 x 11-½.
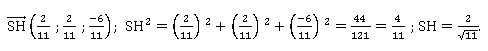
3. On admettra que
l’aire du quadrilatère PQCD, en unité d’aire, est égale à 3 x11½/8.
Calculer le volume de la pyramide SPQCD, en unité de volume.
Volume =Aire du quadrilatère de base PQCD fois hauteur SH / 3.
V = 3 x11½/8 x 2
x 11-½ / 3 = 0,25 unité de volume.
Partie C
: partage équitable
Pour l’anniversaire de ses deux jumelles Anne et Fanny, Madame Nova a
confectionné un joli gâteau en forme de pyramide équilatère dont les
diagonales du
carré de base mesurent 24 cm. Elle s’apprête à le partager en deux,
équitablement, en plaçant son couteau sur le sommet. C’est alors
qu’Anne arrête son geste et lui propose une découpe
plus originale : « Place la lame sur le milieu d’une arête,
parallèlement à un côté de la base, puis coupe en te dirigeant vers le
côté opposé ».
Fanny a des doutes, les parts ne lui semblent pas équitables. Est-ce le
cas ? Justifier la réponse.
OA correspond à une unité de longueur soit 12 cm. L’unité de volume
vaut 123 = 1728 cm3.
Volume de la pyramide SABCD : 1 152 cm3.
Le volume de la pyramide SPQCD = 0,25 unité de volume = 0,25×1728 = 432
cm3, valeur différente de 1152 / 2 = 576 cm3.
Le partage proposé par Fanny n’est pas équitable.
|
|