Mathématiques,
nombre complexes, bac S 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie
Le plan complexe
est rapporté à un repère orthonormé
. À tout point M d’affixe z du plan, on associe le point M′ d’affixe z′
définie par :
z′ = z2 +4z +3.
1. Un point M est
dit invariant lorsqu’il est confondu avec le point M′ associé.
Démontrer qu’il existe deux points invariants. Donner l’affixe de
chacun de ces points sous forme algébrique, puis sous forme
exponentielle.
z=z2 +4z +3 ; z2
+3z +3=0.
Discriminant D = b2-4ac=32-4x3=-3
=3i2.
Cette équation admet deux solutions.
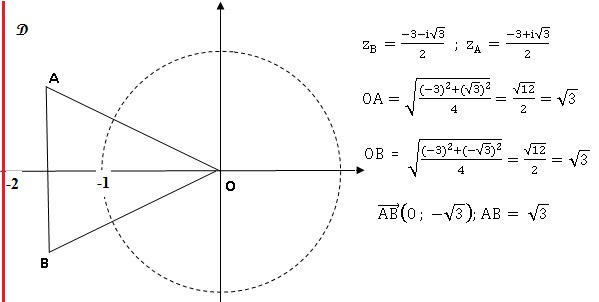
2. Montrer que OAB est un triangle
équilatéral.
3. Déterminer
l’ensemble E des points M d’affixe z = x+iy où x et y
sont réels, tels que le point M′ associé soit sur l’axe des réels.
z'= x ; z' =z2 +4z
+3 ;
x = (x+iy)2 +4(x+iy)+3 ; x = x2-y2+2ixy+4x
+4iy +3.
Par identification : x2-y2+3x+3=0 et
2xy+4y=0.
2y(x+2)=0 soit y=0 et x= -2.
4. Dans
le plan complexe, représenter les points A et B ainsi que
l’ensemble E .
.y=0 est l'axe des abscisses et x=-2 est
l'équation de la droite D.
Antilles.
Dans
le plan complexemuni d’un repère orthonormé on a placé un point M
d’affixe z appartenant à C, puis le point R intersection du cercle de
centre O passant par M et de l'axe des abscisses.
1. Exprimer
l’affixe du point R en fonction de z.
OR = OM d'où zR = |z|.
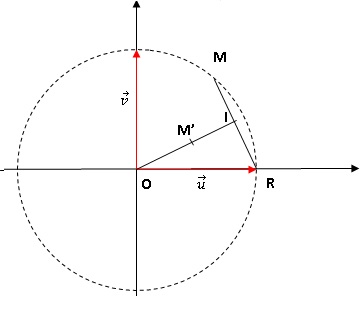
2. Soit le point M′
d’affixe z′ définie par z′ =0,5(z +|z| )/2.
Reproduire la figure sur la copie et construire le point M′.
Le point d'affixe (z +|z| )/2 est le milieu I du segment
[MR].
Le point d'affixe z' est la milieu M' du segment [OI].
On définit
la suite de nombres complexes (zn) par un premier terme z0
appartenant à C et, pour tout entier naturel n, par la relation de
récurrence :
zn+1 =(zn +|zn| )/4.
Le but de cette partie est d’étudier si le comportement à l’infini de
la suite (|zn|) dépend du choix de z0.
1. Que peut-on dire
du comportement à l’infini de la suite (|zn|) quand z0
est un nombre réel négatif ?
|z0|= -z0 ; z1=(z0
-z0 )/4 =0.
Tous les termes suivants de la suite sont nuls. La suite converge vers
zéro.
2. Que peut-on dire du comportement
à l’infini de la suite (|zn|) quand z0 est un
nombre réel positif ?
|z0|= +z0
; z1=(z0 +z0 )/4 =z0/2.
z2=(z1
+|z1| )/4 =z0/4.
Montrons par récurrence que zn = z0/(2n).
Initialisation
: z1=z0/2.
Hérédité :
on suppose que zp = z0/(2p).
zp+1 =(zp+|zp|)/4= [ z0 / (2p)+ z0 / (2p)]/4= z0 /(2 x2p)=z0 / (2p+1) .
La propriété est vraie pour p+1.
Conclusion :
la propriété est vraie au rang 1 et héréditaire. zn
= z0/(2n).
Il s'agit d'une suite géométrique de raison 0,5 ; elle converge vers
zéro.
3.
On suppose désormais que z0 n’est pas un nombre réel.
a. Quelle
conjecture peut-on faire sur le comportement à l’infini de la suite (|zn|)
?
La construction indique que le module de z' est égal à la moitié de
celui de z. On conjecture que la suite
(|zn|) converge vers zéro.
b. Démontrer cette conjecture, puis
conclure.
Pour tout nombre complexe z1 et z2 :

La
suite géométrique z0/(2n) converge vers
zéro. D'après le théorème des gendarmes, la suite (|zn|)
converge vers zéro.
|
| .
. |
|
|
Amérique du nord.
On se place dans un repère orthonormé et, pour tout
entier naturel n, on définit les
points (An) par leurs coordonnées ( xn ; yn
) de la façon suivante :
x0 = −3 ; y0 = 4
et pour tout entier naturel n :
xn+1 = 0,8xn −0,6yn ; yn+1
= 0,6xn +0,8yn
1. a. Déterminer
les coordonnées des points A0, A1 et A2.
A0 ( -3 ; 4) ;
x1 =0,8 x(-3)-0,6x4= -4,8 ; y1 =0,6x(-3)+0,8x
4=1,4. A1 ( -4,8
; 1,4) ;
x2 =0,8
x(-4,8)-0,6x1,4= -4,68 ; y2 =0,6x(-4,8)+0,8x 1,4= -1,76. A2
( -4,68 ; -1,76) ;
b.
Pour construire les points An ainsi obtenus, on écrit
l’algorithme suivant :
Variables :
i ,x, y, t : nombres réels
Initialisation :
x prend la valeur −3
y prend la valeur 4
Traitement :
Pour i allant de 0 à 20
Construire le point de coordonnées (x ; y)
t prend la valeur x
x prend la valeur 0,8x−0,6y
y prend la valeur 0,6t +0,8y.
Fin Pour
Recopier et compléter cet algorithme pour qu’il construise les points A0
à A20.
c. À l’aide d’un
tableur, on a obtenu le nuage de points suivant :
Identifier les points A0, A1 et A2.
Quel semble être l’ensemble auquel appartiennent les points An
pour tout n entier naturel ?
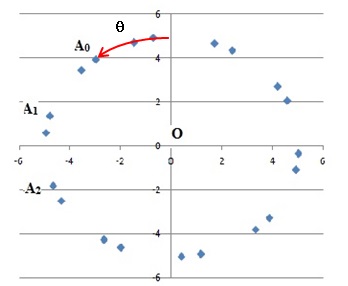
Les points semblent répartis sur un cercle de centre O et de rayon 5.
2. Le but de cette
question est de construire géométriquement les points An
pour tout n entier naturel.
Dans le plan complexe, on nomme, pour tout entier naturel n, zn
= xn +iyn l’affixe du point An.
a.
Soit un = |zn|. Montrer que, pour tout entier
naturel n, un = 5. Quelle interprétation géométrique peut-on faire
de ce résultat ?
un = (x2n +y2n)½
;
Démonstration par récurrence.
Initialisation
: z0 = (x20 +y20)½ =(16+9)½
= 5.
Hérédité : on suppose que up = (x2p +y2p)½ =5
up+1 = (x2p+1 +y2p+1)½ .
x2p+1 +y2p+1 =(
0,8xp −0,6yp)2+(0,6xp +0,8yp)2.
x2p+1 +y2p+1 =0,64xp2+0,36yp2-0,96xpyp+0,36xp2+0,64yp2-0,96xpyp=x2p +y2p .
La propriété est vrai au
rang p+1.
Conclusion
: la propriété est vraie au rang zéro et héréditaire.
Donc pour tout entier
naturel n, un = 5.
Les points An appartiennent au cercle de centre O et de
rayon 5.
b. On admet qu’il existe un réel θ
tel que cos(θ) = 0,8 et sin(θ) = 0,6.
Montrer que, pour tout
entier naturel n, eiθzn = zn+1.
eiθzn =(cos(θ)
+isin(θ))(xn+iyn)=xn cos(θ)-yn sin(θ)+
i(yn cos(θ)+xn sin(θ))
eiθzn
=0,8xn
-0,6yn +i(0,8yn +0,6xn )=xn+1 +iyn+1 = zn+1.
c. Démontrer
que, pour tout entier naturel n, zn = einθz0.
Démonstration par récurrence :
Initialisation
: z1 = =eiθz0 est vraie.
Hérédité :
on suppose que la propriété est vraie au rang p : zp
= eipθz0.
zp+1=eiθzp
=eiθ
eipθz0
=ei(p+1)θz0
; la propriété est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang zéro et héréditaire ;
donc pour tout entier
naturel n, zn = einθz0.
d. Montrer que θ+π/2
est un argument du
nombre complexe z0.
On note q0
l'argument de z0.
z0 / |z0| = cos q0+ i sinq0 = -0,6 +0,8 i.
Or -0,6 =- sin q=cos
( θ+π/2) et 0,8 =cos q=sin ( θ+π/2).
z0 / |z0| =cos (
θ+π/2) +i sin ( θ+π/2).
Par suite : q0= θ+π/2.
e. Pour tout entier naturel n,
déterminer, en fonction de n et θ, un argument du nombre complexe zn.
Représenter θ sur la
figure.
Expliquer, pour tout
entier naturel n, comment construire le point An+1 à partir du point An.
zn = einθz0
; arg(zn)
=nq +arg(z0)
=nq +θ+π/2
= (n+1)θ+π/2.
A partir du point An, on se déplace d'un angle q, sur le cercle de centre O
et de rayon 5. Utiliser un compas ou un rapporteur.
|
|
|
|
Asie.
Partie A : propriétés du nombre j= (-1+i3½) / 2
1. a. Résoudre dans
l’ensemble C des nombres complexes l’équation z2 +z +1 = 0.
Discriminant D = 12-4=-3=3i2.
Solutions : z1 =j= (-1+i3½) / 2 et (-1-i3½)
/ 2.
Le nombre complexe
j est une solution de cette équation.
2. Déterminer le
module et un argument du nombre complexe j, puis donner sa forme
exponentielle.
|j|=[(-1/2)2+(3½/2)2]½ =1 ;
arg (j) = q tel
que : cos q =
-0,5 et sin q = 3½
/ 2 ; q = 2p /3.
j = exp( 2ip /3).
3. Démontrer les
égalités suivantes :
a. j3 =
1 ;
j3 =exp( 2ip
/3 x3) = exp(2ip)
= 1.
b. j2 =
−1−j.
j2 =exp( 2ip
/3 x2)=exp( 4ip /3
)=cos(4p /3) +i
sin(4p /3) = (-1-i3½)
/ 2 =(-2+1-i3½) / 2 = -1-(-1+i3½) / 2=-1 -j.
4. On note P, Q, R
les images respectives des nombres complexes 1, j et j2 dans
le plan.
Quelle est la nature du triangle PQR? Justifier la réponse.
Affixe de P : 1 ; affixe de Q : (-1+i3½) / 2 ; affixe
de R : (-1-i3½) / 2 .
QP2=(1+0,5)2 +(0-3½ / 2 )2
= 9 / 4 + 3 / 4 = 3. QP = 3½.
RP2=(1+0,5)2 +(0+3½ / 2 )2
= 9 / 4 + 3 / 4 = 3. RP = 3½.
QR2=(-0,5+0,5)2 +(-3½ / 2 -3½
/ 2 )2 = 3. QR = 3½.
QP=RP=QR, le triangle PQR est équilatéral.
Partie B.
Soit a, b, c trois nombres complexes vérifiant l’égalité a +jb +j2c
= 0.
On note A, B, C les images respectives des nombres a, b, c dans le plan.
1. En utilisant la
question A - 3. b., démontrer l’égalité : a −c = j(c −b).
j2 = −1−j ; a+j b -c - jc = 0 ; a-c +j (b-c)=0 ; a-c =
j(c-b).
2. En déduire que
AC = BC
AC = |c-a| =|j| |c-b|;=|j| |c-b| ; or |j|=1 : AC = |c-b| ;
or BC =|c-b|. Donc AC=BC.
3. Démontrer
l’égalité : a −b = j2(b −c).
j2(b −c) = -(1+j)(b-c)= -(b-c) - j(b-c)= -(b-c) + (a-c)= a-b.
4. En déduire que
le triangle ABC est équilatéral.
|a −b| =| j2(b −c)| = |j2| |b-c|. Or |j2|
=1 ; |a −b| = |b-c| soit AB = BC.
Par suite AB = BC= AC, le triangle ABC est équilatéral.
|
|
Métropole.
1. Résoudre dans l’ensemble C des
nombres complexes l’équation (E) d’inconnue z :
z2 −8z +64 = 0.
Discriminant D =
(-8)2 -4 x64 =-3 x64 = -82x 3=
i282x 3 ; racine carrée de D : 8i 3½.
Solutions : z1 = (8+ 8i 3½) 2
= 4+4i3½ ; z2
= (8- 8i 3½) 2 = 4-4i3½.
Le plan complexe est muni d’un repère
orthonormé direct
2. On considère les
points A, B et C d’affixes respectives a = 4+4i3½, b = 4−4i3½
et c = 8i.
a. Calculer le
module et un argument du nombre a.
|a|=[42+(4 x3½)2 ]½=(16+48)½
= 8.
a = 8(0,5 +i3½ /2) ; cos q = 0,5 ; sin q = 3½
/2 ; arg(a) = q =
p/3.
b. Donner
la forme exponentielle des nombres a et b.
a = 8 exp(ip/3) ; b
= 8 exp(-ip/3).
|b|=[42+(-4 x3½)2
]½=(16+48)½ = 8.
b = 8(0,5 -i3½ /2) ; cos q'
= 0,5 ; sin q' = -3½
/2 ; arg(b) = q' = - p/3.
c.
Montrer que les points A, B et C sont sur un même cercle ce de centre O
dont on déterminera le rayon.
|c| = 8 ; arg (c) =p/2.
Les points A, B et C sont sur le cercle de centre O et de rayon R=8.
d. Placer les
points A, B et C dans le repère.
Pour la suite de l’exercice, on pourra s’aider de la figure de la
question 2. d. complétée au fur et à mesure de l’avancement des
questions.
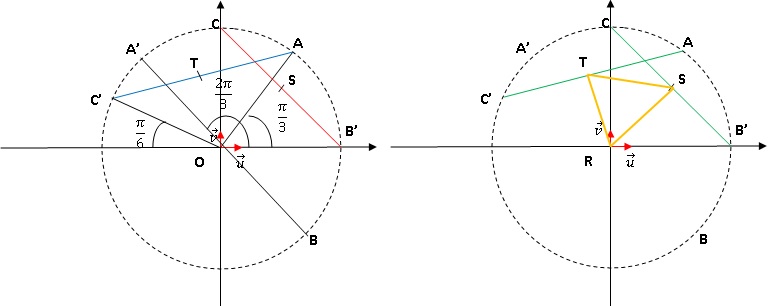
3. On considère
les points A′, B′ et C′ d’affixes respectives a′ = a exp(iπ/3), b′ = b
exp(iπ/3) et c′ = c exp(iπ/3)..
a. Montrer que b′ =
8.
b'=8 exp(-ip/3) x exp(iπ/3)
= 8 exp(i(-p/3+p/3) = 8 exp (0i) = 8.
b.
Calculer le module et un argument du nombre a′.
a' = 8 exp(ip/3) x
exp(iπ/3) = 8 exp(i(+p/3+p/3) = 8 exp (2ip/3)
; |a'| =8 ; arg(a')= 2p/3.
Pour la suite on admet que a′ = −4+4i x3½
et c′ = −4 x3½+4i.
4. On admet que si
M et N sont deux points du plan d’affixes respectives m et n alors le
milieu I du segment [MN] a pour affixe (m+n) /2 et la longueur MN
est égale à |n −m|.
a. On note r, s et
t les affixes des milieux respectifs R, S et T des segments [A′B],
[B′C] et [C′A].
Calculer r et s. On admet que t = 2−2x3½+i(2+2x3½).
Affixe de A' : −4+4i x3½
; affixe de B: 4−4ix3½
; affixe de R : r =(-(4+4 /2 +4i x3½ -4i
x3½ ) /2=0.
R est confondu avec l'origine O.
Affixe de B' : 8
; affixe de C : 8i
; affixe de S : s = 8 /2 +8i / 2
=4 +4i.
b.
Quelle conjecture peut-on faire quant à la nature du triangle RST?
Justifier ce résultat.
RS = OS =|s|= (42+42)½ =4 x2½.
RT =OT =| t| = [(2−2x3½)2+(2+2x3½)2]½
=4 x2½.
ST2 =(2−2x3½-4)2
+(2+2x3½-4)2
=(-2−2x3½)2
+(-2+2x3½)2
=16 ; ST = 4 x2½.
RS=RT=ST, le triangle RST est équilatéral.
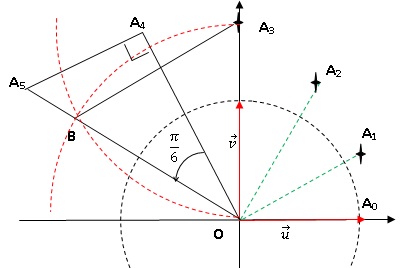
Nlle Calédonie mars 2016.
On considère les nombres complexes zn définis, pour tout
entier naturel n, par
z0 = 1 et zn+1 =(1+i 3½/3)zn.
On note An le point d’affixe zn dans le repère
orthonormé.
L’objet de cet exercice est d’étudier la construction des points An.
1. a. Vérifier que
1+i 3½/3=2 / 3½ exp(ip/6).
Module de z=1+i
3½/3 : |z|=(1+3 / 9)½ = 2 / 3½ = 2 x3½
/3.
z /|z|=
cos q +isin q
avec cos q
= 3½ /2
et sin q
= 0,5 soit q =p/6.
b. En déduire z1 et z2
sous forme exponentielle.
z1=(1+i 3½/3)z0 =1+i
3½/3 =2 / 3½
exp(ip/6).
z2=(1+i
3½/3)z1 =2
/ 3½ exp(ip/6)
x 2
/ 3½ exp(ip/6))
=4 /3 exp(ip/3).
2. a.
Montrer que pour tout entier naturel n,
zn =[2
/ 3½ ]n exp(inp/6).
Démonstration par récurrence :
Initialisation
: z1=2
/ 3½ exp(ip/6).
La propriété est vraie au rang 1.
Hérédité :
on suppose que zp =[2
/ 3½ ]p exp(ipp/6)
est vrai.
zp+1 = [2
/ 3½ ]p exp(ipp/6)
x 2 / 3½ exp(ip/6) = [2
/ 3½ ]p+1 exp(i(p+1)p/6).
la propriété est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire.
Donc, pour tout entier naturel n, zn
=[2 / 3½ ]n
exp(inp/6).
b.
Pour quelles valeurs de n, les points O, A0 et An
sont-ils alignés ?
O et A0 sont sur l'axe des
réels, donc le point cherché est également sur cet axe.
np/6 = p soit n = 6 ou un multiple
de 6.
3. Pour tout entier naturel n, on
pose dn = |zn+1 −zn|.
a. Interpréter
géométriquement dn.
dn = An+1An, distance des points An+1
et An.
b. Calculer d0.
z1-z0=(1+i 3½/3)z0
-z0=i 3½/3 z0=i
3½/3 ; d0 = 3½/3.
c.
Montrer que pour tout entier naturel n non nul, zn+2-zn+1=(1+i
3½/3)(zn+1-zn).
Démonstration par récurrence :
Initialisation
: z2-z1=(1+i
3½/3)z1 -z1=(1+i
3½/3)z1 -(1+i
3½/3)z0 =(1+i
3½/3)(z1-z0).
La propriété est vraie au rang 2.
Hérédité :
on suppose que zp+2-zp+1=(1+i
3½/3)(zp+1-zp)
est vrai.
zp+3-zp+2=(1+i
3½/3)zp+2 -zp+2=(1+i
3½/3)zp+2 -(1+i
3½/3)zp+1 =(1+i
3½/3)(zp+2-zp+1).
La propriété est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang 2 et héréditaire.
Donc, pour tout entier naturel n,
non nul, zn+2-zn+1=(1+i
3½/3)(zn+1-zn).
d.
En déduire que la suite (dn)n>0 est
géométrique puis que pour tout entier naturel n, dn =3½
/3 (2 / 3½)n.
dn+1 =| zn+2-zn+1|
; dn =|zn+1-zn|.
dn+1 =|1+i
3½/3 |dn ; dn+1
=2/ 3½
dn ;
La suite est géométrique de premier terme d0
= 3½/3
et de raison q = 2/
3½.
4. a.
Montrer que pour tout entier naturel n, |zn+1|2 =
|zn|2 +d2n.
|zn+1| =[2
/ 3½ ]n+1 ;
|zn+1|2 =[2 / 3½ ]2n+2
= =[2
/ 3½ ]2n x[2
/ 3½ ]2=[2
/ 3½ ]2n x4 /3.
|zn+1|2 =
|zn|2
x4 /3 et d2n
=1 /3 (2 / 3½)2n.
|zn|
=[2
/ 3½ ]n ;
|zn|2 =[2 / 3½ ]2n
;
|zn|2
+d2n
=[2 / 3½ ]2n
+1 /3 (2 / 3½)2n
= [2
/ 3½ ]2n (1+1/3) =
[2
/ 3½ ]2n x4 /3 =
|zn+1|2 .
b. En déduire que, pour tout entier
naturel n, le triangle OAn An+1 est rectangle en An
|zn+1|
=OAn+1 ; |zn|
=OAn ; dn = An+1An.
|zn+1|2 = |zn|2
+d2n conduit à : OA2n+1 =
OA2n
+An+1An 2.
D'après la
rééciproque du théorème de Pythagore, le triangle OAn An+1
est rectangle en An
c.
Construire, à la règle non graduée et au compas, le point A5.
d. Justifier cette
construction.
Le triangle OA4
A5 est rectangle en A4. Le point A5
appartient à la droite D perpendiculaire à (OA4) passant par
A4.
arg(z5) = 5p/6
; arg(z3)=3p/6 ; donc l'angle formé
entre les vecteurs OA3 et OA5 mesure p/3.
Tracer le triangle équilatéral OA3B.
|
|